Differentiable Scaffolding Tree for Molecule Optimization（论文解读）

  Differentiable Scaffolding Tree for Molecule Optimization（ICLR 2022）

可微分骨架树：基于梯度的分子优化算法

paper：Differentiable Scaffolding Tree for Molecule Optimization | Papers With Code

code：GitHub - futianfan/DST: (differentiable) gradient-based optimization on a chemical graph for de novo molecule design/optimization (ICLR 2022)

---

Abstract

 Deep generative models and combinatorial optimization methods achieve initial success but still struggle with directly modeling discrete chemical structures and often heavily rely on brute-force enumeration. The challenge comes from the discrete and non-differentiable nature of molecule structures. To address this, we propose differentiable scaffolding tree (DST) that utilizes a learned knowledge network to convert discrete chemical structures to locally differentiable ones. DST enables a gradient-based optimization on a chemical graph structure by back-propagating the derivatives from the target properties through a graph neural network (GNN). Our empirical studies show the gradient-based molecular optimizations are both effective and sample efficient. Furthermore, the learned graph parameters can also provide an explanation that helps domain experts understand the model output. 深度生成模型和组合优化方法取得了初步成功，但仍然难以直接模拟离散的化学结构，并且通常严重依赖于强力枚举。挑战来自分子结构的离散性和不可微性。为了解决这个问题，我们提出了可微分支架树(DST ),它利用一个学习到的知识网络将离散的化学结构转化为局部可微分的结构。DST通过图形神经网络(GNN)反向传播目标属性的导数，实现了化学图形结构的基于梯度的优化。我们的实证研究表明，基于梯度的分子优化是有效的和样品高效的。此外，学习到的图形参数还可以提供帮助领域专家理解模型输出的解释。

---

思路：基于梯度的分子优化

在药物发现中，分子优化（即找到具有理想性质的分子结构，是核心的一步）。最近深度学习的发展确实提供了一些新的思路，但目前大部分依赖图生成算法的分子优化都是通过图神经网络（graph neural network, GNN）来显式地生成一个分子，然后优化目标函数，通过反向传播梯度来更新GNN参数，使得网络生成具有优化性质的分子。例如在增强学习（reinforcement learning, RL）中目标函数是根据反馈（reward）定义的；在深度生成模型（deep generative model, DGM）中基于和目标分子的广义距离定义。但这些算法普遍优化能力不够强，尤其没有考虑oracle的成本，许多算法需要调用数十万甚至百万次oracle才能得到较好的结果，而这在实际分子设计过程中显然是不现实的。

我们知道，数值优化的核心就是在一个点估计其指向极值点的方向，而这一方向一般可以通过梯度估计。那我们是否可以估计一个分子的性质相对于结构的梯度？通过这个梯度估计方向进而优化一个分子？在Alan Aspuru-Guzik组的Deep Molecular Dreaming[2]一文中作者利用分子的字符串（SELFIES）表示实现了这一点：将分子看做每个位置字符的分布概率，通过一个一维卷积神经网络（convolutional neural network, CNN）学习其性质，得到可微的性质预测器，进而估计分子的梯度，但是效果并不好。而在本文中，作者通过提出分子的可微分骨架树（Differentiable Scaffolding Tree, DST）这一概念，使得分子直接在结构层面上可微，进而构建了一个高效的优化算法。与其他生成模型不同，作者先预训练(pre-train)了一个以骨架树（ST）为输入的GNN来预测性质（标量）。然后在优化过程中固定GNN参数，每步迭代里首先构造分子相应的DST，通过前向传播用GNN来预测性质，然后优化目标性质并通过反向传播梯度来更新DST里的参数，进而优化分子结构。

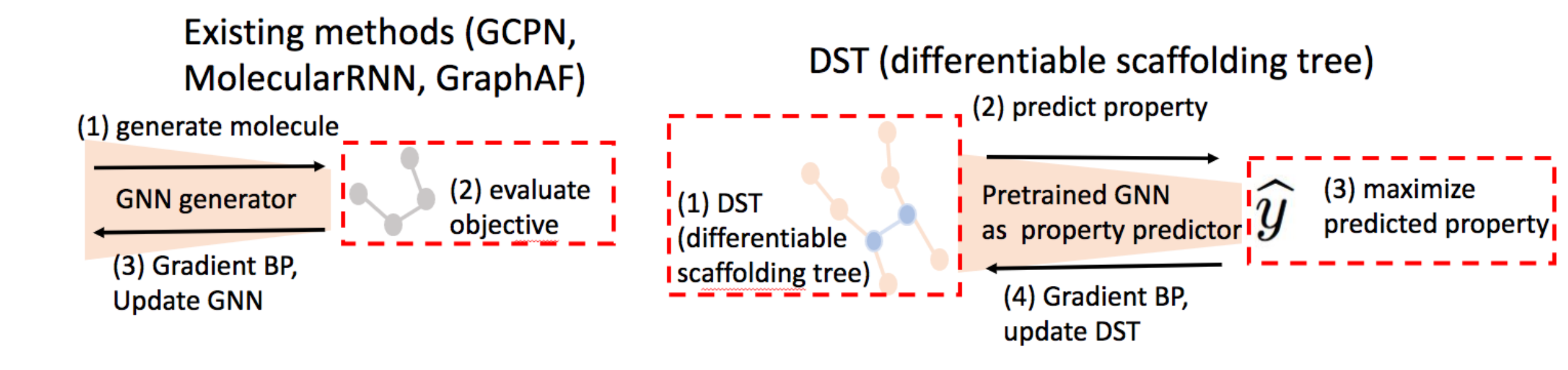
Figure 5: Left: Most of the existing methods (including GCPN (You et al., 2018), Molecular RNN (Popova et al., 2019), GraphAF (Shi et al., 2020)) use GNN as a graph generator. 
==> (1) generate molecule;
==> (2) evaluate learning objective (loss in deep generative model or reward in reinforcement learning); 
==> (3) back-propagate (BP) gradient to update GNN.
In sum, the learning objective is differentiable w.r.t. the GNN’s parameters.

Right: Regarding DST, given the pretrained GNN as surrogate oracle model (i.e., property predictor), we have several steps:
 ==> (1) construct differentiable scaffolding tree (DST);
 ==> (2) predict the property via GNN;
 ==> (3) maximize the predicted property yˆ (learning objective，yˆ 是一个标量);
 ==> (4) back-propagate (BP) gradient to update DST.
In sum, the learning objective is differentiable w.r.t. DST (also input of GNN).

Summary: DST makes the learning objective differentiable w.r.t molecule graph structure, while prior works make the learning objective differentiable w.r.t. neural networks’ parameters. Our approach directly optimizes molecular graph structures, while prior works indirectly search for the molecule graphs with the help of a neural network.

分子的可微分骨架树

首先我们明确本文关注从头分子优化（de novo molecule optimization），即以一个优化算法在一个隐式定义的小分子空间上找到性质较好的分子。而分子性质由一个Oracle给出，即给定一个分子，输出相对应的性质，可以看作一个黑盒函数（black box function of molecules），例如衡量一个分子的类药性的QED（QED（quantitative estimate of drug-likeness）是一种将药物相似性量化为介于0和1之间的数值的方法）。

为了使分子在图结构层面上可微，首先需要扩展分子图的概念。另外为了避免生成环的中间步骤可能带来的不必要的麻烦，作者选择在优化过程中用骨架树（scaffolding tree, ST）来表示分子，其节点定义为一个基本单位（substructure），包含了常见的原子和单环（详见原文附录Figure 5）。我们可以用节点的类别矩阵（node indicator matrix）和节点之间的链接矩阵（adjacency matrix）表示一个骨架树。其中类别矩阵每一行是一个one-hot向量，代表了该节点是哪一个基本单位，而链接矩阵中的每一个元素都是binary的数字，指示每一对节点之间是否连接。

构造可微分骨架树（DST）的核心是将节点的类别和连接看做可学习的0到1的概率分布，而非0或1的binary code。其中为了实现连接可微性的自洽，作者提出了与连接等价的权重向量（node weight vector），通过一个节点的权重表示其存在与否，并通过权重构造连接矩阵，将连接与否的问题变成了该节点是否存在的问题：

从骨架树得到可微分骨架树的方法如下所示： 
==> 首先将分子结构抽象为骨架树,
==> 然后将骨架树中每个结点连接上一个拓展节点（expansion node）
==> 每一个叶结点和拓展结点的权重（结点权重是一个sigmoid的输出，保证在0-1之间）和类别（节点类别是一个softmax的输出，保证和为1）是可学习的（learnable）。

类梯度上升的优化算法

为了进行优化，作者首先预先训练（pre-train）了一个GNN来做性质预测，其输入是一个分子的可微分骨架树，输出是目标的性质 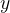（标量），即 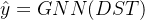，为了平衡不同权重节点的贡献，作者在GNN中使用了加权平均的read-out方法：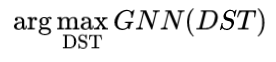

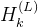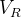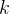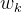其中  代表第  回迭代之后的节点特征（node embedding）的第  行， 代表第 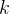 个节点的权重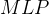， 代表全连接网络。整个算法是一个迭代式优化。在单步迭代中，给定输入分子的DST，得到了可微的性质预测替代后，可以通过任意梯度优化算法（文中使用了Adam）解：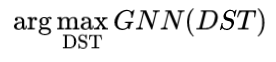

 来得到优化后的DST。在得到优化后的DST后，根据其优化后的权重和类别，作者设计了如下三种在对应骨架树上的操作：（1）删除（SHRINK）叶结点权重小时，意味着该节点对性质提升没有帮助，或者说该节点的存在对性质提升有负面影响，所以在对应骨架树上删除该节点。（2）拓展（EXPAND）拓展节点权重大时，意味着该节点的存在对性质提升帮助是正向的，所以在对应骨架树上加上一个新的结点。该节点的类别也从对应softmax输出值中选择。（3）替换（REPLACE）若一个节点权重改变不大，但类别改变较大时，不删除也不拓展，但是在优化后的分布中重新采样一个substructure（softmax输出中值比较大的）。

​Figure 1: : During inference, we construct the corresponding scaffolding tree and differentiable scaffolding tree (DST) for each molecule. We optimize each DST along its gradient back-propagated from the GNN and sample scaffolding trees from the optimized DST. After that, we assemble trees into molecules and diversify them for the next iteration.

优化算法中的一步迭代。

根据更新后的DST采样其中一个操作，得到对应的骨架树作为下一轮迭代的输入，如此我们迭代地优化分子。在每一轮迭代内DST的维数是固定的，由输入分子决定，因此一轮迭代只能得到和原分子相差最多一个节点的分子。但在多轮迭代优化过程中，每一轮的输入都是上一轮的输出，因此相应的DST维度也会变化，使得生成分子的大小只受限于优化迭代次数。

在得到优化后的骨架树后，作者枚举对应的所有可能的分子图，用oracle测量每一个分子。为了有更好的优化效果，并兼具输出分子的多样性，作者每次优化时同时优化多条轨迹，并在其中使用determinantal point process（DPP）来选择保留的分子。即在每一部枚举出对应的多个可能的分子图之后，不是单纯根据性质好坏，而额外考虑了相似性矩阵的行列式，即选择最大化下式的一批分子：

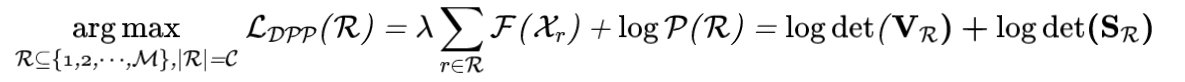
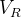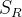 其中  是subset  这批分子的性质分数的对角矩阵，而  则是这批分子的相似性矩阵。可以注意到单纯依据  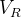的行列式挑选就是greedy的top-k选择。而相似矩阵的行列式的最大化则鼓励subset内的diversity的增加（可以考虑一个 2*2 的例子，对角线为1，非对角为彼此之间的相似度）。如此我们便得到了一个完整的优化算法。

优化效果测试

作者首先衡量主要的优化效果，包含了单目标优化和多目标优化（同时优化多个性质）。为了能够有比较全面的对比，所有算法选择了分数最高的100个分子衡量其：

• 新颖性（Nov）：生成分子不在训练集（如果有）中的比例；

• 多样性（Div）：生成分子的多样性，衡量对化学空间的探索能力；

• 目标性质的平均优化结果（APS）；

• Oracle调用的次数（#oracle）：我们关注有限的oracle调用的情况下的表现，因为oracle调用的数量是衡量一个算法效率的重要指标；

由于DST和一些其他算法的一部分oracle调用可以离线完成（比如利用已有的标注数据），另一部分必须线上完成，所以#oracle是A+B的形式，A为线下调用，B为线上调用。

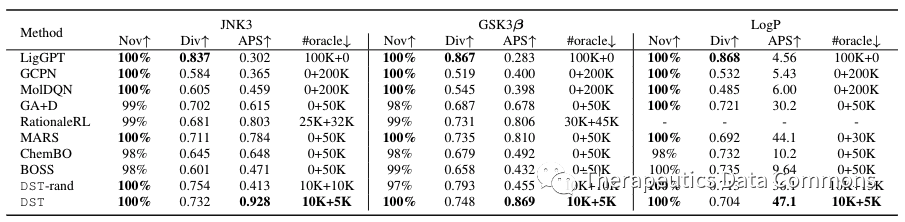
单目标优化结果。

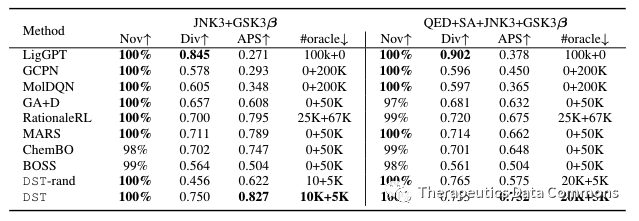
多目标优化结果。

从实验结果上看，直接运用了梯度信息的DST优化效率最高，说明了由DST估计的梯度的可靠性。深度生成模型（LigGPT）由于其本身并不是一个迭代优化算法，表现并不好。增强学习方法（GCPN／MolDQN）虽然在无限oracle调用的情况下能够得到一些较好的结果，但是不出所料在限制oracle调用的情况下表现相对不好。而以传统的组合优化方法为基础的算法（如GA+D，MARS）表现相对还是更好。

为了更系统地比较算法效率，作者测试了算法的oracle efficiency，即不同方法在不同oracle调用次数下的优化性能。结果如下：

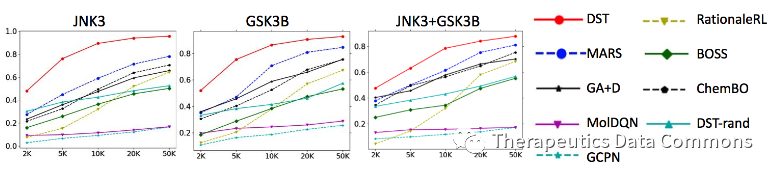
Oracle efficiency测试结果。其中DST-rand为DST的ablation study，即同样设定下每步随机选择骨架树上的操作。

横轴为oracle调用数量，纵轴为top-100个分子的平均性质（越高越好）。DST在三个任务上都取得了最好的效果，其他结论也和第一个实验类似。

由可微性得到的可解释性

作者另外展示了由DST带来的分子性质的可解释性。通过观察当前DST对各个结点权重和梯度，我们可以看到不同的结点对性质提升的影响，进而分析不同基团、亚结构对性质的影响。

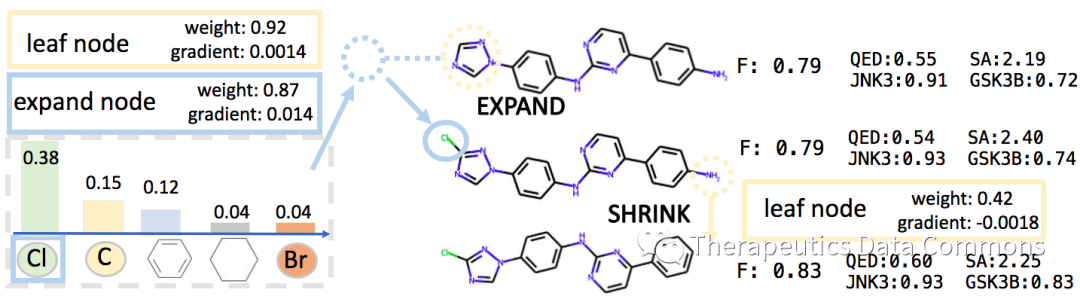
分子可解释性实例。

---

未完..，还需要整理

参考资料

[1] Fu, T., Gao, W., Xiao, C., Yasonik, J., Coley, C. W., & Sun, J. (2021). Differentiable scaffolding tree for molecular optimization. arXiv preprint arXiv:2109.10469.

[2] Shen, C., Krenn, M., Eppel, S., & Aspuru-Guzik, A. (2021). Deep Molecular Dreaming: Inverse machine learning for de-novo molecular design and interpretability with surjective representations. Machine Learning: Science and Technology, 2(3), 03LT02.

可微分骨架树：基于梯度的分子优化算法