猿创征文丨赶紧进来修内功!!! 详细讲解数据在内存中的存储(浮点数篇)

本文介绍了浮点型家族各类型的特点 .浮点数与二进制数之间的转换.为什么浮点数会存在精度损失.浮点数在内存中的存储规则.从内存中取出浮点数的规则.以及相应代码练习.

一.浮点数家族

float
double
long double
常见的浮点数:3.14.159 1E10

1.float类型

float为单精度浮点型 类型长度四字节 保留7位有效数字 输出数据用%f第七位数字后面的会发生精度偏失,第七位数字后面的数据一般会四舍五入给第七位数据然后为无效数字但默认会显示显示6位小数位

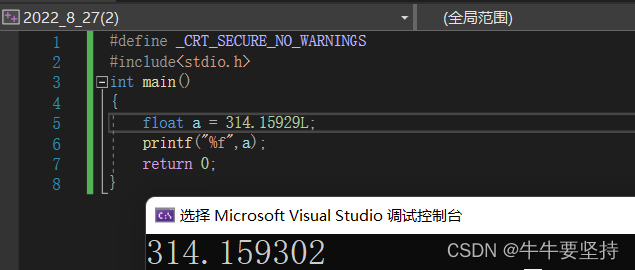
314.15929最后输出成了314.159302可以看到一个单精度浮点型数据最后打印出来是保留六位小数,并且是只有7位有效数字,从整数到小数前7位是有效的后面的数会当成精度位四舍五入到第七位数字.七位数字后面的为精度偏失的无效数据

2.double类型

double为双精度浮点型类型长度八字节 保留16位有效数字 输出数据用%lf第十六位数字后面可能精度偏失会四舍五入到第十六位数字,默认显示前6位小数

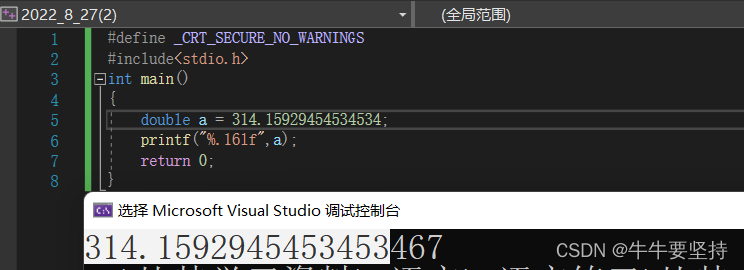
如果正常%lf打印则会保留前六位数字第六位会被后面数据四舍五入进位,但测试double保留十六位有效数字 此时用%.16f 最后显示出的前十六位数据都是有效的,而后面的则是偏失的精度位.

3.long double类型

long double类型 和double类型长度一样是八个字节,输出数据用%llf输出的数据和double也一样也 都会发生精度偏失.

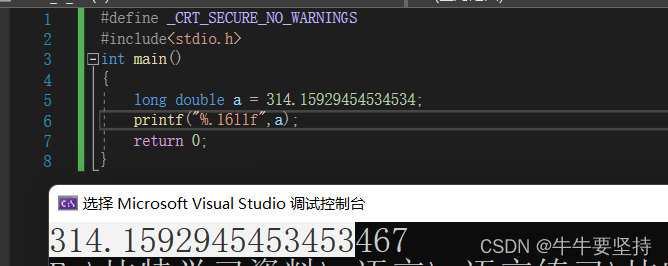
二.为什么浮点数有精度损失?

上图中都可以看到浮点数最后都会出现无效数字,这些数字也可以被称为精度损失的位数 ,那浮点数为什么会有精度损失呢?

1.浮点数和二进制数之间的转换

这里说的浮点数指的整数部位和小数部位都是十进制的数,在这篇博客中讲到了整数进制数间的转换方法->整数进制数间的转换
而浮点数和二进制间的转换和整数有些不同,整数部分和正常整数转换是一样的,但是小数部分不一样.

①浮点数转二进制数

2.5是一个浮点数,整数部分是2,小数部位分是0.5
整数部分转换为二进制数先按除二倒取余数法得到二进制数为10

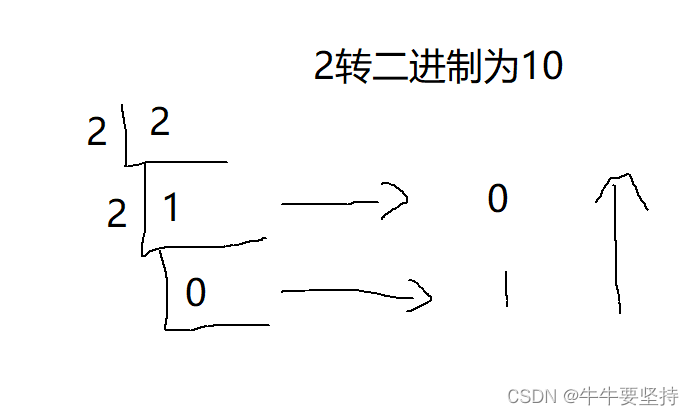
而0.5小数部分用乘二顺取整数法
0.5乘2得到1.0 取掉整数后式子为0.0乘任何数都为0此时结束得到数字1

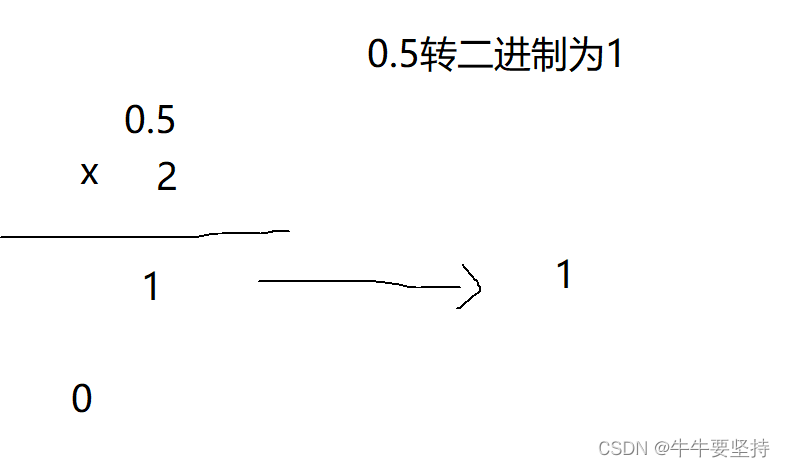
最后得到的2.5十进制数转换成的二进制数为10.1

当然小数部分此时就存在一个问题,一直乘取出整数后最后式子都不为0怎么办?

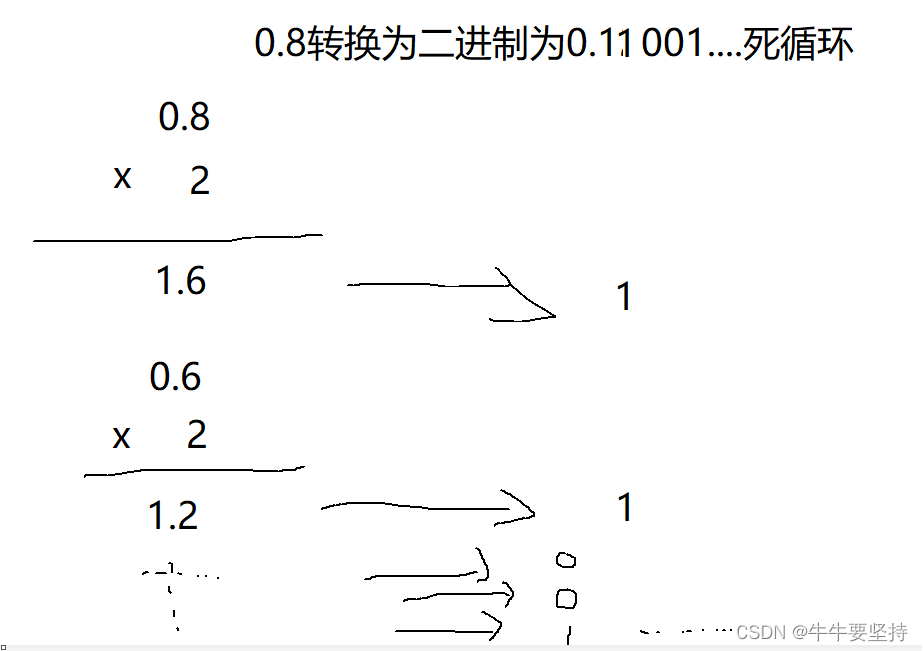
小数部位采用这个方法转换为二进制数得到的数可能会发生死循环或者得到的二进制数数是无穷的,这个问题是无法避免的, 一般会规定保留指定位数的小数 ,但是不管怎样保留最后还原回去是得不到之前的结果的,这里做了些特殊的处理,最后得到的数会是和原来的数一样,但是在后面很多位小数后会出现偏失的精度数.比如1,1最后可能在计算机中取出会是1.1000000000000000000001最后的1为精度损失,最后会进行一些处理使得显示的时候最会有1.100000 实际上在后面的位里可能有不准确的位数.
这也正是计算机中存储浮点数最后会发生精度损失的原因!!!

②二进制数转浮点数

10.1这个二进制数又是怎样转换回0.5的呢?
整数部分仍然使用按位权展开方程式之和
二进制数个位数位权为2的0次方 十位为2的1次方以此类推
每一位的数与它位权相乘然后相加得到整数部分十进制2

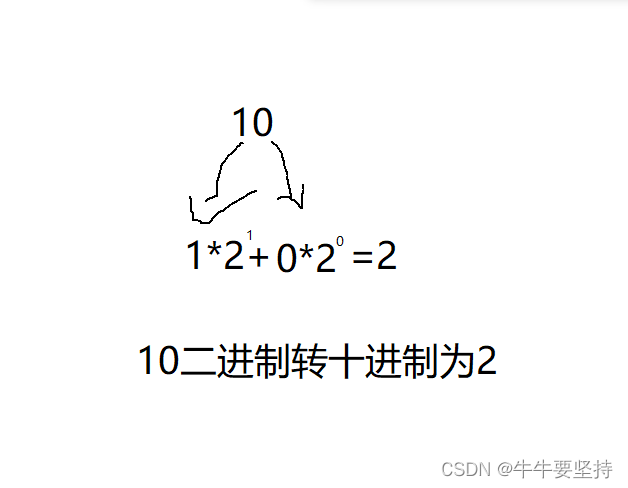
小数部分1也采用按位权展开方程式之和
二进制小数部分第一位位权为2的-1次方第二位为2的-2次方以此类推
每一位与它对应的位权相乘然后相加得到小数部分十进制0.5

最后二进制10.1转换为十进制为2.5

思考:
那如果是0.8这样的数转换为二进制数后会是一个无限循环的二进制数0.1100112001…,尽管保留后面指定小数位数,最后按位权展开方程式之和得到的是0.750…后面是一些很小的精度位数
取出来而又是怎么得到0.8这个数字的呢?
因为得出来的浮点数二进制形式存放在计算机内部转换时浮点数有自己一套存储规则…

三.浮点数在计算机内部存储规则

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：
(-1)^S * M * 2^E
(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位

1.举例分析浮点数存储规则

上面分析了2.5这个十进制数转换为二进制数为10.1
根据上面的存储规则10.1是整数S表示符号位,正数为0
表示M有效数字将10.1可以等价转化为1.01*(2^1) 此时1.01在M这个范围 表示有效数字
2^E 指数位对应的就是2^1 E也就是1
10.1这个二进制数根据规则S为0 M为1.01 E为1 转换为了(-1)^0*(1.01)*(2 ^ 1)

2.浮点数(float)在内存里的存储

整数转换为二进制数内存中源码转反码转补码方式
而浮点数在内存中转换为二进制数的存储方式是根据其存储规则IEEE 754规定:
对于32位浮点数(float),4个内存单元有32位空间
最高一位放符号位S,接着的八位放指数E,剩下的23位放有效数字M

3.浮点数(double)在内存里的存储

double为双精度浮点型类型大小八字节,精度更高意味着有效数字更多,上面也说到double类型可以保留十六位有效数字
对于64位浮点数(double)8个内存单元有64位空间
最高一位放符号位S,后面接着11位放指数E,最后52位存放有效数字

4.IEEE 754存储规则特别规定

IEEE 754对有效数字M和指数E，还有一些特别规定。
前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。
IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的
xxxxxx部分。

至于指数E，情况就比较复杂。
首先，E为一个无符号整数（unsigned int）
这意味着，如果E为8位，它的取值范围为0 ~ 255；如果E为11位，它的取值范围为0~2047。但是，我们
知道，科学计数法中的E是可以出现负数的，而负数又要用占用符号位,但E是无符号整数
所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数比如，2^1的E是1，所以保存成32位浮点数时，必须保存成1+127=128，即10000000。
是127；
而对于11位的E，这个中间数是1023。

5.浮点数从内存中取出的规定

上面说到存M时会去掉有效数字整数部分的1存小数部分,而取出来时需要再加上这个1
比如保存1.01的时候，只保存0100000000，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。
以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字
而64位浮点数有效数字是1.xxxxxxxx将1舍去xxxxxxx放在最后52个空间,取出来时再把1加上就等于保存了53位有效数字

然后，指数E从内存中取出还可以再分成三种情况(以32位float浮点数为例)：
E不全为0或不全为1
这时，浮点数就采用下面的规则表示，即指数E的计算值减去中间值 127（或1023），得到真实值，再将
有效数字M前加上第一位的1。
比如：
0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为
1.0*2^(-1)，其阶码为-1+127=126，表示为
01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000，则其二进
制表示形式为:0 01111110 00000000000000000000000
取出来时126减去中间值得到E为-1 M取出来加上去掉的1为1.0000000…S为0表示正
最后得到1.0000…*2(-1)得到取出来的二进制数0.1转换为十进制数为0.5

E全为0 当这8位的序列都为0时表示实际上存进去的E为-127
这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于
0的很小的数字。
以32位浮点数为例:当E为0根据规则取出来E为-126,此时不管你有效数字为多少,最后提取出来是一个1.xxxx*(2^-126)是一个非常小的数字,这个数字已经是接近0了,也就是此时取出来不用把这个去掉的1加上直接表示0.xxxx*(2 ^ -126)表示±0是一个接近 于0的数,后面xxxx就相当于是精度位可以忽略

E全为1 这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；
以32位浮点数为例:当E表示的八位全是1取出来为255,想象一下1^(2 ^255)是一个多大的数,此时M后面那些有效数字都可以表示为0, 因为E指数特别大,取出来后这个数已经可以表示是±无穷大了,那些精度数字也可以省略

四.代码练习

学了整形转二进制存储在内存中,浮点数转二进制数存储在内存中,接下来学以致用,来做做题吧
思考:浮点数在内存中二进制数和整数在内存中二进制数都是遵循大小端存储方式吗?

1.求代码运行结果

int main()
{
int n = 9;
float *pFloat = (float *)&n;
printf("n的值为：%d\n",n);
printf("*pFloat的值为：%f\n",*pFloat);
*pFloat = 9.0;
printf("num的值为：%d\n",n);
printf("*pFloat的值为：%f\n",*pFloat);
return 0;
}
1
2
3
4
5
6
7
8
9
10
11

最后的输出结果↓↓↓

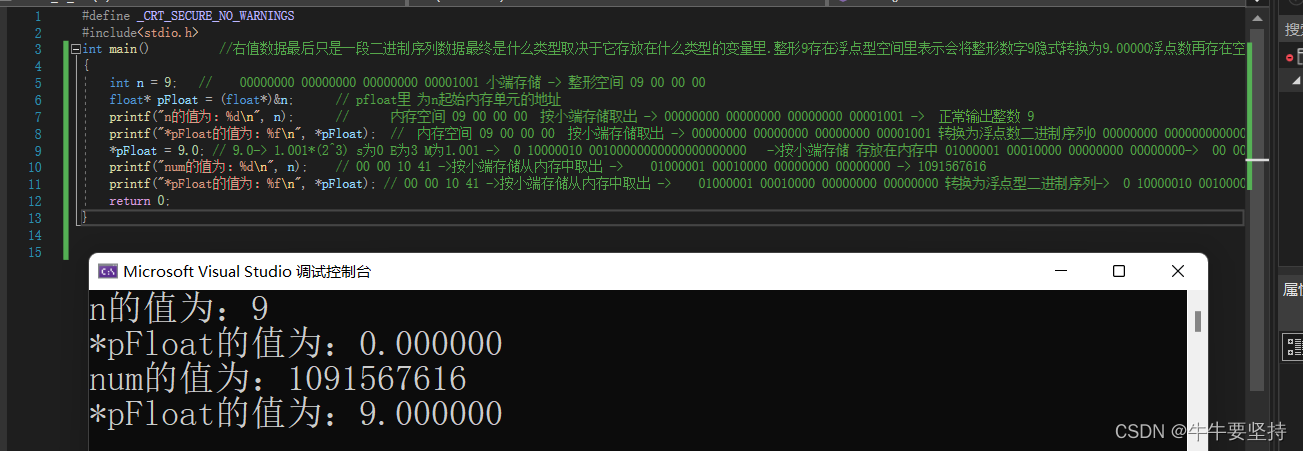
2.分析程序输出的结果

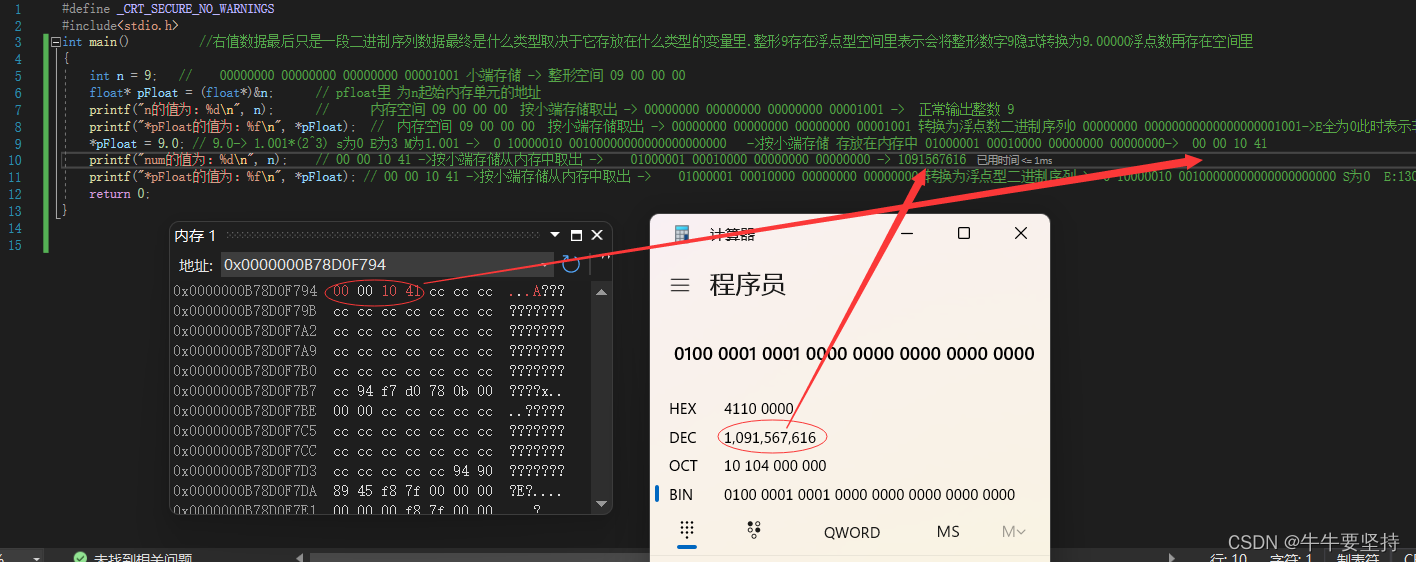
通过一步步调试和计算得出,浮点数按IEEE 754规则转换为二进制数后在内存里仍然遵循大小端存储方式,(按每个字节为单位,低位上的内容放低地址处的内存单元…)
最后取出来的时候按存进去时候的规律得到原来数字.再根据对应的数据类型处理取出来的这串二进制序列

#include
int main()          //右值数据最后只是一段二进制序列数据最终是什么类型取决于它存放在什么类型的变量里.整形9存在浮点型空间里表示会将整形数字9隐式转换为9.00000浮点数再存在空间里
{
	int n = 9;   //    00000000 00000000 00000000 00001001 小端存储 -> 整形空间 09 00 00 00
	float* pFloat = (float*)&n;      // pfloat里 为n起始内存单元的地址
	printf("n的值为：%d\n", n);      //      内存空间 09 00 00 00  按小端存储取出 -> 00000000 00000000 00000000 00001001 ->  正常输出整数 9 
	printf("*pFloat的值为：%f\n", *pFloat);  //  内存空间 09 00 00 00  按小端存储取出 -> 00000000 00000000 00000000 00001001 转换为浮点数二进制序列0 00000000 00000000000000000001001->E全为0此时表示非常小的数 接近于0 保留前面6位小数得到0.000000
	*pFloat = 9.0; // 9.0-> 1.001*(2^3) s为0 E为3 M为1.001 ->  0 10000010 00100000000000000000000   ->按小端存储 存放在内存中 01000001 00010000 00000000 00000000->  00 00 10 41
	printf("num的值为：%d\n", n);    // 00 00 10 41 ->按小端存储从内存中取出 ->    01000001 00010000 00000000 00000000 -> 1091567616
	printf("*pFloat的值为：%f\n", *pFloat); // 00 00 10 41 ->按小端存储从内存中取出 ->    01000001 00010000 00000000 00000000 转换为浮点型二进制序列->  0 10000010 00100000000000000000000 S为0  E:130-127为3 M为1.001.....-> 1.00100000000...*(2^3) ->9.000000
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12

五.浮点数存储总结

浮点数转换为二进制数整数部分采取除二倒取余数法,小数部分采取乘二取整法
最后再根据存储标准IEEE 754 转换为对应的二进制序列放在内存中,然后在内存中存放在对应的内存单元里时.这个二进制序列又会遵循大小端存储方式每个内存单元存放8位数据(2个十六进制)
最后取出来时又会按照原来存进去的规律取出然后根据二进制序列是什么类型再根据对应类型从内存中转换出来得到最终的结果!!!

计算机做这个工作仅需要很少很少的时间就能得出结果,而我们分析这个运算过程却要很多时间
但是,只有我们了解计算机存储工作原理,把内功练好,编程技术自然就上去了~~

写文不易,给个一键三连支持下吧~~~