-
机器学习吴恩达
高偏差/欠拟合的情况下,增加数据到训练集不一定能有帮助
解决高方差:
- 获取更多的训练实例
- 尝试减少特征的数量
- 尝试增加正则化程度lambda
解决高偏差:
- 尝试获取更多的特征
- 尝试增加多项式特征
- 尝试减少正则化程度lambda
把数据分为训练集,交叉验证集和测试集,针对不同隐藏层层数的神经网络训练升级网络,然后选择交叉验证集代价最小的神经网络
类偏斜的误差度量
类偏斜:即训练集中有非常多的同一种类实例,只有很少或没有其他类的实例。(故:不可用误差的大小来评判算法效果)
引出查准率precision 和 查全率 recall
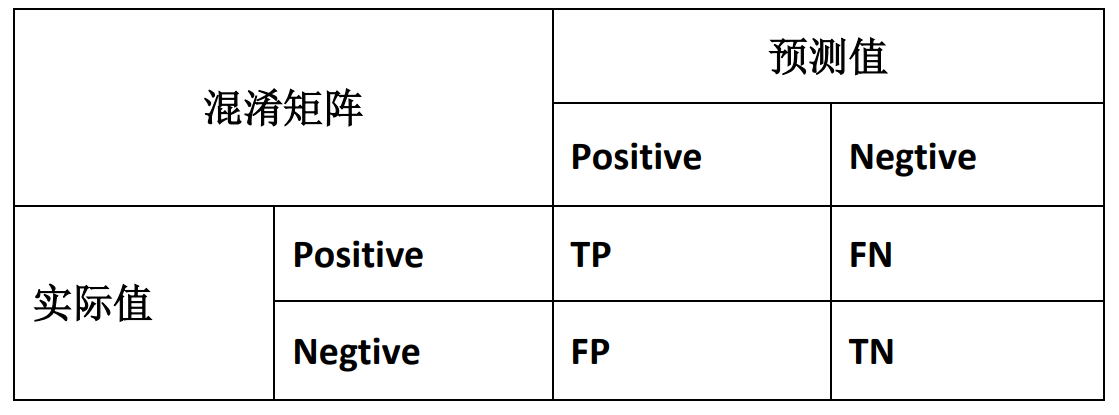
查准率precision = TP/(TP+FP)
查全率recall = TP/(TP+FN)P-R曲线图会根据阈值的不同而变化
选择阈值的方法:F1 Score
F1 Score = 2 P R / ( P + R ) 2PR/(P+R) 2PR/(P+R) 我们选择使得F1 Score值最高的阈值逻辑回归函数的代价函数:
h θ ( x ) = 1 1 + e − θ T X h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} X}} hθ(x)=1+e−θTX1
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们
也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将 h θ ( x ) = 1 1 + e − θ T X h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} X}} hθ(x)=1+e−θTX1带入到这样定义了的代价函数中时,我们得到的代价函数将是一个非凸函数
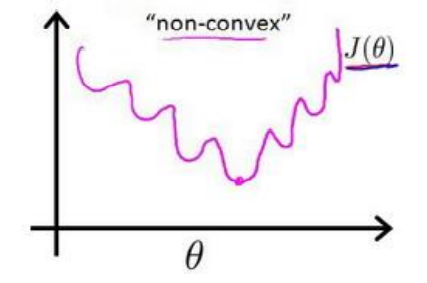
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
线性回归的代价函数为:
J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) J(θ)=m1∑i=1m21(hθ(x(i))−y(i))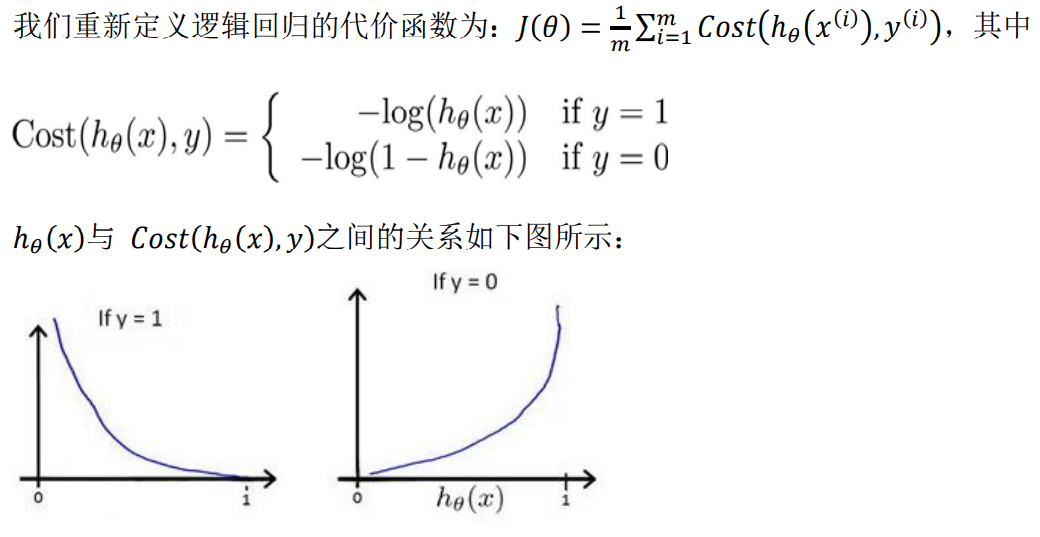

-
相关阅读:
性能测试指标之业务指标和技术指标如何进行区别
un8.1:在nacos微服务已经被注册user-center和content-center
自定义starter
怎样利用数据讲一个精彩故事?
Unity WebGL 编译 报错: emcc2: error: ‘*‘ failed: [WinError 2] ϵͳ�Ҳ���ָ�����ļ���解决办法
TypeScript 与组合式 API
C++之类与对象(2)
魔法的尽头是科技——用Python将普通视频变成动漫视频
国赛高教杯使用python/matlab必会基础数学建模-数据处理模块(课程4)
uniapp 对video视频组件嵌套倍速按钮
- 原文地址:https://blog.csdn.net/weixin_43845922/article/details/126554699