WGS84坐标系-地心地固坐标系-东北天坐标系

目录

1、前言

2、转换过程

3、代码示例

 4、参考资料

---

1、前言

工作中遇见个问题，就是ue4中，使用的坐标描述是使用东北天坐标系，因为如果经纬度只能表达到小数点后6位，这就造成有时间物体摆放位置不准确的问题。解决这个问题，就是把经纬度在转成ue里边能够使用的东北天坐标系。东北天坐标系又叫站心坐标系，这个站心可以是自己定义的。

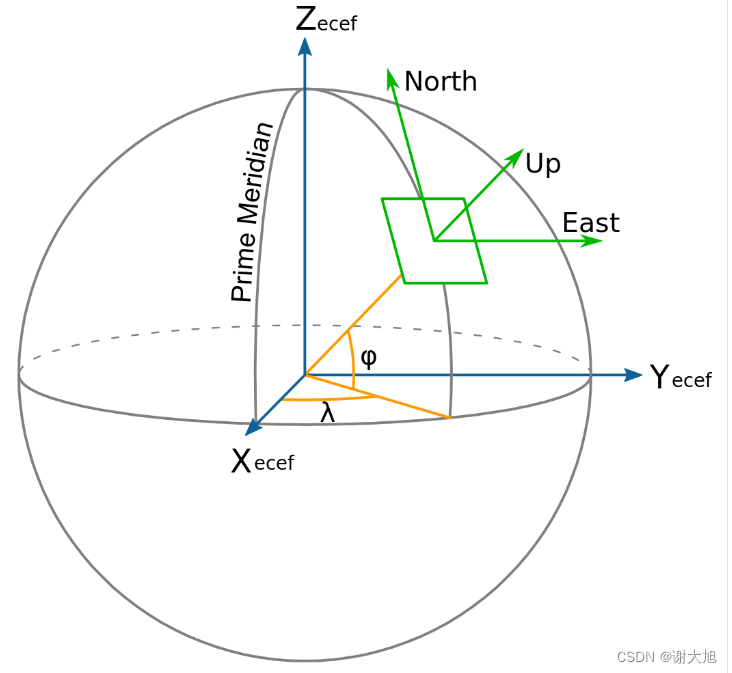
2、转换过程

本文标题：WGS84坐标系-地心地固坐标系-东北天坐标系

不熟悉地理坐标系的小伙伴可以看着比较晕，可以看下边：

• WGS84坐标系-地心地固坐标系

wgs84就是我们经常说的经纬度，那边经纬度只是我们讲地球划线，利用经纬度来确定地球上一个位置，但是当我们要计算地球上物体怎么进行位置变换或者距离计算时，我们需要把wgs84做坐标系转换，转换成适合计算的坐标系。因此，地心地固坐标系就是以笛卡尔坐标建立起来的坐标。并且这时候，地球是当作椭球来处理的。经纬度转笛卡尔坐标系可以看我之前这篇文章

(5条消息) 经纬度转笛卡尔坐标_谢大旭的博客-CSDN博客

• 地心地固坐标系-东北天坐标系

站心坐标系以一个站心点为坐标原点，当把坐标系定义为X轴指东、Y轴指北，Z轴指天，就是ENU（东北天）站心坐标系。这样，从地心地固坐标系转换成的站心坐标系，就会成为一个符合常人对地理位置认知的局部坐标系。同时，只要站心点位置选的合理（通常可选取地理表达区域的中心点），表达的地理坐标都会是很小的值，非常便于空间计算。

ENU、ECEF之间的转换，一个很明显的图形操作是平移变换，将站心移动到地心或者将地心转换到站心，另外一个需要进行的图形变换是旋转变换，其旋转变换矩阵根据P点所在的经度L和纬度B确定。但是的经纬度不适合计算旋转矩阵，旋转矩阵的计算应该在笛卡尔坐标系下来计算。

3、代码示例

#include <iostream>
#include <eigen3/Eigen/Eigen>
 
#include <osgEarth/GeoData>
 
using namespace std;
 
const double epsilon = 0.000000000000001;
const double pi = 3.14159265358979323846;
const double d2r = pi / 180;
const double r2d = 180 / pi;
 
const double a = 6378137.0;		//椭球长半轴
const double f_inverse = 298.257223563;			//扁率倒数
const double b = a - a / f_inverse;
//const double b = 6356752.314245;			//椭球短半轴
 
const double e = sqrt(a * a - b * b) / a;
 
void Blh2Xyz(double &x, double &y, double &z)
{
	double L = x * d2r;
	double B = y * d2r;
	double H = z;
 
	double N = a / sqrt(1 - e * e * sin(B) * sin(B));
	x = (N + H) * cos(B) * cos(L);
	y = (N + H) * cos(B) * sin(L);
	z = (N * (1 - e * e) + H) * sin(B);
}
 
void Xyz2Blh(double &x, double &y, double &z)
{
	double tmpX =  x;
	double temY = y ;
	double temZ = z;
 
	double curB = 0;
	double N = 0; 
	double calB = atan2(temZ, sqrt(tmpX * tmpX + temY * temY)); 
	
	int counter = 0;
	while (abs(curB - calB) * r2d > epsilon  && counter < 25)
	{
		curB = calB;
		N = a / sqrt(1 - e * e * sin(curB) * sin(curB));
		calB = atan2(temZ + N * e * e * sin(curB), sqrt(tmpX * tmpX + temY * temY));
		counter++;	
	} 	   
	
	x = atan2(temY, tmpX) * r2d;
	y = curB * r2d;
	z = temZ / sin(curB) - N * (1 - e * e);	
}
 
void TestBLH2XYZ()
{
	//double x = 113.6;
//double y = 38.8;
//double z = 100;	   
//   
//printf("原大地经纬度坐标：%.10lf	%.10lf	%.10lf
", x, y, z);
//Blh2Xyz(x, y, z);
 
//printf("地心地固直角坐标：%.10lf	%.10lf	%.10lf
", x, y, z);
//Xyz2Blh(x, y, z);
//printf("转回大地经纬度坐标：%.10lf	%.10lf	%.10lf
", x, y, z);
 
	double x = -2318400.6045575836;
	double y = 4562004.801366804;
	double z = 3794303.054150639;
 
	//116.9395751953      36.7399177551
 
	printf("地心地固直角坐标：%.10lf	%.10lf	%.10lf
", x, y, z);
	Xyz2Blh(x, y, z);
	printf("转回大地经纬度坐标：%.10lf	%.10lf	%.10lf
", x, y, z);
}
 
void CalEcef2Enu(Eigen::Vector3d& topocentricOrigin, Eigen::Matrix4d& resultMat)
{
	double rzAngle = -(topocentricOrigin.x() * d2r + pi / 2);
	Eigen::AngleAxisd rzAngleAxis(rzAngle, Eigen::Vector3d(0, 0, 1));
	Eigen::Matrix3d rZ = rzAngleAxis.matrix();
 
	double rxAngle = -(pi / 2 - topocentricOrigin.y() * d2r);
	Eigen::AngleAxisd rxAngleAxis(rxAngle, Eigen::Vector3d(1, 0, 0));
	Eigen::Matrix3d rX = rxAngleAxis.matrix();
 
	Eigen::Matrix4d rotation;
	rotation.setIdentity();
	rotation.block<3, 3>(0, 0) = (rX * rZ);
	//cout << rotation << endl;
				
	double tx = topocentricOrigin.x();
	double ty = topocentricOrigin.y();
	double tz = topocentricOrigin.z();
	Blh2Xyz(tx, ty, tz);
	Eigen::Matrix4d translation;
	translation.setIdentity();
	translation(0, 3) = -tx;
	translation(1, 3) = -ty;
	translation(2, 3) = -tz;
	
	resultMat = rotation * translation;
}
 
void CalEnu2Ecef(Eigen::Vector3d& topocentricOrigin, Eigen::Matrix4d& resultMat)
{
	double rzAngle = (topocentricOrigin.x() * d2r + pi / 2);
	Eigen::AngleAxisd rzAngleAxis(rzAngle, Eigen::Vector3d(0, 0, 1));
	Eigen::Matrix3d rZ = rzAngleAxis.matrix();
 
	double rxAngle = (pi / 2 - topocentricOrigin.y() * d2r);
	Eigen::AngleAxisd rxAngleAxis(rxAngle, Eigen::Vector3d(1, 0, 0));
	Eigen::Matrix3d rX = rxAngleAxis.matrix();
 
	Eigen::Matrix4d rotation;
	rotation.setIdentity();
	rotation.block<3, 3>(0, 0) = (rZ * rX);
	//cout << rotation << endl;
 
	double tx = topocentricOrigin.x();
	double ty = topocentricOrigin.y();
	double tz = topocentricOrigin.z();
	Blh2Xyz(tx, ty, tz);
	Eigen::Matrix4d translation;
	translation.setIdentity();
	translation(0, 3) = tx;
	translation(1, 3) = ty;
	translation(2, 3) = tz;
 
	resultMat = translation * rotation;
}
 
void TestXYZ2ENU()
{
	double L = 116.9395751953;
	double B = 36.7399177551;
	double H = 0;
	   	
	cout << fixed << endl;
	Eigen::Vector3d topocentricOrigin(L, B, H);
	Eigen::Matrix4d wolrd2localMatrix;
	CalEcef2Enu(topocentricOrigin, wolrd2localMatrix);	
	cout << "地心转站心矩阵：" << endl;
	cout << wolrd2localMatrix << endl<<endl;
 
	cout << "站心转地心矩阵：" << endl;
	Eigen::Matrix4d local2WolrdMatrix;
	CalEnu2Ecef(topocentricOrigin, local2WolrdMatrix);
	cout << local2WolrdMatrix << endl;
 
	double x = 117;
	double y = 37;
	double z = 10.3;
	Blh2Xyz(x, y, z);
 
	cout << "ECEF坐标（世界坐标）：";
	Eigen::Vector4d xyz(x, y, z, 1);
	cout << xyz << endl;
 
	cout << "ENU坐标（局部坐标）：";
	Eigen::Vector4d enu = wolrd2localMatrix * xyz;
	cout << enu << endl;	
}
 
void TestOE()
{
	double L = 116.9395751953;
	double B = 36.7399177551;
	double H = 0;
 
	osgEarth::SpatialReference *spatialReference = osgEarth::SpatialReference::create("epsg:4326");
	osgEarth::GeoPoint centerPoint(spatialReference, L, B, H);
 
	osg::Matrixd worldToLocal;
	centerPoint.createWorldToLocal(worldToLocal);
 
	cout << fixed << endl;
	cout << "地心转站心矩阵：" << endl;
	for (int i = 0; i < 4; i++)
	{
		for (int j = 0; j < 4; j++)
		{
			printf("%lf	", worldToLocal.ptr()[j * 4 + i]);
		}
		cout << endl;
	}
	cout << endl;
 
	osg::Matrixd localToWorld;
	centerPoint.createLocalToWorld(localToWorld);
 
	cout << "站心转地心矩阵：" << endl;
	for (int i = 0; i < 4; i++)
	{
		for (int j = 0; j < 4; j++)
		{
			printf("%lf	", localToWorld.ptr()[j * 4 + i]);
		}
		cout << endl;
	}
	cout << endl;
 
	double x = 117;
	double y = 37;
	double z = 10.3;
	osgEarth::GeoPoint geoPoint(spatialReference, x, y, z);
 
	cout << "ECEF坐标（世界坐标）：";
	osg::Vec3d out_world;
	geoPoint.toWorld(out_world);
	cout << out_world.x() <<'	'<< out_world.y() << '	' << out_world.z() << endl;
	   
	cout << "ENU坐标（局部坐标）：";
	osg::Vec3d localCoord = worldToLocal.preMult(out_world);
	cout << localCoord.x() << '	' << localCoord.y() << '	' << localCoord.z() << endl;
}
 
int main()
{
	//TestBLH2XYZ();
 
	cout << "使用Eigen进行转换实现：" << endl;
	TestXYZ2ENU();
 
	cout <<"---------------------------------------"<< endl;
	cout << "通过OsgEarth进行验证：" << endl;
	TestOE();
}

 4、参考资料

本着深入学习的态度，经过一番搜索，又找到一篇博客。直接带我起飞。

地心地固坐标系(ECEF)与站心坐标系(ENU)的转换 - 走看看 (zoukankan.com)