-
(二十四)数据结构-选择排序
选择排序(每一趟在待排序元素中选择关键字最小(或最大)的元素加入有序子序列)分为:
- 简单选择排序
- 堆排序
1.1简单选择排序算法思想
每一趟中在待排元素中选取关键字最小的元素加入有子序列
举例说明:
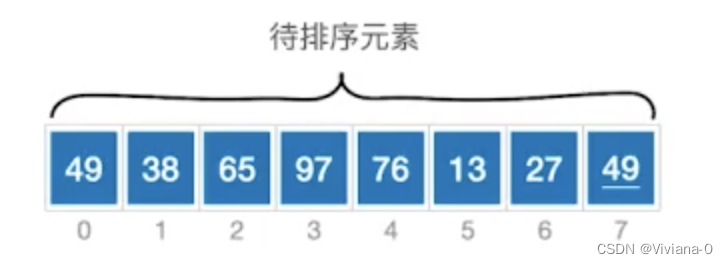
- 第一趟从待排序列中,左往右依次找到最小元素(13),接着与起始元素(49)进行交换,得到13 38 65 97 76 49 27 49
- 第一趟从待排序列中(38 65 97 76 49 27 49)从左往右依次找到最小元素(27),接着与待排序列起始元素(38)进行交换,得到13 27 38 65 97 76 49 38 49
- 依次列推
- 当出现两个49,则将最靠近的进行交换
- 当出现剩一个元素则不再处理
1.2算法性能分析
算法的时间复杂度不会因为给出的序列而改变,n个元素就需要n-1趟处理
算法是不稳定的
适用性:顺序表、链表
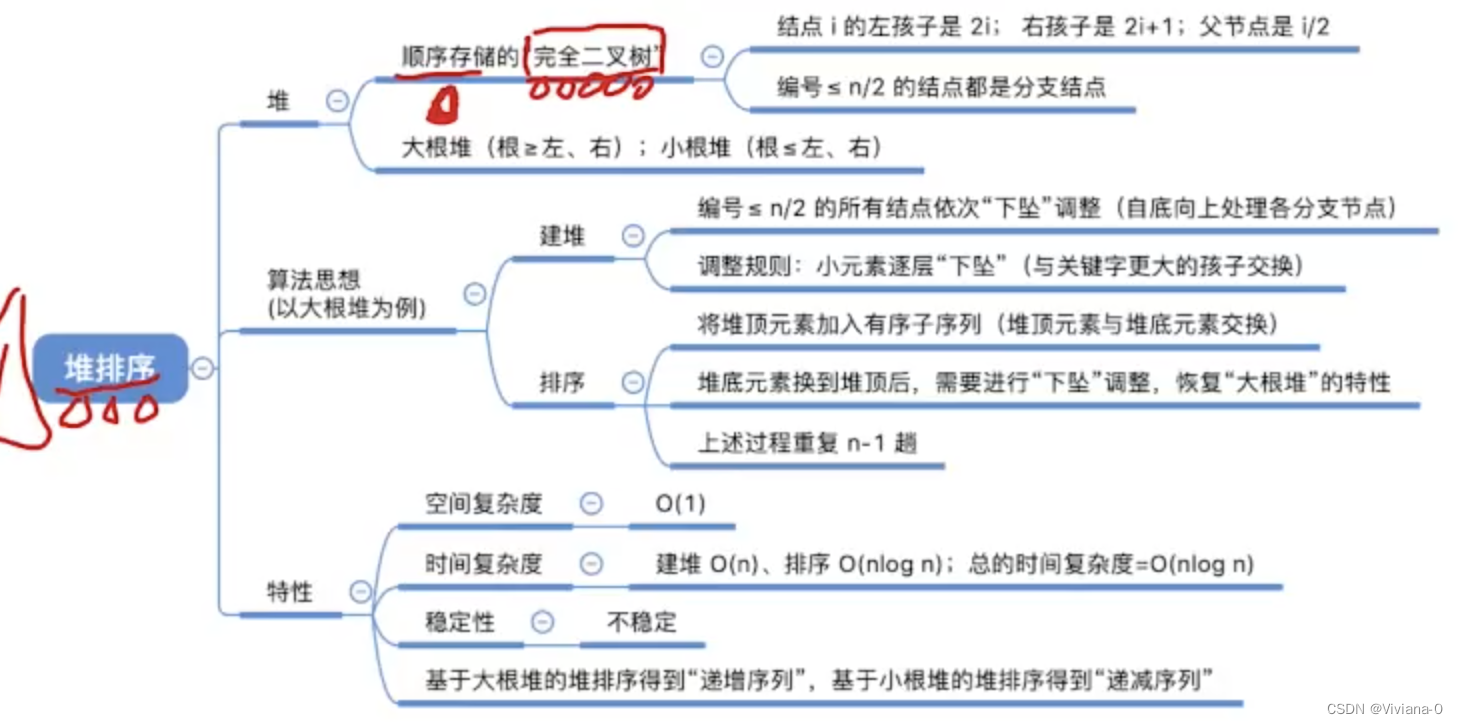
二、堆排序(重要)
2.1.1“堆”的概念

大根堆:在完全二叉树中,根>= 左、右(堆顶元素关键字最大)
小根堆:在完全二叉树中,根<= 左、右

2.1.2建立大根堆
思路:把所有
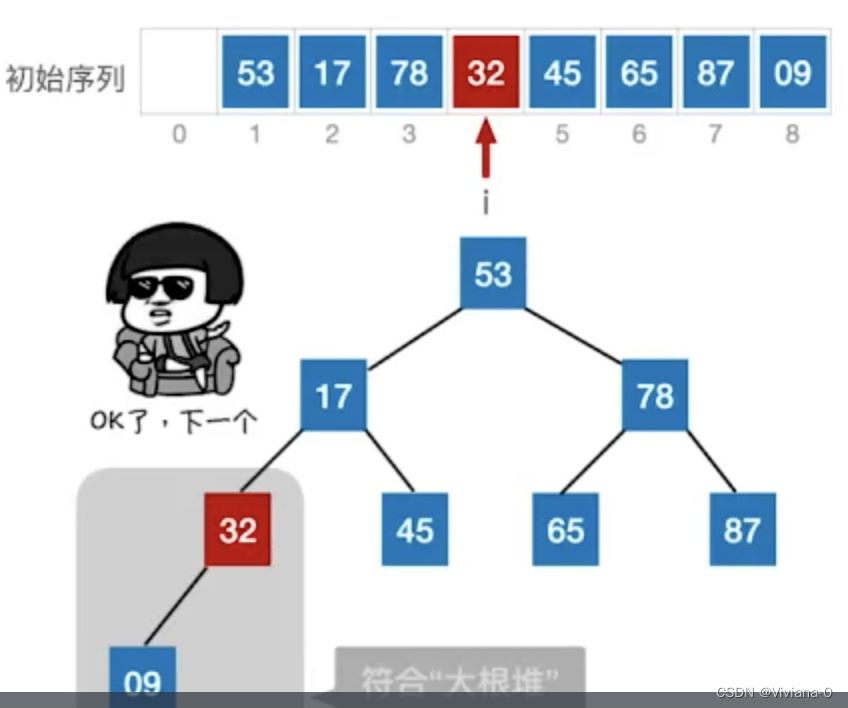
非终端结点(i<=[n/2])都检查一遍,是否满足大根堆的要求,如果不满足,则进行调整- 非中断结点=8/2=4,我们处理i<=4的结点,从后往前进行处理,处理编号结点中最大的。
- 第一个处理的结点为4号结点(值为9),检查9是否满足大根堆的要求
- 发现他只有左孩子,且左孩子的值比她更大,因此不满足大根堆特性
- 因此将当前结点(9)与更大的一个孩子(32)进行互换


-
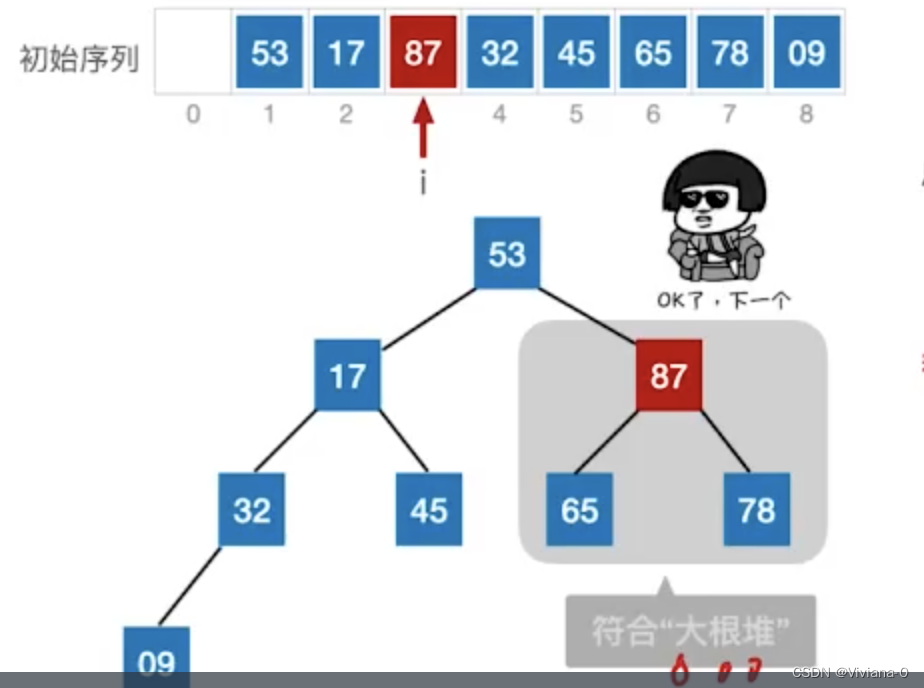
处理结点编号为3的结点(78),将当前结点78与更大的一个孩子(87)结点进行交换
-
处理结点编号为2的结点(17),若有两个孩子结点都比当前结点的值更大,那么将当前结点17与最大的一个孩子(45)结点进行交换
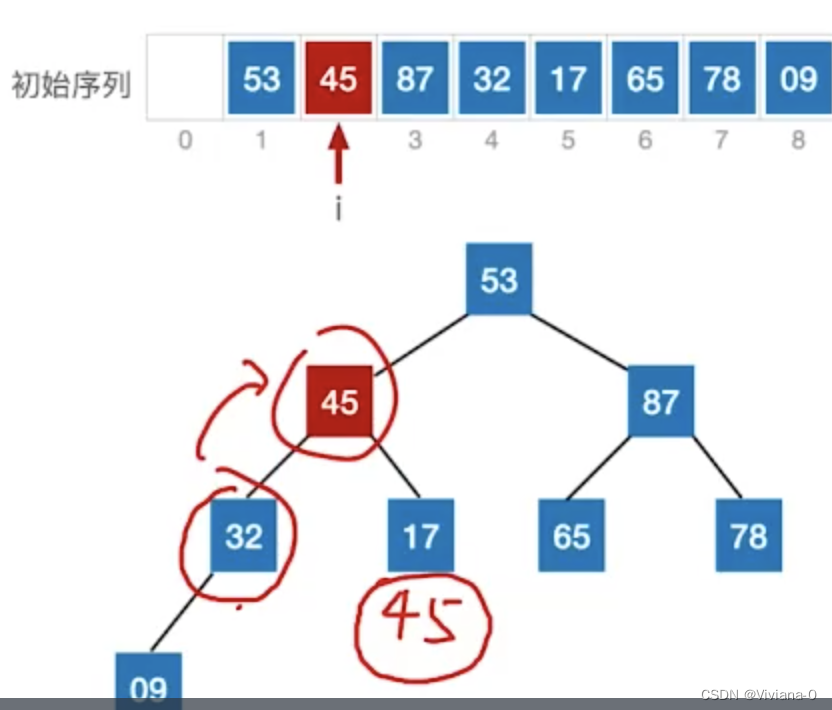
-
处理结点编号为1的结点(53)时,会让87替换53,但是会使得53出现“下坠”,可能会导致下一层的子树不符合大根丢的要求,则需要在继续进行往下调整,当无法继续下坠,即调整完整

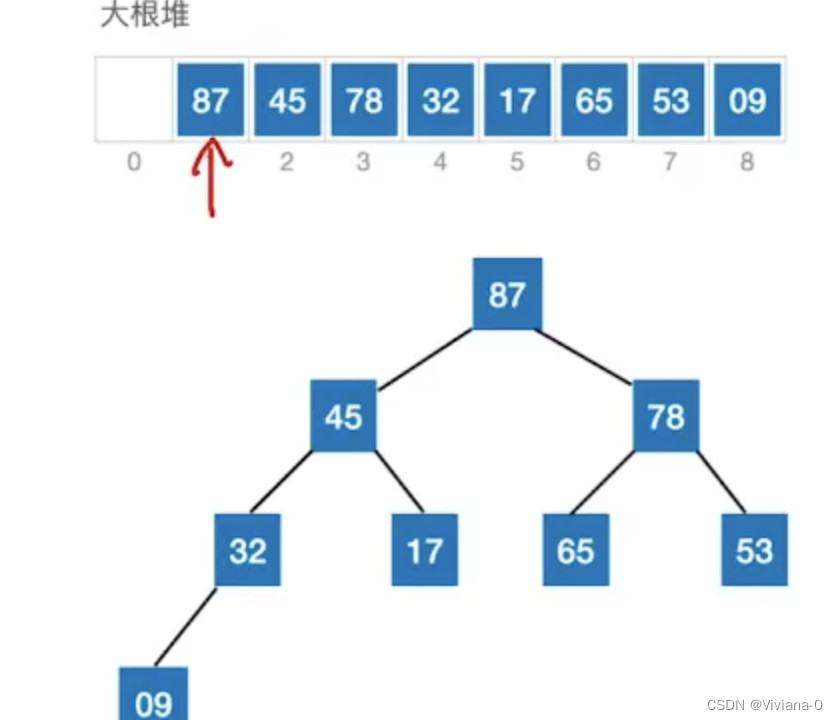
2.1.3基于大根堆进行排序
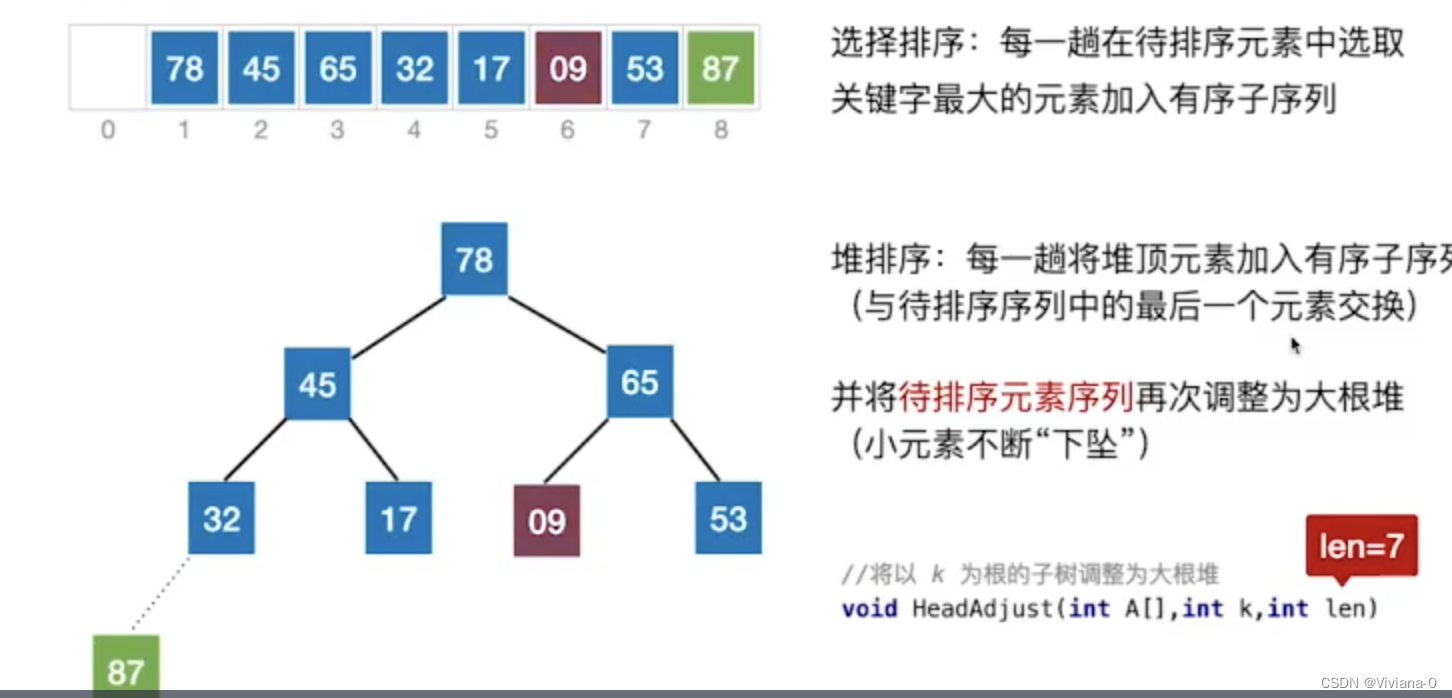
思想:每一趟将堆顶元素加入到有序子序列(与待排序列中的最后一个元素交换),将待排序元素序列再次调整为大根堆
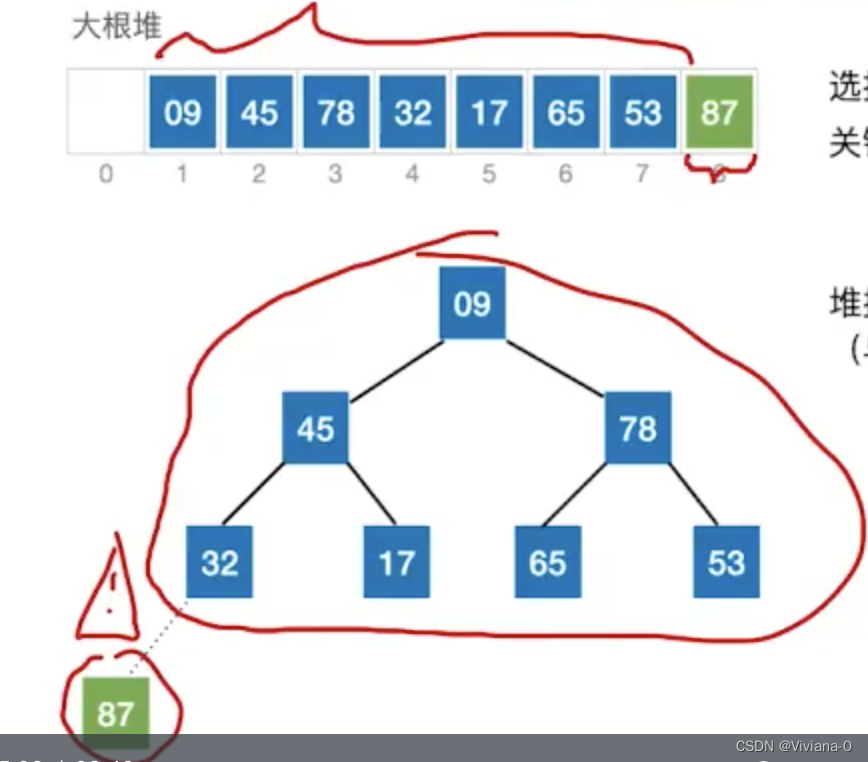
- 首先堆顶元素(87)换到末尾,09元素换到堆顶,后面87这个元素将不再改变,接着将除87以外的元素看成一个堆
- 当我们把09元素换到堆顶,接下来我们要对09元素进行“下坠”调整
- 依次列推
- 直到只剩下最后一个待排元素,则不再调整
2.2算法效率分析
若左右孩子一样大,我们将左孩子进行交换
堆排序是不稳定的

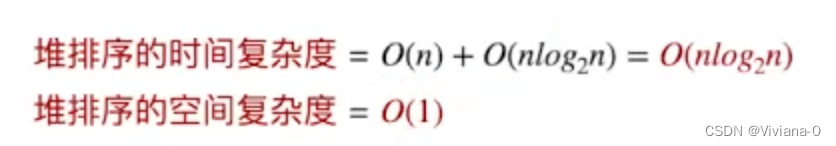
2.3知识点回顾
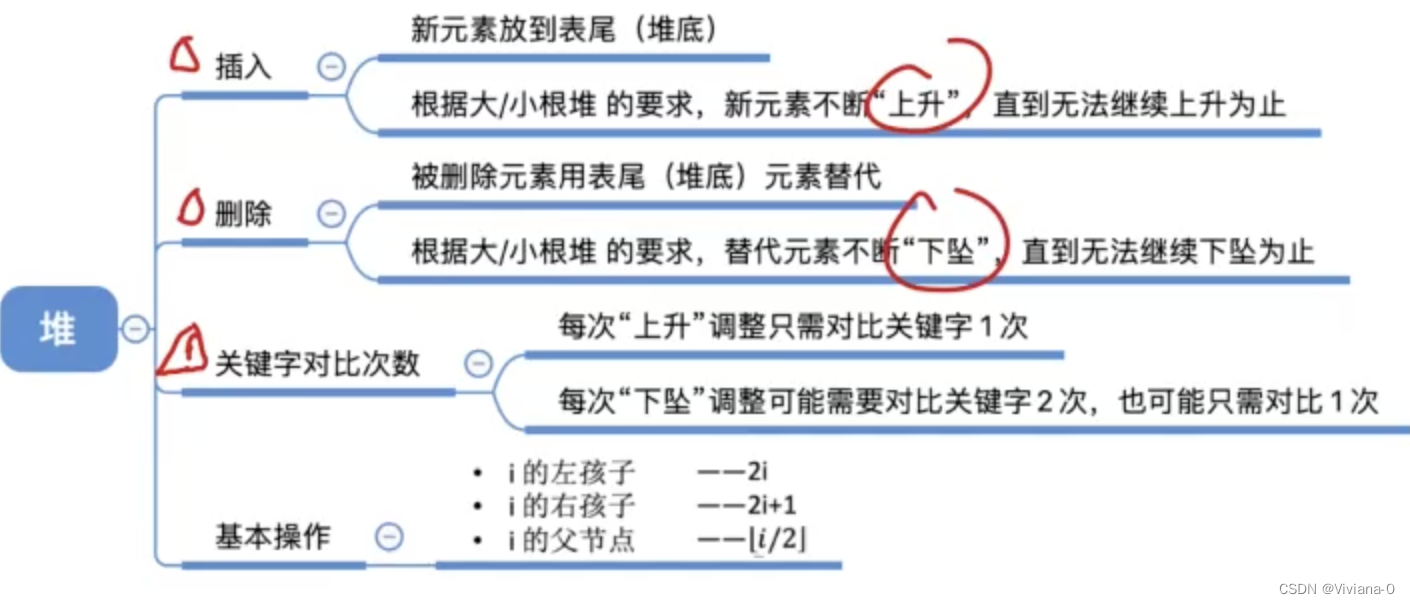
2.4堆排序的插入删除
关键字对比次数:
- “上升”调整只需对比关键字一次
- “下降”调整需要对比关键字两次,也可能只需对比1次
-
相关阅读:
SpringBoot:容器中添加视图解析器
城市机会清单中处处是机遇——实现pdf转excel
【已解决】vue后台页面跳转无法正常显示
java的file类的常用的操作实战分享来啦
小猴吃苹果-第12届蓝桥杯Scratch选拔赛真题精选
zabbix6.0 部署配置
javaEE幼儿园学生管理系统
计算机网络 第一章 计算机网络体系结构
TDengine 社区问题双周精选 | 第三期
Fiddler抓取的一些问题
- 原文地址:https://blog.csdn.net/weixin_45579930/article/details/126557884