经纬度转笛卡尔坐标

目录

前言

二、默认地球的正球

1、经纬度转笛卡尔坐标

 2、笛卡尔坐标系转经纬度

三、默认地球是椭球

        1、 BLH->XYZ

2、XYZ->BLH

3、总结

---

前言

工作过程经常遇见需要把经纬度转成笛卡尔坐标系来描述空间物体，但是所谓的笛卡尔坐标，其实看起来就是具备XYZ值的坐标，那么怎么计算？这要将地球看正球还是椭球，不同定义，算法不一样，得到的结果也不一样。

二、默认地球的正球

1、经纬度转笛卡尔坐标

public static double EarthRadius = 6371; // km

 public static Point3D LatLonToPoint(double latitude, double longitude)
        {
            longitude -= 180;
            latitude = latitude / 180 * Math.PI;
            longitude = longitude / 180 * Math.PI;
            return new Point3D(
                EarthRadius * Math.Cos(latitude) * Math.Cos(longitude),
                EarthRadius * Math.Cos(latitude) * Math.Sin(longitude),
                EarthRadius * Math.Sin(latitude));
        }

 2、笛卡尔坐标系转经纬度

public static void PointToLatLon(Point3D pt, out double lat, out double lon)
        {
            lon = Math.Atan2(pt.Y, pt.X) * 180 / Math.PI;
            lon += 180;
            if (lon > 180) lon -= 360;
            if (lon < -180) lon += 360;
            double a = Math.Sqrt(pt.X * pt.X + pt.Y * pt.Y);
            lat = Math.Atan2(pt.Z, a) * 180 / Math.PI;
        }

三、默认地球是椭球

一般默认球是椭球时候，使用的坐标系定义是地心地固坐标系。这个坐标系以椭球球心为原点，本初子午面与赤道交线为X轴，赤道面上与X轴正交方向为Y轴，椭球的旋转轴(南北极直线)为Z轴。显然，这是个右手坐标系：

1、 BLH->XYZ

将P点所在的子午椭圆放在平面上，以圆心为坐标原点，建立平面直接坐标系：

 

 那么，关键问题在于求子午面直角坐标系的x,y。过P点作原椭球的法线Pn，他与子午面直角坐标系X轴的夹角为B；过P点作子午椭圆的切线，它与X轴的夹角为(90°+B):

 

 

 通过式（5）式（6），可以计算椭球上某一点的坐标。但这个点并不是我们真正要求的点，我们要求的点P(B,L,H)是椭球面沿法向量向上H高度的点：

矢量在任意位置的方向都是一样的，那么我们可以假设存在一个单位球(球的半径为单位1)，将法线单位矢量移动到球心位置，可得法线单位矢量为：

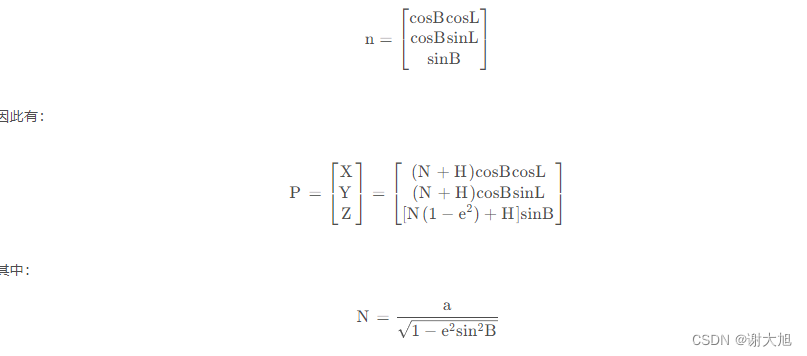
2、XYZ->BLH

 

 3、总结

转换公式总结

 实现代码：

#include <iostream>
 
using namespace std;
 
const double epsilon = 0.000000000000001;
const double pi = 3.14159265358979323846;
const double d2r = pi / 180;
const double r2d = 180 / pi;
 
const double a = 6378137.0;		//椭球长半轴
const double f_inverse = 298.257223563;			//扁率倒数
const double b = a - a / f_inverse;
//const double b = 6356752.314245;			//椭球短半轴
 
const double e = sqrt(a * a - b * b) / a;
 
void Blh2Xyz(double &x, double &y, double &z)
{
	double L = x * d2r;
	double B = y * d2r;
	double H = z;
 
	double N = a / sqrt(1 - e * e * sin(B) * sin(B));
	x = (N + H) * cos(B) * cos(L);
	y = (N + H) * cos(B) * sin(L);
	z = (N * (1 - e * e) + H) * sin(B);
}
 
void Xyz2Blh(double &x, double &y, double &z)
{
	double tmpX =  x;
	double temY = y ;
	double temZ = z;
 
	double curB = 0;
	double N = 0; 
	double calB = atan2(temZ, sqrt(tmpX * tmpX + temY * temY)); 
	
	int counter = 0;
	while (abs(curB - calB) * r2d > epsilon  && counter < 25)
	{
		curB = calB;
		N = a / sqrt(1 - e * e * sin(curB) * sin(curB));
		calB = atan2(temZ + N * e * e * sin(curB), sqrt(tmpX * tmpX + temY * temY));
		counter++;	
	} 	   
	
	x = atan2(temY, tmpX) * r2d;
	y = curB * r2d;
	z = temZ / sin(curB) - N * (1 - e * e);	
}
 
int main()
{
	double x = 113.6;
	double y = 38.8;
	double z = 100;	   
	   
	printf("原大地经纬度坐标：%.10lf\t%.10lf\t%.10lf\n", x, y, z);
	Blh2Xyz(x, y, z);
 
	printf("地心地固直角坐标：%.10lf\t%.10lf\t%.10lf\n", x, y, z);
	Xyz2Blh(x, y, z);
	printf("转回大地经纬度坐标：%.10lf\t%.10lf\t%.10lf\n", x, y, z);	 
}

参考资料：

(5条消息) 大地经纬度坐标与地心地固坐标的的转换_charlee44的博客-CSDN博客_地心坐标系转换为经纬坐标