王道数据结构5.2（树的应用）

一、二叉排序树

(一) 基础

1. 定义：又称为二叉查找树，一棵二叉树或空二叉树，或者具有如下性质的二叉树：
   ① 左子树上所有结点的关键字均小于根结点的关键字。
   ② 右子树上所有结点的关键字均大于根结点的关键字。
   ③ 左右子树又各是一棵二叉排序树。
2. 利用中序遍历，可以得到一个递增的有序序列。

(二) 操作

1. 二叉排序树的查找

（1）思想：
若树非空，目标值与根结点的值比较：
①若相等，则查找成功。
②若小于根结点，则查找左子树，若大于根结点，则查找右子树
查找成功则返回节点指针，查找失败，则返回NULL。
（2）代码：

//二叉排序树结点 
typedef struct BSTNode{
    int key;
    struct BSTNode *lchild,*rchild;
}BSTNode,*BSTree;
//在二叉排序树中查找值为key的结点（非递归）
BSTNode *BST_Search(BSTNode T,int key){
   while(T!=NULL&&key!=T->key){
        if(key<T->key)
           T=T->lchild;
        else T=T->rchild;
   }
   return T;
}
//在二叉排序树中查找值为key的结点（递归）
BSTNode *BSTSearch(BSTree T,int key){
    if(T==NULL)
        returm NULL;
    if(key==T->key)
        return T;
    else if(key==T->key)
        return BSTSearch(T->lchild,key)；
    else
        return BSTSearch(T->rchild,key);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

3. 分析：
   ① 非递归算法时间复杂度为O(1)
   ② 最坏时间复杂度为O(h)

2. 二叉排序树的插入

1. 思想：若原二叉排序树为空，则直接插入结点，否则，若关键字k小于根结点值，则插入左子树，若关键字k大于根结点，则插入到右子树。
2. 代码：

//在二叉排序树插入关键字k的新结点（递归实现）
int BST_Insert(BSTree &T,int k){
  if(T==NULL){
     T=(BSTree)malloc(sizeof(BSTNode));
    T->key=k;
    T->lchild=T->rchild=NULL;
    return 1;
  }
  else if(k==T->key)
    return 0;
  else if(k<T->key)
    return BST_Insert(T->lchild,k);
  else 
    return BST_Insert(T->rchild,k);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

3. 二叉排序树的构造

1. 代码：

//按照str[]中的关键字序列建立二叉排序树
void Creat_BST(BSTree &T,int str[],int n){
  T=NULL;
  int i=0;
  while(i<n){
    BST_Insert(T,str[i]);
    i++;
  }
}
//插入结点
int BST_Insert(BSTree &T,int k){
  if(T==NULL){
     T=(BSTree)malloc(sizeof(BSTNode));
    T->key=k;
    T->lchild=T->rchild=NULL;
    return 1;
  }
  else if(k==T->key)
    return 0;
  else if(k<T->key)
    return BST_Insert(T->lchild,k);
  else 
    return BST_Insert(T->rchild,k);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

2. 分析：
   不同的str[]序列可能得到同款二叉排序树，也可能得到不同的二叉排序树。
3. 实例
   

4. 二叉排序树的删除

1. 思想：
   （1） 先搜索找到目标节点：
   ① 如果被删除节点是叶子结点，则直接删除，不会破坏二叉排序树的性质
   ② 若z结点只有一棵左子树或右子树，则让z的子树成为z父节点的子树，代替z的位置。
   ③ 若z结点存在左右子树，则令z的直接后继（或直接前驱）代替z，然后从二叉排序树中山区这个直接后继（或直接前驱），这样就转换成了①或②情况。【z的后继：z的右子树中最左下结点，该结点一定没有左子树；z的前驱：z的左子树中最右下结点，该结点一定没有右子树】
   

5. 查找效率分析

1. 查找长度—在查找算法中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度。
2. 若树高h，为了找到最下层的结点需要对比h次。
3. 最好情况：n个结点的二叉树最小高度为log2n+1【向下取整】
4. 最坏情况：每个结点只有一个分支，树高h=节点数n，平均查找长度=O(n)
5. 实例
   ① 查找成功的平均查找时间
   
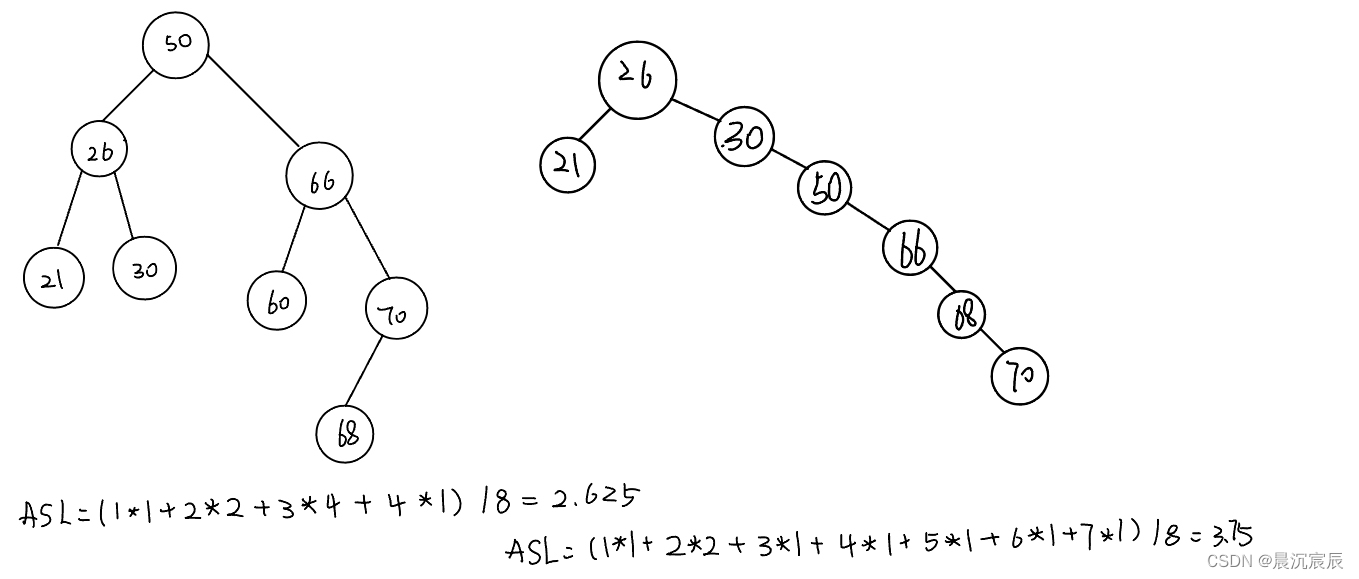
   查找失败的平均查找长度ASL
   

二、平衡二叉树

（一）定义

1. 简称平衡树（AVL树）—书上任意结点的左子树和右子树的高度之差不超过1。【G.M.Adelson-Velsky和E.M.Landis】
2. 结点的平衡因子=左子树高-右子树高。
3. 平衡二叉树结点的平衡因子的值只可能是-1,0或1。只要有任意一点平衡因子绝对值大于1，则不是平衡二叉树。
4. 构造结构

//二叉排序树结点 
typedef struct AVLNode{
    int key;
    int balance;//平衡因子
    struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;
1
2
3
4
5
6

（二）操作

1. 二叉平衡树的插入

（1）最小不平衡子树：从插入点往回找到第一个不平衡节点，调整以该结点的根的子树。
（2）插入后查找路径上的所有结点的平衡因子都会发生变化。
（3）寻找最小不平衡子树

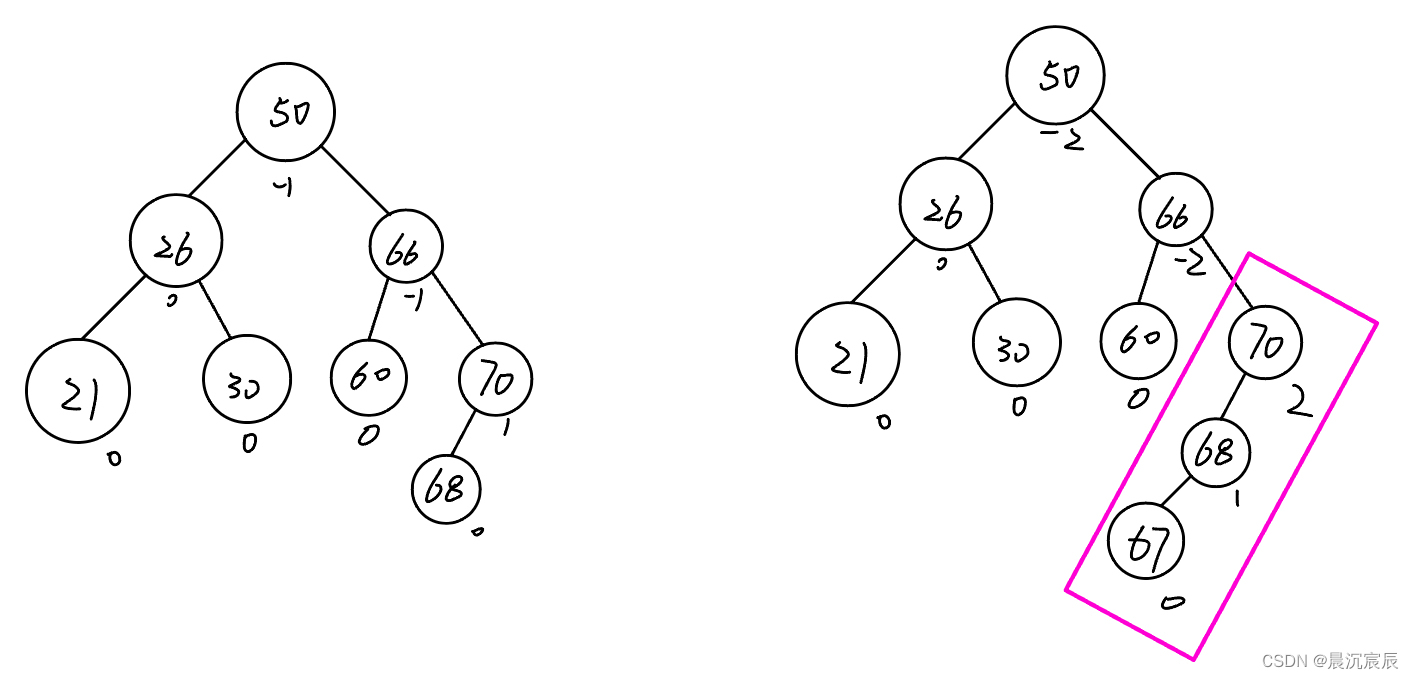
（4）只需要将最小不平衡子树调整平衡，其他祖先结点都会恢复平衡。
（5）调整不平衡子树
① LL（在A的左孩子的左子树中插入导致不平衡）
右单旋转：由于在结点A的左孩子的左子树上插入了新结点，A的平衡因子从1增至2，导致以A上为根的子树失去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树。

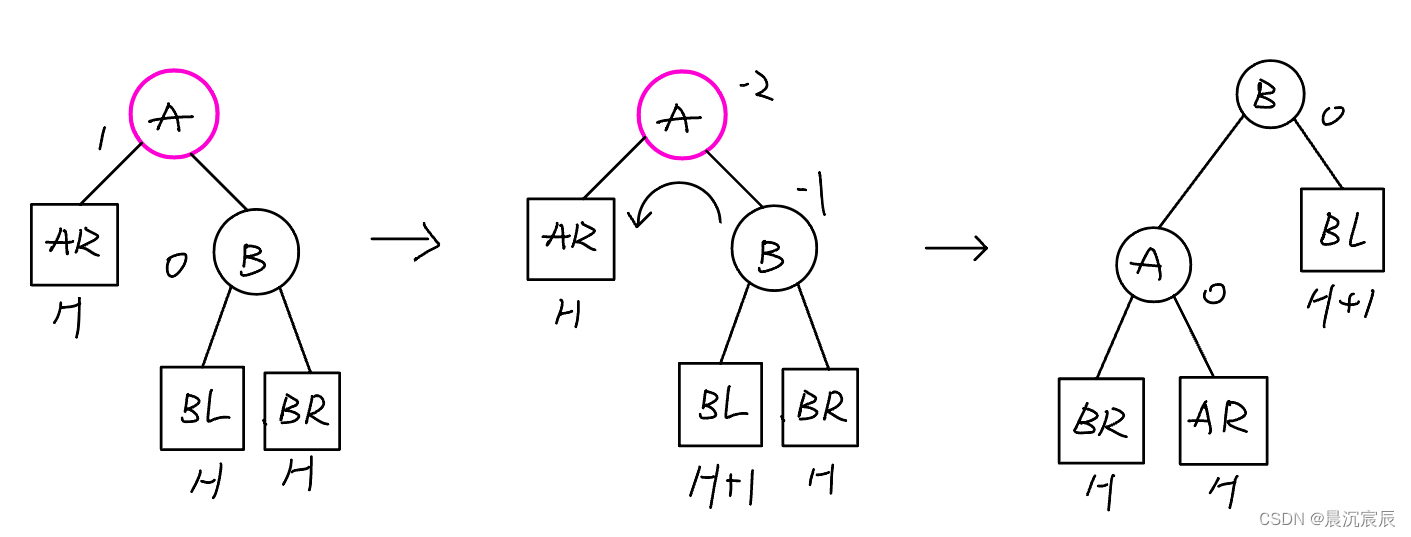
②RR（在A的右孩子的右子树中插入导致不平衡）
左单旋转：由于在结点A的右孩子的右子树上插入了新结点，A的平衡因子从-1增至-2，导致以A上为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树。

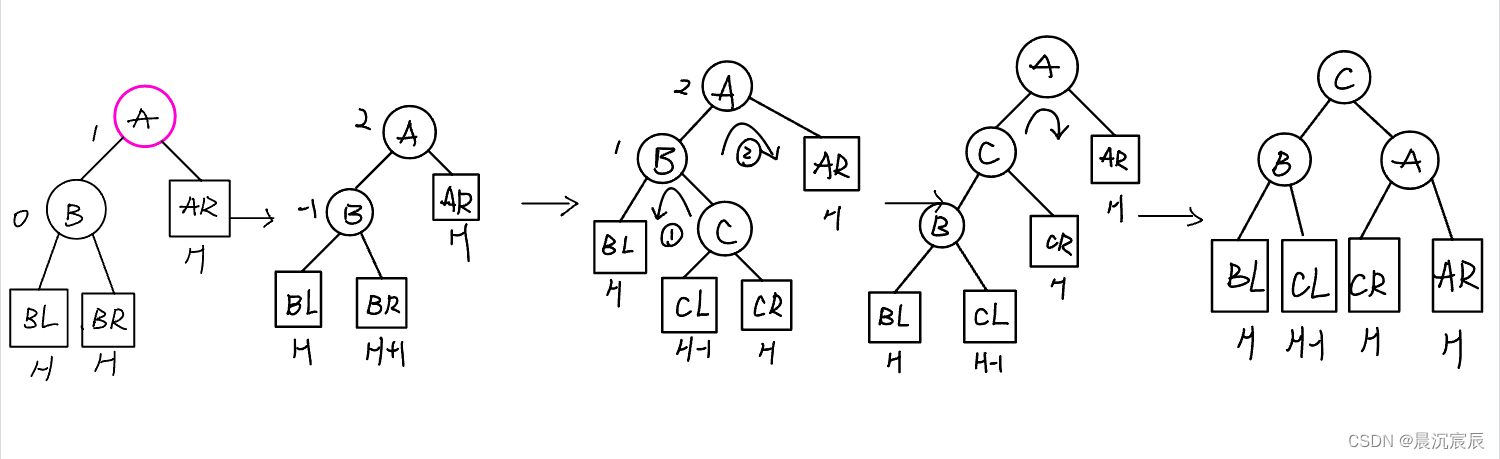
③ LR（在A的左孩子的右子树中插入导致不平衡）
先左旋后右旋：由于在A的左孩子L的右子树R上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋后右旋。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置。

④ RL（在A的右孩子的左子树中插入导致不平衡）
先右后左旋转
由于在A的右孩子L的左子树R上插入新结点，A的平衡因子由-1增至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋后左旋。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置。
（6）代码

• 实现f向右下旋转，p向右上旋转：其中f是父节点，p为左孩子，gf为f的父节点

  f->lchild=p->rchild;
    p->rchild=f;
    gf->lchild/rchild = p;
1
2
3

• 实现f向左下旋转，p向左上旋转：其中f是父节点，p为右孩子，gf为f的父节点

  f->rchild=p->lchild;
    p->lchild=f;
    gf->lchild/rchild = p;
1
2
3

2. 查找效率分析
   （1）若树高为h，则最坏情况下，查找一个关键字最多需要对比h次，即查找操作的时间复杂度不可能超过O(h)。
   （2）平衡二叉树——树上任意结点的左子树和右子树的高度之差不超过1。
   （3）假设以nh表示深度为h的平衡树中含有最少节点数。则有n0=0，n1=1，n2=2，并且有nh=nh-1+nh-2+1。【n3=4，n4=7，n5=12，n=9，则说明高最大为4】
   可以证明含有n个结点的平衡二叉树的最大深度为O(log2n)，平衡二叉树的平均查找长度为O(log2n)。

三、哈夫曼树

1. 带权路径长度

（1）结点的权：有某种现实含有的数值（如：表示结点的重要性等）
（2）结点的带权路径长度：从树的根到该结点的路径长度（经过的边数）与该结点上权值的乘积。
（3）树的带权路径长度：树中所有叶结点的带权路径长度之和wpl
（4）在含有n个带权也结点的二叉树中，其中带权路径长度最小的二叉树称为哈夫曼树，也称最优二叉树。

2.哈夫曼树的构造

（1）给定n个权值分别为w1, w2,…, wn的结点，构造哈夫曼树的算法描述如下：
1）将这n个结点分别作为n棵仅含一个结点的二叉树，构成森林F。
2）构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新
结点的权值置为左、右子树上根结点的权值之和。
3）从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
4）重复步骤2）和3），直至F中只剩下一棵树为止。

（2）规律：

• 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大
• 哈夫曼树的结点总数为2n − 1
• 哈夫曼树中不存在度为1的结点。
• 哈夫曼树并不唯一，但WPL必然相同且为最优

3. 哈夫曼编码

100个选择题的答案
（1）固定长度编码——每个字符用相等长度的二进制位表

• ASCII编码
  A——0100 0001
  B——0100 0010
  C——0100 0011
  D——0100 0100
  8*100=800
• 每个字符用长度为2的二进制表示
  假设，100题中有80题选C，10题选A，8题选B，2题选D
  所有答案的二进制长度=802+102+82+22=200 bit
  （2）可变长度编码——允许对不同字符用不等长的二进制位表示
  若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码
  
  （3）有哈夫曼树得到哈夫曼编码——字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点的权值，根据之前介绍的方法构造哈夫曼树.
  （4）注意：
  ① 哈夫曼树不唯一，因此哈夫曼编码不唯一。
  ② 哈夫曼编码可用于数据压缩。