寒假训练——第三周（状压DP）

A - 入门-状压递推

A - 入门-状压递推

思路：

• 状压 $DP$ + 递推

具体实现：

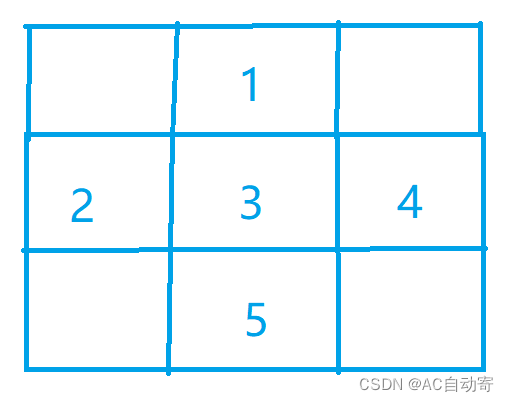
• b[i][j]可与b[i-2][j] 和 b[i-1][j-1] 和 b[i-1][j+1]共同决定
• 因为b[i][j]为四周为偶数，若其他三边一直，则b[i][j]这最后一边就可以推出来，相等于已知
• 例如
• 5 可以有 1 2 4 共同推出
  
• 然后，我们用O(2^n)枚举第一行的所有状态，如此判断是否满足情况
• 总时间复杂度为：$O(n\ast n\ast 2^n)$ 约等于 $7\ast 1e6$ 可以过去

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define mkpr make_pair
#define x first
#define y second
//#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 30, M = 5;
const int YB = 8, YM = 1e8;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

int a[N][N], b[N][N];

int check(int s)
{
    memset(b, 0, sizeof b);
    
    for (int i = 0; i < n; i ++ )
    {
        if((s >> i) & 1) b[0][i] = 1;
        else if(a[0][i]) return INF;
    }
    
    for (int i = 1; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
        {
            int sum = 0;
            if(i > 1) sum += b[i - 2][j];
            if(j > 0) sum += b[i - 1][j - 1];
            if(j < n - 1) sum += b[i - 1][j + 1];
            
            b[i][j] = sum & 1;
            
            if(!b[i][j] && a[i][j]) return INF;
        }
    
    int res = 0;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            if(a[i][j] ^ b[i][j]) res ++;
    
    return res;
}

void solve()
{
    cin >> n;
    
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            scanf("%d", &a[i][j]);
    
    int res = INF;
    for (int i = 0; i < 1 << n; i ++ )
        res = min(res, check(i));
    
    printf("Case %d: ", cases);
    if(res == INF) printf("-1\n");
    else printf("%d\n", res);

    return;
}

signed main()
{
    //fast;
    T = 1;
    scanf("%d", &T);
    
    // while(T -- )
    for (cases = 1; cases <= T; cases ++ )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

B - 入门-状压dfs

B - 入门-状压dfs

思路：

• 暴力 $DFS$ 放即可，
• 化二维数组为一维的二进制数，格子数位置与二进制的位数是唯一（最多16位）
• s >> i & 1判断i位置是否过方块，s | 1 << i表示在i位置放上方块，连续|表示连续放方块

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define mkpr make_pair
#define x first
#define y second
//#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 30, M = 5;
const int YB = 8, YM = 1e8;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

int H, W, A, B;
int ans;

void dfs(int s, int bit, int a, int b)
{
    if(s == H * W)
    {
        ans ++;
        return;
    }
    
    // 此处已经填过了，直接到下一个格子
    if( bit >> s & 1) return dfs(s + 1, bit, a, b);
    
    // 先填 1x2 的格子，因为有分支，可以递归到所有更多情况
    if(a)
    {
        // 横着放
        if(s % W < W - 1 && !(bit >> s + 1 & 1) ) dfs(s + 1, bit | 1 << s | 1 << s + 1, a - 1, b);
        // 竖着放
        if(s + W < H * W) dfs(s + 1, bit | 1 << s | 1 << s + W, a - 1, b);
    }
    
    // 填 1x1 的格子
    if(b) return dfs(s + 1, bit | 1 << s, a, b - 1);
    
    return;
}

void solve()
{
    cin >> H >> W >> A >> B;
    
    dfs(0, 0, A, B);
    
    cout << ans << endl;
    
    return;
}

signed main()
{
    T = 1;
    //fast;cin >> T;
    //scanf("%d", &T);
    
    //for (cases = 1; cases <= T; cases ++ )
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

---

C - 经典状压DP

C - 经典状压DP

思路：

• 预处理状压状态，判断状态合理

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define mkpr make_pair
#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 13, M = 5;
const int YB = 8, YM = 1e8;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

int row[N], st[1 << N];
int f[1 << N][1 << N];

void solve()
{
    cin >> n >> m;
    
    // 输入每一行的二进制表示状态
    for (int i = 1; i <= n; i ++ )  
        for (int j = 0; j < m; j ++ )
        {
            int x;
            cin >> x;
            row[i] |= x << j;
        }
    
    // 预处理不含相邻 1 的状态
    int idx = 0;
    for (int i = 0; i < 1 << m; i ++ )
        if( !(i & i << 1) )
            st[idx ++ ] = i;
    
    // 预处理满足第一行的状态
    for (int i = 0; i < idx; i ++ )
        if( (row[1] & st[i]) == st[i])
            f[1][i] = 1;
    
    // 递推计算其他行的状态
    for (int i = 2; i <= n; i ++ )
        for (int j = 0; j < idx; j ++ )
            if( (row[i] & st[j]) == st[j])
                for (int k = 0; k < idx; k ++ )
                    if( !(st[j] & st[k]) )
                        f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
    
    // 计算第 n 行的合理方案
    int res = 0;
    for (int i = 0; i < idx; i ++ )
        res = (res + f[n][i]) % mod;
    
    cout << res << endl;
    
    return;
}

signed main()
{
    T = 1;
    //fast;cin >> T;
    //scanf("%d", &T);
    
    //for (cases = 1; cases <= T; cases ++ )
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

---

D - 鸽巢原理+状压枚举

D - 鸽巢原理+状压枚举

思路：

• 抽屉原理 + 状压枚举（貌似和题目重复了，，问题不大）

具体实现：

• 问题为：找到 和 mod 200的两组数据
• 我们可知2^8-1 = 255, 255 > 200所以我们至多只需枚举前8位数的所有方案即可枚举出答案
• 因为即使每一种方案都尽量不同，但总方案为255至少会有55个重复答案的，这就是著名的抽屉原理（鸽巢原理）的简化思路，如此我们利用二进制枚举即可完美解决此问题

总结一下：

• 思路清晰！
• 代码简介！

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define mkpr make_pair
#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 200;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 210, M = 5;
const int YB = 8, YM = 1e8;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

int a[N];
vector<vector<int>> g[N];

void print(int x)
{
    int t1 = g[x][0].size(), t2 = g[x][1].size();
    
    cout << t1 << " ";
    for (int i = 0; i < t1; i ++ )
        cout << g[x][0][i] << " ";
    cout << endl;
    
    cout << t2 << " ";
    for (int i = 0; i < t2; i ++ )
        cout << g[x][1][i] << " ";
    cout << endl;
    
    return;
}

void solve()
{
    cin >> n;
    
    for (int i = 0; i < n; i ++ )
        cin >> a[i];
    
    // 至多枚举前八个a[i]的所有状态
    for (int i = 1; i < 1 << min((int)8, n); i ++ )
    {
        int s = 0;
        vector<int> temp;
        for (int j = 0; j < 8; j ++ )
            if(i >> j & 1)
            {
                s = (s + a[j]) % mod;
                temp.push_back(j + 1);
            }
        g[s].push_back(temp);
    }
    
    // 枚举检查即可
    for (int i = 0; i < 200; i ++ )
        if(g[i].size() >= 2)
        {
            cout << "YES" << endl;
            print(i);
            return;
        }
        
    cout << "NO" << endl;
    
    return;
}

signed main()
{
    T = 1;
    //fast;cin >> T;
    //scanf("%d", &T);
    
    //for (cases = 1; cases <= T; cases ++ )
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103

---

E - 旅行商问题

E - 旅行商问题

思路：

• 旅行商问题（又称：$TSP$ 问题，$travelingsalesmanproblem$）
• 其实就是 $最短Hamilton路径+Floyd算法$

具体实现：

• 最短Hamilton 路径：求最终停在哪个点上
• Floyd算法：求从最终停的点回到起点的最小路径（其他单源最短路算法也可以，此处灵活应变，若 $Dijkstra$ 求 $n$ 次，时间复杂度也是 $O(n^3)$，因为此处是单向边，所以必须倒着求到起点的距离）
• 如此我们知道答案即为两者之和

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define mkpr make_pair
#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 15, M = N * 2;
const int YB = 8, YM = 1e8;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

int f[1 << N][N]; // 经过的点为 i ，且当前点为 j 的路径的最小值
int g[N][N];

void floyd()
{
    for (int k = 0; k < n; k ++ )
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < n; j ++ )
                g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}

void solve()
{
    memset(g, 0x3f, sizeof g);
    
    n ++;
    
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            cin >> g[i][j];
            
    floyd();
    
    memset(f, 0x3f, sizeof f);
    f[1][0] = 0;
    
    // 最短 Hamilton 回路
    for (int i = 0; i < 1 << n; i ++ )
        for (int j = 0; j < n; j ++ )
            if(i >> j & 1)
                for (int k = 0; k < n; k ++ )
                    if(i - (1 << j) >> k & 1)
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + g[k][j]);
    
    // floyd 回到起点 0
    int res = INF;
    for (int i = 1; i < n; i ++ )
        res = min(res, f[(1 << n) - 1][i] + g[i][0]);
        
    cout << res << endl;
    
    return;
}

signed main()
{
    T = 1;
    //fast;cin >> T;
    //scanf("%d", &T);
    
    //for (cases = 1; cases <= T; cases ++ )
    while(cin >> n, n)
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

---

简单小习题：

积木画（蓝桥杯十三届省赛B组）

积木画

思路：

• 状态压缩 $DP$，蒙德里安的梦想的简化版
• 可以手推状态转移

代码如下：

#include 
#include 
#include 

using namespace std;

const int N = 1e7 + 10, mod = 1e9 + 7;

int n, m;

// 0 0
// 0 0

// 集合：所有 第 i - 1 列已经装满，开始装第 i 层，且第 i 列的状态为 j 的方案
// 属性：数量
int f[2][4]; // 滚动数组

int g[4][4] = {
    {1, 1, 1, 1},
    {0, 0, 1, 1},
    {0, 1, 0, 1},
    {1, 0, 0, 0},
};

int main()
{
    cin >> n;
    
    f[1][0] = 1;
    
    for (int i = 1; i <= n; i ++ )
    {
        memset(f[i + 1 & 1], 0, sizeof f[0]);
        for (int j = 0; j < 4; j ++ )
            for (int k = 0; k < 4; k ++ )
                if(g[j][k])
                    f[i + 1 & 1][k] = (f[i + 1 & 1][k] + f[i & 1][j]) % mod;
    }
    cout << f[n + 1 & 1][0] << endl;
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42