-
【算法】链表经典OJ
一. 移除链表元素
题目链接
题目描述
给你一个链表的头节点
head和一个整数val,请你删除链表中所有满足Node.val == val的节点,并返回 新的头节点 。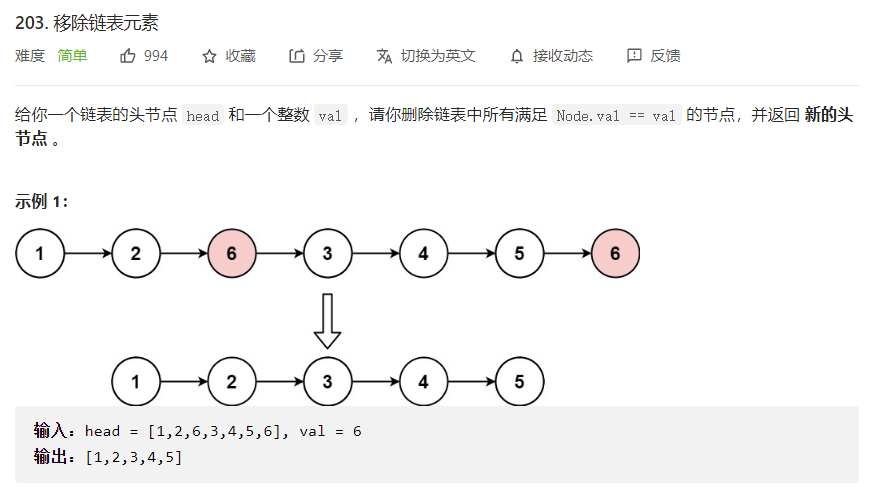
法一:暴力
思路
遍历链表,对比每一个节点的数据与val是否相等,如果相等,就free该节点。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* removeElements(struct ListNode* head, int val){ //assert(head); 不能断言 struct ListNode* cur = head; struct ListNode* prev = NULL; while(cur) { if(cur->val == val) { if(cur == head)//头删,改变头结点 { head= head->next; free(cur); cur = head; } else//非头删 { prev->next = cur->next; free(cur); cur = prev->next; } } else//寻找指定节点 { prev = cur; cur = cur->next; } } return head; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
易错点
1、当链表的头结点的数据等于val时,我们free掉该节点后需要挪动head指针,让其指向新的头结点
2、我们在遍历链表的时候需要记录前一个节点的地址,因为当我们free掉当前节点之后,我们要让前一个节点的next;链接到当前节点的下一个节点
法二
思路
遍历链表,对比每一个节点的数据与val是否相等,如果相等,就free该节点;如果不相等,就尾插到一个新链表。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* removeElements(struct ListNode* head, int val){ //assert(head); 不能断言 struct ListNode* cur = head; struct ListNode* newhead = NULL, *tail = NULL; while(cur) { if(cur->val != val) { if(tail == NULL) { newhead = tail = cur; } else { tail->next = cur; tail = cur; } cur = cur->next; } else { struct ListNode* del = NULL; del = cur; cur = cur->next; free(del); } } if(tail) tail->next = NULL; return newhead; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
易错点
1、当tail走到尾节点的前一个节点,尾节点被我们free掉了,tail此时是尾节点,但是它却指向了被free掉的尾节点,造成野指针问题,这里我们判断一下,如果tail不为空,我们把tail->next置为NULL
1、由于我们是把原链表中的节点尾插到新链表中去,所以我们插入元素的时候需要判断链表是否为空,如果为空,我们需要改变新链表的头结点
法三:双指针
思路
设置两个均指向头节点的指针,prev(记录待删除节点的前一节点)和 cur (记录当前节点);遍历整个链表,查找节点值为 val 的节点,找到即删除该节点,否则继续查找。
找到,将当前节点的前一节点(之前最近一个值不等于 val 的节点(pre))连接到当前节点(cur)的下一个节点(即将 pre 的下一节点指向 cur 的下一节点:pre->next = cur->next);没找到,更新最近一个值不等于 val 的节点(即 pre = cur),并继续遍历(cur = cur->next)。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* removeElements(struct ListNode* head, int val){ while(head != NULL && head->val == val) { head = head->next; } struct ListNode* cur = head; struct ListNode* prev = NULL; while(cur!=NULL) { if(cur->val != val) { prev = cur; } else { prev->next = cur->next; } cur = cur->next; } return head; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21

法四:虚拟头节点(哨兵)
前三种方法均需要判断头节点是否为待删除的节点,且处理头节点的代码逻辑与其它节点特别相似,有没有方法使得代码更优美并且能避免对头节点的判断呢?答案是有的。可以通过在头节点前增加虚拟头节点,这样头节点就成了普通节点,不需要单独拎出来考虑,但是在返回的时候,返回的是虚拟头节点的下一节点而不是虚拟头节点。
思路
遍历链表,对比每一个节点的数据与val是否相等,如果相等,就free该节点;如果不相等,就尾插到一个新链表。这里把我们的新链表设计为带哨兵位的,这样我们直接进行尾插就行,不用判断链表是否为空。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* removeElements(struct ListNode* head, int val){ struct ListNode* guard = (struct ListNode*)malloc(sizeof(struct ListNode)); guard->next = head; struct ListNode* cur = guard; while(cur->next != NULL) { if(cur->next->val != val) { cur = cur->next; } else { struct ListNode* del = cur->next; cur->next = del->next; free(del); } } struct ListNode* retNode = guard->next; free(guard); guard = NULL; return retNode; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22

易错点
1、但是要注意返回的是虚拟头节点的下一节点而不是虚拟头节点,因为虚拟头结点不用于存储数据,同时在return之前记得把虚拟头结点释放掉。
二. 反转链表
题目链接
题目描述
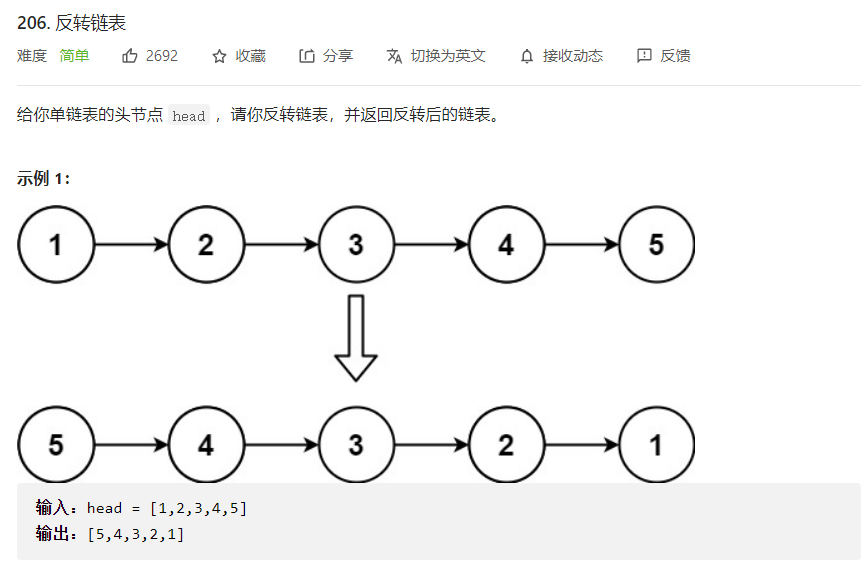
法一:暴力
思路
把原链表的节点头插到新链表中,然后返回新链表的头。假设链表为 1→2→3→NULL,我们想要把它改成 NULL←1←2←3。
在遍历链表时,将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* reverseList(struct ListNode* head){ struct ListNode* cur = head;//当前指针节点 struct ListNode* prev = NULL;//前指针节点 while(cur!=NULL) { struct ListNode* next = cur->next; //临时节点,暂存当前节点的下一节点,用于后移 cur->next = prev; //将当前节点指向它前面的节点 prev = cur;//前指针后移 cur = next;//当前指针后移 } return prev; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15

易错点
如果我们的链表不带头,我们每头插一个元素都需要改变头结点
法二:双指针
思路
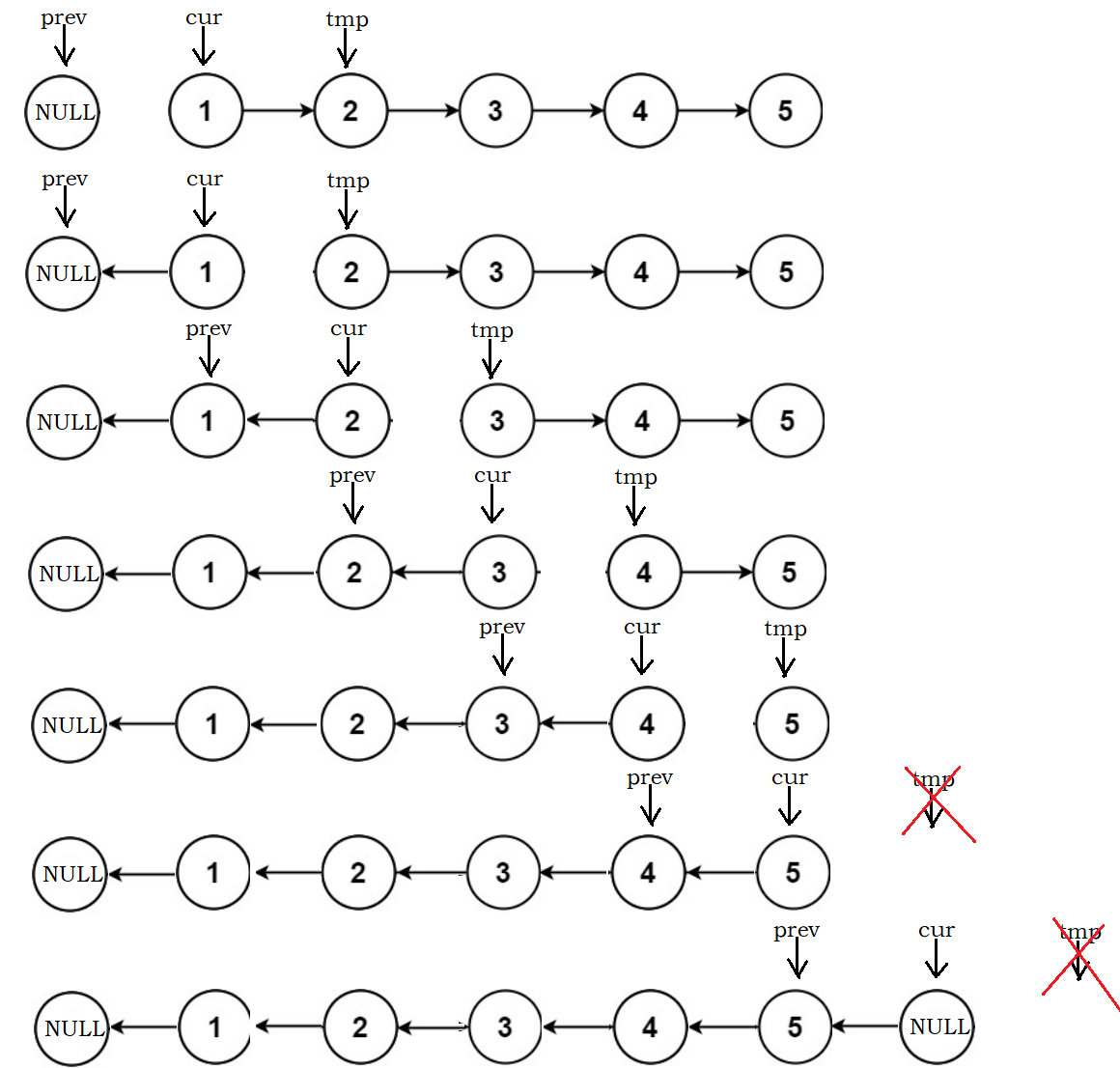
首先定义一个cur指针,指向头结点,再定义一个prev指针,初始化为NULL。
当cur指针指向的元素非空时,重复下列操作:
首先要把 cur->next 节点用 临时的 tmp 指针保存一下,也就是保存一下这个节点。
每次让 prev 的 next 指向 cur ,实现一次局部反转。局部反转完成之后,prev 和 cur 同时往前移动一个位置。循环上述过程,直至 prev 到达链表尾部
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* reverseList(struct ListNode* head){ struct ListNode* cur = head;//当前指针节点 struct ListNode* prev = NULL;//前指针节点 while(cur!=NULL) { struct ListNode* tmp = cur->next; //临时节点,暂存当前节点的下一节点,用于后移 cur->next = prev; //将当前节点指向它前面的节点 prev = cur;//前指针后移 cur = tmp;//当前指针后移 } return prev; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
法三:递归
使用递归函数,一直递归到链表的最后一个结点,该结点就是反转后的头结点,记作 newhead 。此后,每次函数在返回的过程中,让当前结点的下一个结点的 nextnext 指针指向当前节点。同时让当前结点的 nextnext 指针指向 NULLNULL ,从而实现从链表尾部开始的局部反转。当递归函数全部出栈后,链表反转完成。
时间复杂度:O(N),其中 N 是链表的长度。需要对链表的每个节点进行反转操作。
空间复杂度:O(N),其中 N 是链表的长度。空间复杂度主要取决于递归调用的栈空间,最多为 N 层。
/* 递归法反转链表 */ struct ListNode* reverseLinkedList(struct ListNode* head) { if (head == NULL || head->next == NULL) { return head; } struct ListNode* newhead = reverseLinkedList(head->next); head->next->next = head; head->next = NULL; return newhead; } /** * 以链表1->2->3->4->5举例 */ struct ListNode* reverseLinkedList(struct ListNode* head) { if (head == NULL || head->next == NULL) { /* 直到当前节点的下一个节点为空时返回当前节点 由于5没有下一个节点了,所以此处返回节点5 */ return head; } //递归传入下一个节点,目的是为了到达最后一个节点 struct ListNode* newhead = reverseLinkedList(head->next); /* 第一轮出栈,head为5,head.next为空,返回5 第二轮出栈,head为4,head.next为5,执行head.next.next=head也就是5.next=4, 把当前节点的子节点的子节点指向当前节点 此时链表为1->2->3->4<->5,由于4与5互相指向,所以此处要断开4.next=null 此时链表为1->2->3->4<-5 返回节点5 第三轮出栈,head为3,head.next为4,执行head.next.next=head也就是4.next=3, 此时链表为1->2->3<->4<-5,由于3与4互相指向,所以此处要断开3.next=null 此时链表为1->2->3<-4<-5 返回节点5 第四轮出栈,head为2,head.next为3,执行head.next.next=head也就是3.next=2, 此时链表为1->2<->3<-4<-5,由于2与3互相指向,所以此处要断开2.next=null 此时链表为1->2<-3<-4<-5 返回节点5 第五轮出栈,head为1,head.next为2,执行head.next.next=head也就是2.next=1, 此时链表为1<->2<-3<-4<-5,由于1与2互相指向,所以此处要断开1.next=null 此时链表为1<-2<-3<-4<-5 返回节点5 出栈完成,最终头节点5->4->3->2->1 */ head->next->next = head; head->next = NULL; return newhead; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
三. 链表的中间节点
题目链接
题目描述
法一:暴力
思路
遍历两遍链表,第一遍求出链表长度,第二步找出链表的中间节点并返回。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* middleNode(struct ListNode* head){ struct ListNode* cur = head; int count = 0; while(cur!=NULL) { cur = cur->next; count++; } cur = head; count/=2; while(count--) { cur = cur->next; } return cur; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

法二:双指针
思路
法一十分简单,但是如果要求只能遍历一遍链表;这时候就只能用快慢指针来解题了。考虑借助快慢双指针 fast, slow 。快指针 fast每轮走 2 步,慢指针 slow每轮走 1 步。fast 的步数恒为 slow 的 2 倍,因此当快指针遍历完链表时,慢指针就指向链表中间节点。而由于长度为偶数的链表有两个中间节点,因此需要分两种情况考虑:
链表长度为奇数: 当 fast 走到链表尾节点时,slow 正好走到中间节点。
链表长度为偶数: 当 fast 走到NULL时(越过尾节点后),slow 正好走到第二个中间节点。
总结以上规律,应在当 fast 遇到或越过 尾节点 时跳出循环,并返回 slow 即可。时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* middleNode(struct ListNode* head){ struct ListNode* fast = head; struct ListNode* slow = head; while(fast != NULL && fast->next != NULL) { fast = fast->next->next; slow = slow->next; } return slow; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10

易错点
注意我们在写while循环的条件时,必须写成fast&&fast->next,不能写成fast->next&&fast,因为当链表长度为偶数是,后面这种写法会发生空指针的解引用问题。
四. 链表中倒数第K个节点
题目链接
链表中倒数第k个结点_牛客题霸_牛客网 (nowcoder.com)
题目描述
法一:暴力
思路
也是遍历两遍链表,第一遍求出链表长度,第二步找出链表的倒数第K个节点并返回。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) { // write code here struct ListNode* cur = pListHead; int count = 0; if(cur==NULL) { return NULL; } while(cur!=NULL) { count++; cur = cur->next; } if(k > count | k <= 0) { return NULL; } int m = count - k; cur = pListHead; for(int i = 0; i < m; i++) { cur = cur->next; } return cur; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
易错点
1、首先检查是否链表为空,为空直接返回
2、其次检查K是否大于链表的长度及K是否小于等于0,造成访问越界
法二:双指针
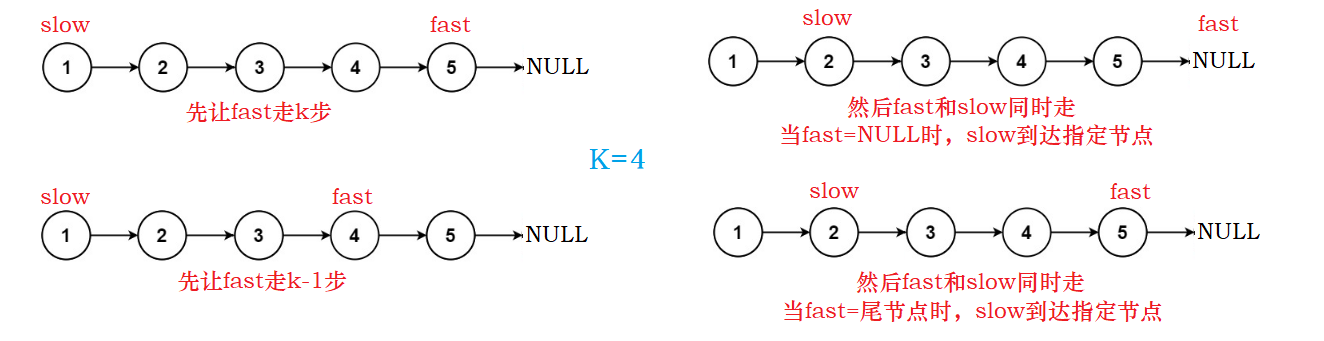
我们发现法一的时间复杂度比较高,代码太挫了。如果要求链表只能遍历一遍,就玩完了。这里我们依然可以用我们的快慢指针做。双指针yyds!!! 我们定义两个指针,快指针——fast,慢指针——slow。我们主要是找规律,以快指针走到null停下为例:快指针停在NULL,慢指针刚好停在倒数第K个结点。此时它俩的距离是K,所以我们设置慢指针开始走的条件应该是快指针走了K步之后。第K+1步的时候,快慢指针一起走。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) { // write code here struct ListNode* fast = pListHead; struct ListNode* slow = pListHead; while(k--) { if(fast==NULL) return NULL; fast =fast ->next; } while(fast!=NULL) { fast = fast->next; slow = slow->next; } return slow; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
易错点
1、当K大于链表长度时,如果我们在K-- 的 while 循环中没有对 fast 进行空指针检查的话,那么 fast 会不断往后走,直到 fast == NULL 时仍然不会停下,这时候就会造成对空指针解引用的问题。
2、当plistHead = NULL时,程序也会出现问题,因为fast检查是否NULL时,第一次就避免了空指针的问题。但是if(fast==NULL) return NULL;必须放在 fast =fast ->next;前面。
五. 合并两个有序链表
题目链接
题目描述
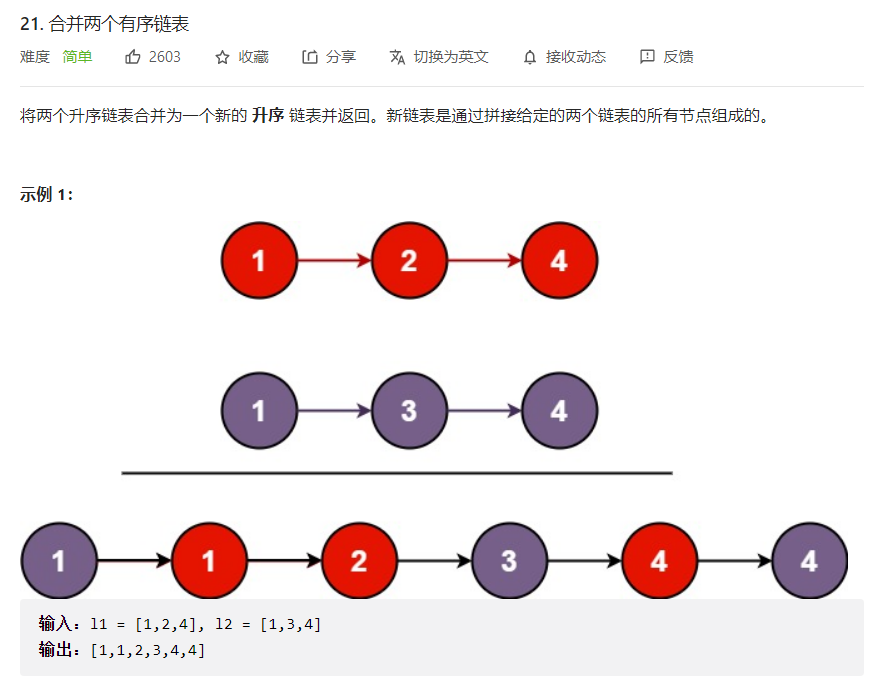
法一:迭代
思路
这道题是不是很熟悉,这道题和顺序表中的合并两个有序数组的思路一模一样,不过这里尾插的是节点。
这里我们是把原来链表中的节点尾插到新链表中去,所以我们插入元素的时候需要判断链表为啥为空,如果为空,我们需要改变新链表的头结点。不过我们可以把我们的新链表设计为带哨兵位头的,我们就可以直接进行尾插。
时间复杂度:O(m+n) 其中 n 和 m 分别为两个链表的长度。
空间复杂度:O(1)
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2){ struct ListNode* cur = (struct ListNode*)malloc(sizeof(struct ListNode)); cur->next = NULL; struct ListNode* prev = cur; while(list1&&list2) { if(list1->val > list2->val) { cur->next = list2; list2 = list2->next; } else { cur->next = list1; list1 = list1->next; } cur = cur->next; } if(list1) cur->next = list1; if(list2) cur->next = list2; struct ListNode* head = prev->next; free(prev); return head; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26

易错点
1、当其中的一个链表指向NULL,另一个链表一定不为NULL,可能有一个元素,也可能有多个元素,所以我们在结尾判断哪一个链表不为空,然后再把它链接起来。
法二:递归
思路
终止条件:当两个链表都为空时,表示我们对链表已合并完成。
如何递归:我们判断 list1 和 list2 头结点哪个更小,然后较小结点的 next 指针指向其余结点的合并结果。(调用递归)递归较难理解,所以可以看下注释代码中的递归调用全过程。
时间复杂度:O(n + m),其中 n 和 m 分别为两个链表的长度。因为每次调用递归都会去掉 list1 或者 list2 的头节点(直到至少有一个链表为空),函数 mergeTwoList 至多只会递归调用每个节点一次。因此,时间复杂度取决于合并后的链表长度,即 O(n + m)。
空间复杂度:O(n + m),其中 n 和 m 分别为两个链表的长度。递归调用 mergeTwoLists 函数时需要消耗栈空间,栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n + m 次,因此空间复杂度为 O(n + m)。
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2){ //如果比较到最后,list1为空,那就返回list2指向剩下的那些元素 if(list1 == NULL) { return list2;//这是递归的出口 } else if(list2 == NULL) { return list1;//这是递归的出口 } else if(list1->val < list2->val) //这步操作就是找出最小的那个(当前是list1->val最小),然后继续比较后续两个链表中的元素 //list1->next就是指向后续比较出最小的元素 { list1->next = mergeTwoLists(list1->next, list2); //每次比较完,需要返回第一个节点的地址,以便最后递归结束,从后往前返回地址,连接起来 return list1; } else { list2->next = mergeTwoLists(list1, list2->next); return list2; } } //这里的两个链表分别为1->4->5->null, 1->2->3->6->null // (1,1):代表第一次进入递归函数,并且从第一个口进入,并且记录进入前链表的状态 // mergeTwoLists(1,1): 1->4->5->null, 1->2->3->6->null // mergeTwoLists(2,2): 4->5->null, 1->2->3->6->null // mergeTwoLists(3,2): 4->5->null, 2->3->6->null // mergeTwoLists(4,2): 4->5->null, 3->6->null // mergeTwoLists(5,1): 4->5->null, 6->null // mergeTwoLists(6,1): 5->null, 6->null // mergeTwoLists(7): null, 6->null // return list2 // list1->next --- 5->6->null, return list1 // list1->next --- 4->5->6->null, return list1 // list2->next --- 3->4->5->6->null, return list2 // list2->next --- 2->3->4->5->6->null, return list2 // list2->next --- 1->2->3->4->5->6->null, return list2 // list1->next --- 1->1->2->3->4->5->6->null, return list1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40

六. 链表分割
题目链接
题目描述
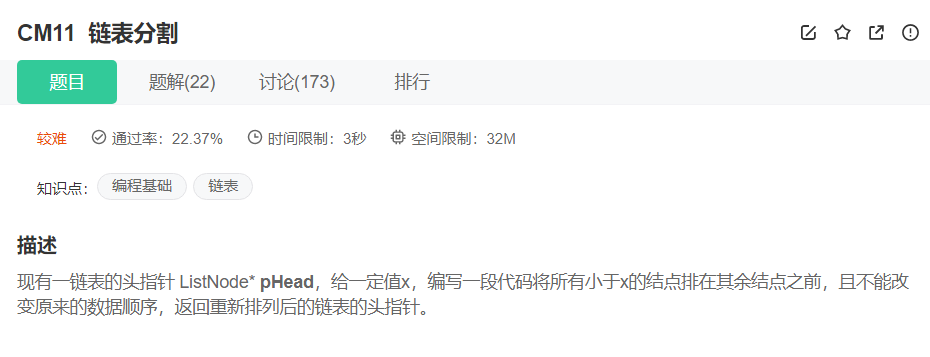
法一
思路
将原链表中val小于x的节点尾插到一个新链表中,将val大于x的节点尾插到另一个新链表中,最后将两个新链表链接起来。
时间复杂度:O(N) 空间复杂度:O(1)
class Partition { public: ListNode* partition(ListNode* pHead, int x) { // write code here struct ListNode* lesstail, *greatertail, *lessguard, *greaterguard; lessguard = lesstail = (struct ListNode*)malloc(sizeof(struct ListNode)); greaterguard = greatertail = (struct ListNode*)malloc(sizeof(struct ListNode)); greatertail->next = lesstail->next = NULL;//空链表处理 struct ListNode* cur = pHead; while(cur) { if(cur->val < x) { lesstail->next = cur; lesstail = lesstail->next; } else { greatertail->next = cur; greatertail = greatertail->next; } cur = cur->next; } lesstail->next = greaterguard->next; greatertail->next = NULL;//链表成环问题 pHead = lessguard->next; free(greaterguard); free(lessguard); return pHead; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
易错点
1、我们可以将两个新链表设计为带头链表,这样可以免去插入第一个元素时的判断步骤,避免犯错;
2、我们需要将用于链接val大于x的链表的尾结点的next置空,避免最后一个节点的val小于x时前一个节点的next仍指向它,从而形成环
七. 链表的回文结构
题目链接
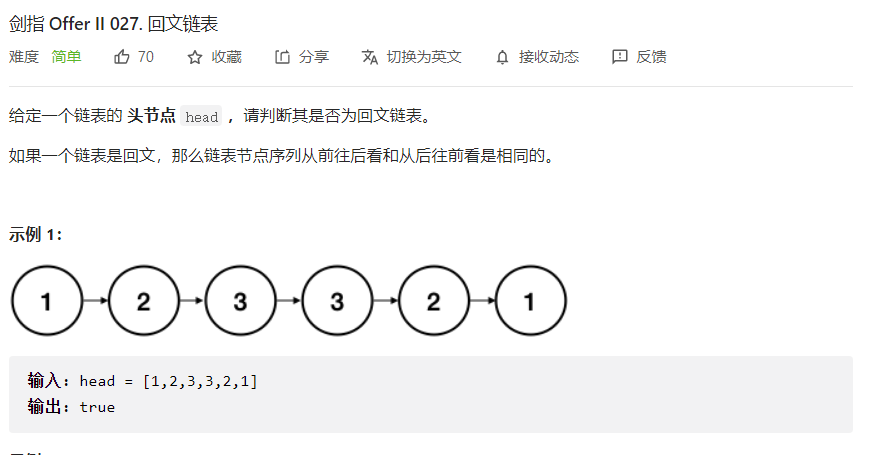
剑指 Offer II 027. 回文链表 - 力扣(LeetCode)
题目描述
法一:组合拳
思路
回文链表,也就是从链表的头节点往后看和尾节点往前看是相同的。
因此要判断链表是否是回文链表,可以考虑把链表反转,然后再判断反转后的链表是否跟原链表完全一样。
实际上,没有必要把链表全部反转,因为回文就意味着对称,因此只需要找到链表的中间节点,把中间节点后面的链表反转即可。
方法:找中间节点 + 反转链表 + 遍历链表
找中间节点和反转链表的函数,我们在前面都实现过,直接偷家吧(拿来吧你)。
遍历链表判断链表的前半部分与反转后的后半部分是否相同,需要注意节点不能为空(否则不能对 head 取 head->val)。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode* reverseList(struct ListNode* head){ struct ListNode* cur = head;//当前指针节点 struct ListNode* prev = NULL;//前指针节点 while(cur!=NULL) { struct ListNode* next = cur->next; //临时节点,暂存当前节点的下一节点,用于后移 cur->next = prev; //将当前节点指向它前面的节点 prev = cur;//前指针后移 cur = next;//当前指针后移 } return prev; } struct ListNode* middleNode(struct ListNode* head){ struct ListNode* fast = head; struct ListNode* slow = head; while(fast != NULL && fast->next != NULL) { fast = fast->next->next; slow = slow->next; } return slow; } bool isPalindrome(struct ListNode* head) { // write code here struct ListNode* mid, *rmid; mid = middleNode(head); rmid = reverseList(mid); while(head && rmid) { if(head->val != rmid->val) return false; head = head->next; rmid = rmid->next; } return true; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41

法二:暴力
思路
把链表每个节点的值存进数组,再双指针从左右两边向中间走比较两个值,若遍历过程中比较的两个值不同则不是回文,遍历完都相等则是回文。简单是简单,就是效率太低。
时间复杂度:O(N) 空间复杂度:O(N)
int listSize(struct ListNode *head) { int sz = 0; while (head) { sz++; head = head->next; } return sz; } bool isPalindrome(struct ListNode* head){ if (head == NULL || head->next == NULL) { return true; } int sz = listSize(head); int *arr = (int *)malloc(sizeof(int) * sz); for (int i = 0; i < sz; i++) { arr[i] = head->val; head = head->next; } for (int i = 0, j = sz - 1; i <= j; i++, j--) { if (arr[i] != arr[j]) { return false; } } return true; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34

八. 相交链表
题目链接
题目描述
法一
思路
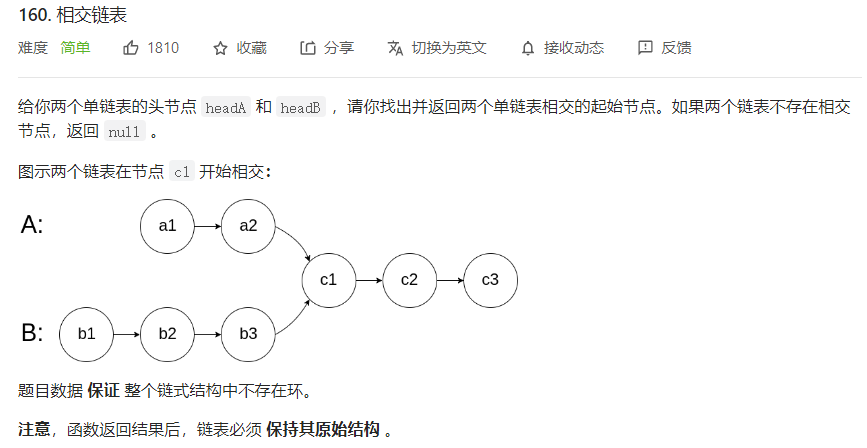
相交链表从相交的节点开始,后面的节点都是相同的,即相交链表的尾结点一定是相同的;所以我们可以先求出两个链表的长度,让较长的链表先走差距步;然后遍历两个链表,两个链表的节点地址相同处就是相交的起始节点。
时间复杂度:O(N) 空间复杂度:O(1)
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) { if(headA == NULL||headB == NULL) return NULL; struct ListNode* curA = headA, *curB = headB; int lenA = 0, lenB = 0; //求出两个节点的长度 while(curA) { curA = curA->next; lenA++; } while(curB) { curB = curB->next; lenB++; } //长度不相同,直接返回空 if(curA != curB) return NULL; struct ListNode* longlist = headA,*shortlist = headB; if(lenA < lenB) { longlist = headB; shortlist = headA; } int gap = abs(lenA-lenB); //让长度较长的链表先走差距步 while(gap--) { longlist = longlist->next; } //从longlist位置处往后遍历链表,第一个相同地址的节点就是相交的起始节点 while(longlist != shortlist) { longlist = longlist->next; shortlist = shortlist->next; } return longlist; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40

易错点
由于两个链表的长度不一定是相同的,所以我们不能直接对比两个链表的节点地址,这样会发生错位,而是应该先让两个链表对齐。
法二:双指针
思路
定义两个指针,一个pA,一个pB,pA和pB同时走,pA走过的路径为A链+B链,pB走过的路径为B链+A链。
pA和pB走过的长度都相同,都是A链和B链的长度之和,相当于将两条链从尾端对齐,如果相交,则会提前在相交点相遇,如果没有相交点,则会在最后相遇。从数学公式上理解:若相交,链表A: a+c, 链表B : b+c。 a+c+b+c = b+c+a+c 。则会在公共处c起点相遇。若不相交,a +b = b+a 。因此相遇处是NULL
时间复杂度:O(m+n),m、n分别是两个链表的长度。 空间复杂度:O(1)
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) { if (headA == NULL || headB == NULL) { return NULL; } struct ListNode *pA = headA, *pB = headB; while (pA != pB) { pA = pA == NULL ? headB : pA->next; pB = pB == NULL ? headA : pB->next; } return pA; } //pA:1->2->3->4->5->6->null->9->5->6->null //pB:9->5->6->null->1->2->3->4->5->6->null //相遇处为节点5- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14

九. 环形链表
题目链接
题目描述
法一:双指针
思路
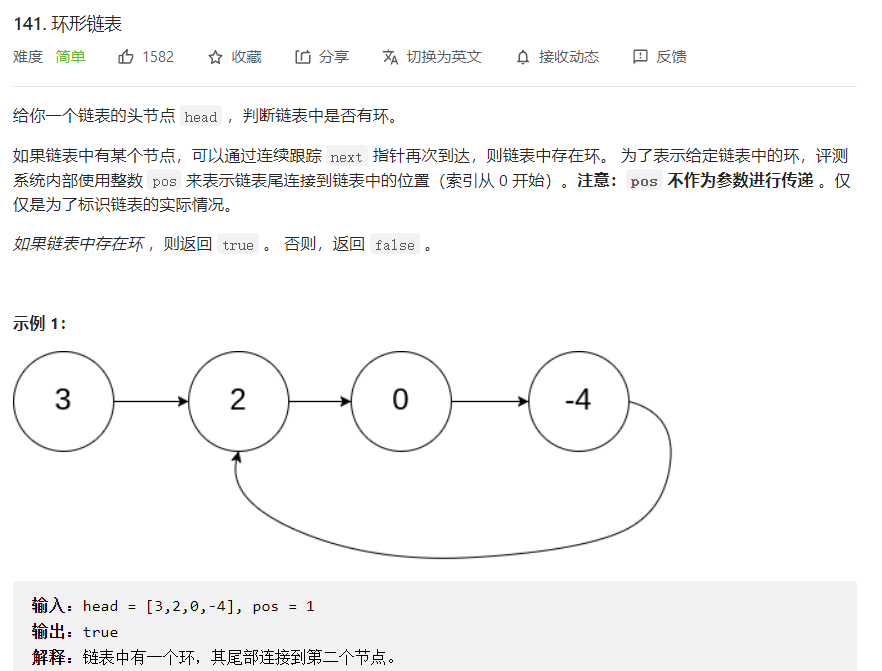
用两个指针,初始位置都指向链表头节点。每次快指针向后移动两个节点,慢指针向后移动一个节点。如果快指针移动到了链表尾部,就说明链表无环如果快慢指针相遇了,就说明链表有环。
**注意:**若有环,则快慢指针一定会相遇。因为快指针一定比慢指针提前进入到环中,等慢指针也进入环中后,快指针一定会追上满指针(因为速度是慢指针的两倍),并且一定不会不相遇而直接跳过去。
时间复杂度O(N),其中 n 是链表中节点的个数。慢指针的速度是快指针的一半,快指针会在两圈内追上慢指针。
空间复杂度O(1)bool hasCycle(struct ListNode *head) { struct ListNode* fast, *slow; fast = slow = head; while(fast && fast->next) { fast = fast->next->next; slow = slow->next; if(fast == slow) return true; } return false; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
拓展问题
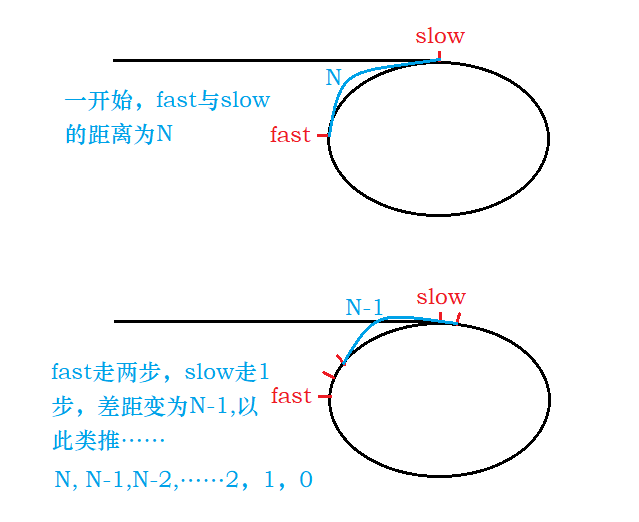
(1)slow一次走1步,fast一次走2步,一定能追上吗?
答案:一定能。
假设链表带环,两个指针最后都会进入环,快指针先进环,慢指针后进环。当慢指针刚进环时,可能就和快指针相遇了,最差情况下两个指针之间的距离刚好就是环的长度。此时,两个指针每移动一次,之间的距离就缩小一步,不会出现每次刚好是套圈的情况,因此:在满指针走到一圈之前,快指针肯定是可以追上慢指针的,即相遇。
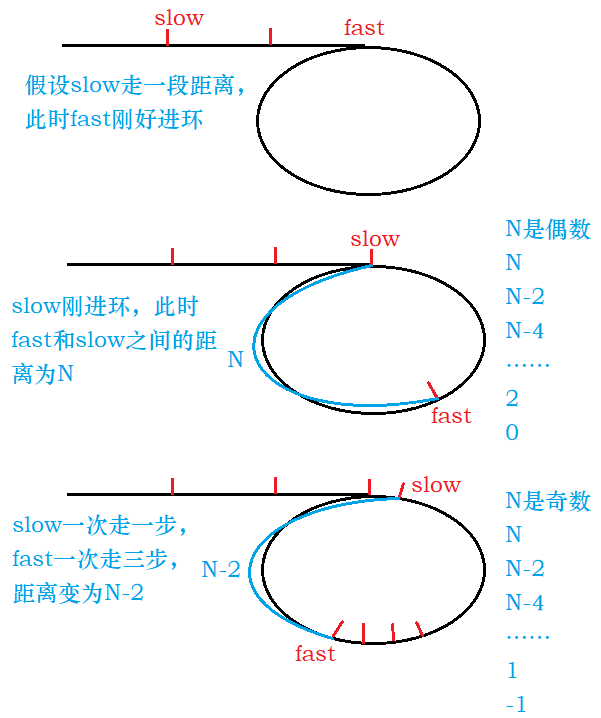
(2)slow一次走1步,fast一次走3步,能追上吗?fast一次走4步呢?n步呢?
答案:不一定。
我们先来讨论slow一次走1步,fast一次走3步的情况。假设slow走了1步,fast走3步时刚好进环,而当slow刚好进环的时候,fast可能已经走了1圈,具体情况得看环的大小,此时slow和fast之间的距离为N。并假设环的长度是C。
slow一次走1步,fast一次走3步,距离变为N-2。由此可见,fast和slow每走一次,距离缩短2。此时就不难发现了,需要分类讨论,当N是偶数时,刚好可以追上,当N是奇数时,追到最后距离为-1,此时就要再追了,意味着slow和fast之间的距离变成C-1。
继续追击,根据前面的分析,如果C-1是偶数,那么可以追上。如果C-1是奇数,那么就永远追不上了,将会无限循环追下去,可就是追不上。他们的差距N是由进环前的长度和环的长度决定的,而这两个又都是随机的,所以N的值不确定,可奇可偶,又像刚刚那样讨论下去,出现奇数永远追不上。
(3)链表环的入口点在哪呢?在下一题。
十. 环形链表II
题目链接
题目描述
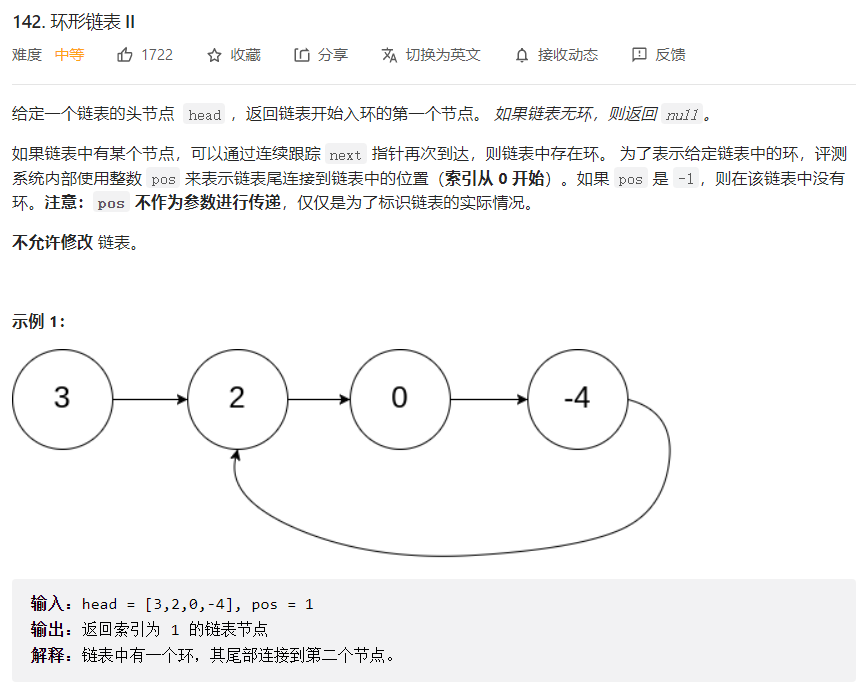
法一:公式法
思路
结论法:定义两个指针 – fast 和 slow,快指针一次走两步,慢指针一次走一步,首先求出二者在环中的相遇点;然后一个指针从链表的头开始走,另一个指针从相遇点开始走,最终二者会在入环点相遇。
时间复杂度:O(N) 空间复杂度:O(1)
(3)链表环的入口点在哪呢?
当我们搞清楚slow和fast分别走的距离时,入口点自然就明了了。
slow一次走1步,fast一次走2步,那么fast走的距离是slow的2倍。
在具体讲解之前,首先要搞清楚,不存在说慢指针slow在里头走了一圈,快指针fast还没有追到slow,因为fast每次走2步,slow每次走1步,它俩间的距离每次都缩小1,所以只会越来越近,直到追到。最多最多也就快1圈,但从来也不会刚好满1圈。所以下面很容易推出slow和fast分别走了多少。
假设:
【链表头 - - - 入口点】:L
【入口点 - - - 相遇点】:X
【环的长度】:R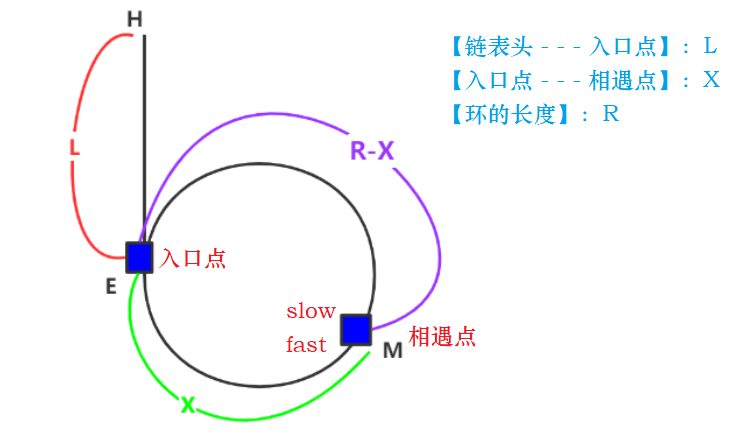
slow走的距离:L + Xfast走的距离:L + N*R + X
解释:
因为先前已经提到slow不会都走了一圈还没被追到,所以很容易推出slow的距离就是L+X而快指针一次走2步,很可能会因为环过小导致在slow指针进入入口点前,fast指针已经走了好几圈。
总结出三种情况:
L很小,C很大,slow进环前,fast可能在环里面,一圈都没走完
L很大,C很小,slow进环前,fast在里面走了很多圈了
但是slow进环以后,在一圈之内,fast一定追到slow,它们的距离最多C-1
根据一开始说的,fast走的距离是slow走的距离的2倍,可列出如下式子:2 * (L + X) = L + N * C + X
化简后:L+X = N * C 或 L = N * C - X 或 L = (N - 1) C + (C - X) 或 L + X = N * C*
用此公式即可证明:一个指针从meet走,一个指针从head走,他们会在入口点相遇!
//法一:公式结论法--一个指针从链表的头开始走,另一个指针从相遇点开始走,二者最终会在入环点相遇 struct ListNode *detectCycle(struct ListNode *head) { struct ListNode* fast = head, *slow = head, *cur = head; while(fast && fast->next) { //迭代 slow = slow->next; fast = fast->next->next; //找到相遇的节点 if(fast == slow) { struct ListNode* meet = slow; //一个指针从头开始走,另一个指针从相遇点开始走 while(cur != meet) { cur = cur->next; meet = meet->next; } return cur; //二者最终会在入环点相遇 } } return NULL; //无环 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
法二
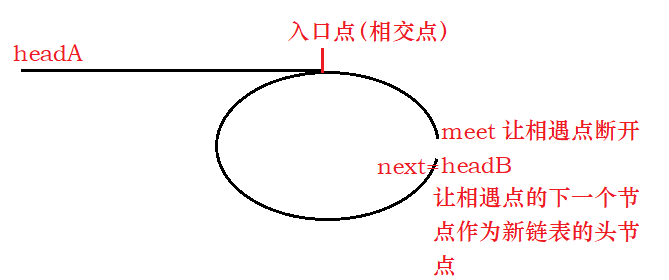
思路:
找到相遇点meet后,让meet做尾,让下一个点做新链表的头,这个方法非常巧妙,刚好转换成了两个链表求交点的问题。因为此时headA链表的尾部是meet,而headB链表的尾部也是meet,此时就意味着俩链表必会相交,而相交的地方就是入口点,两链表相交正是上面所详细讲解的,这里就不赘述了。
时间复杂度:O(N^2) 空间复杂度:O(1)
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) { if(headA == NULL||headB == NULL) return NULL; struct ListNode* curA = headA, *curB = headB; int lenA = 0, lenB = 0; //求出两个节点的长度 while(curA) { curA = curA->next; lenA++; } while(curB) { curB = curB->next; lenB++; } //长度不相同,直接返回空 if(curA != curB) return NULL; struct ListNode* longlist = headA,*shortlist = headB; if(lenA < lenB) { longlist = headB; shortlist = headA; } int gap = abs(lenA-lenB); //让长度较长的链表先走差距步 while(gap--) { longlist = longlist->next; } //从longlist位置处往后遍历链表,第一个相同地址的节点就是相交的起始节点 while(longlist != shortlist) { longlist = longlist->next; shortlist = shortlist->next; } return longlist; } //法二:转换法--把环的入口问题转换为环的相交问题,即把链表从相遇点断开,一个指针从头开始走,一个指针从相遇点后面一个节点开始走,求二者相交 struct ListNode *detectCycle(struct ListNode *head) { struct ListNode* slow = head, *fast = head, *cur = head; while(fast && fast->next) { //迭代 slow = slow->next; fast = fast->next->next; //找到相遇点 if(slow == fast) { //记录相遇点的下一个节点,并把链表从相遇点断开,避免求相交的时候发生死循环 struct ListNode* meet = fast; struct ListNode* next = meet->next; meet->next = NULL; //求两个链表相交 struct ListNode* intersection = getIntersectionNode(cur, next); return intersection; //恢复原链表 meet->next = next; } } return NULL; //无环 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68

十一. 复制带随机指针的链表
题目链接
138. 复制带随机指针的链表 - 力扣(LeetCode)
题目描述

法一:暴力
思路
定义一个指针cur指向原链表第一个元素,cur指向第一个值为7,再malloc出一个7来,cur往后走,继续malloc,再尾插,以此遍历下去。新的链表复制出来了,关键在于如何处理新链表的random指针,这里可以采用找相对距离的方法,找原链表random指向第几个,那么新链表对应指向第几个。总结下来三步:1、拷贝原链表的每个节点;2、得到原链表中每个节点的random指针指向的节点在链表中的相对位置;3、让新链表中每个节点的random指针指向处于相对位置的节点。方法有点复杂,时间复杂度达到了O(N^2),不太推荐。
时间复杂度:O(N^2) 空间复杂度:O(N)
//拷贝节点 struct Node* CopyNode(struct Node* cur) { struct Node* copy = (struct Node*)malloc(sizeof(struct Node)); copy->next = NULL; copy->val = cur->val; copy->random = NULL; return copy; } //法一:1、拷贝原链表的每个节点;2、得到原链表中每个节点的random指针指向的节点在链表中的相对位置;3、让新链表中每个节点的random指针指向处于相对位置的节点 struct Node* copyRandomList(struct Node* head) { struct Node* cur = head; struct Node* newhead = NULL, *tail = NULL, *copy = NULL; //拷贝节点 while(cur) { //如果是复制第一个节点,需要改变头 if(tail == NULL) { copy = CopyNode(cur); newhead = tail = copy; } else { copy = CopyNode(cur); tail->next = copy; tail = tail->next; } //迭代 cur = cur->next; } //得到原链表中每个节点的random指针指向的节点在链表中的相对位置;并让新链表中每个节点的random指针指向处于相对位置的节点 cur = head; struct Node* copycur = newhead; while(cur && copycur) { int count = 0; struct Node* cur1 = head; //找到cur节点的random指针指向的节点在链表中的相对位置 while(cur->random != cur1) { count++; cur1 = cur1->next; } struct Node* copycur1 = newhead; //让copycur中每个节点的random指针指向处于相对位置的节点 while(count--) { copycur1 = copycur1->next; } copycur->random = copycur1; //迭代 cur = cur->next; copycur = copycur->next; } return newhead; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65

法二
1.把拷贝节点链接在原节点后面
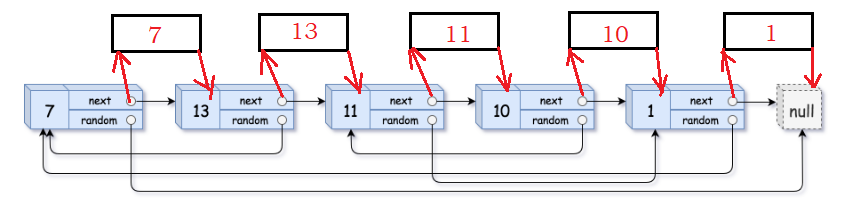
2.接着,链接拷贝节点的random在原节点random后面。比如我们拷贝出来的13这个数字,拷贝的13的random就是原头13的random的next 。因为在原链表中,13的random指向7,现在想让拷贝出来的13的random指向拷贝出来的7。原链表中,7的next指向拷贝出的7,综上:拷贝的13的random就是原头13的random的next 。以此类推。
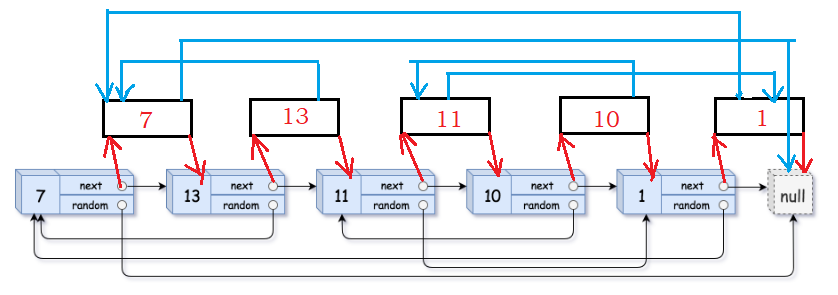
3.将拷贝节点从原链表中分离出来,尾插到新链表中,并修复原链表中各节点的链接关系。
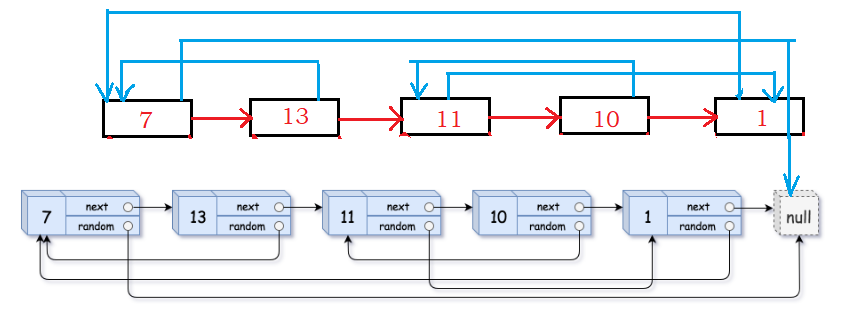
时间复杂度:O(N) 空间复杂度:O(N)
易错点
1、由于我们是直接把拷贝节点链接到了原节点的后面,所以我们一定要注意链接关系的正确修改;并且迭代的时候我们需要让cur指向拷贝节点的下一个节点,即copy->next,而不是指向原节点的下一个节点,即cur->next;
2、在法一中,当原节点的random为NULL时,寻找相对位置的while循环会一直执行,直到cur1走到链表尾结点的下一个节点(NULL),此时count为链表长度+1;然后新链表会把count处节点的地址(NULL)赋给对应节点的random,此时逻辑是正常的;
但是在法二中,当我们节点的random为NULL时,cur->random->next就会造成空指针解引用问题,所以这里我们需要对random为空的情况单独处理,需要特别注意,非常容易错;
3、由于我们在拷贝节点的时候就已经让尾结点的拷贝节点的next指向尾结点的next (NULL) 了,所以我们将拷贝节点插入到新链表中时不用特意将最后一个拷贝节点的next置空。
//拷贝节点 struct Node* CopyNode(struct Node* cur) { struct Node* copy = (struct Node*)malloc(sizeof(struct Node)); copy->next = NULL; copy->val = cur->val; copy->random = NULL; return copy; } //法二:1、将所有拷贝的节点链接到原节点的后面;2、将原节点的random指针指向节点的下一个节点赋给拷贝节点的random;3、将拷贝节点从原链表中分离出来,尾插到新链表中,并修复原链表中各节点的链接关系 struct Node* copyRandomList(struct Node* head) { struct Node* cur = head, *copy = NULL, *next = NULL; struct Node* newhead = NULL, *tail = NULL; //1、将所有拷贝的节点链接到原节点的后面 while(cur) { //拷贝节点、修改链接关系 copy = CopyNode(cur); next = cur->next; cur->next = copy; copy->next = next; //迭代 cur = copy->next; } //2、将原节点的random指针指向节点的下一个节点赋给拷贝节点的random; cur = head; while(cur) { copy = cur->next; //原节点的random指针指向节点的下一个节点就是copy的random需要指向的节点 //这里需要判断cur的randon是否为空,为空就不能进行random->next操作 if(cur->random == NULL) copy->random = NULL; else { copy->random = cur->random->next; cur = copy->next; } //迭代 cur = copy->next; } //3、将拷贝节点从原链表中分离出来,尾插到新链表中,并修复原链表中各节点的链接关系 cur = head; while(cur) { copy = cur->next; //尾插第一个节点时,需要改变头 if(tail == NULL) { newhead = tail = copy; cur->next = copy->next; //修复原链表的链接关系 } else { tail->next = copy; tail = tail->next; cur->next = copy->next; } //迭代 cur = copy->next; } return newhead; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69

-
相关阅读:
【Python开发】Flask开发实战:个人博客(三)
TDengine 连接器上线 Google Data Studio 应用商店
黑马程序员spring+springMVC+Maven高级+springboot+MyBatisPlus总结之SpringMvc参数传递
[SpringMVC笔记] SpringMVC-15-SSM整合-项目异常处理
Spring教程-01-IOC控制反转
Python编程 元组的创建
如何分析软件测试中发现的Bug!
zabbix中文乱码解决方法
nginx的正则回溯和灾难性回溯
Linux学习的五个台阶
- 原文地址:https://blog.csdn.net/m0_64224788/article/details/126547381
