[datawhale202208]计算之魂共读：怎样寻找最好的算法

结论速递

本次通过了解总和最大区间问题（即最大子序和）的四种时间复杂度的求解方法，直观地了解了算法复杂度和最优算法的关系。
同时，了解了对优化算法复杂度的判断包含三个内容：对问题边界的认知，对无用功的判断，以及逆向思维。

前情回顾

1. 算法规范化，大数和数量级的概念

1 怎样寻找最好的算法

1.1 阅读归纳思维导图

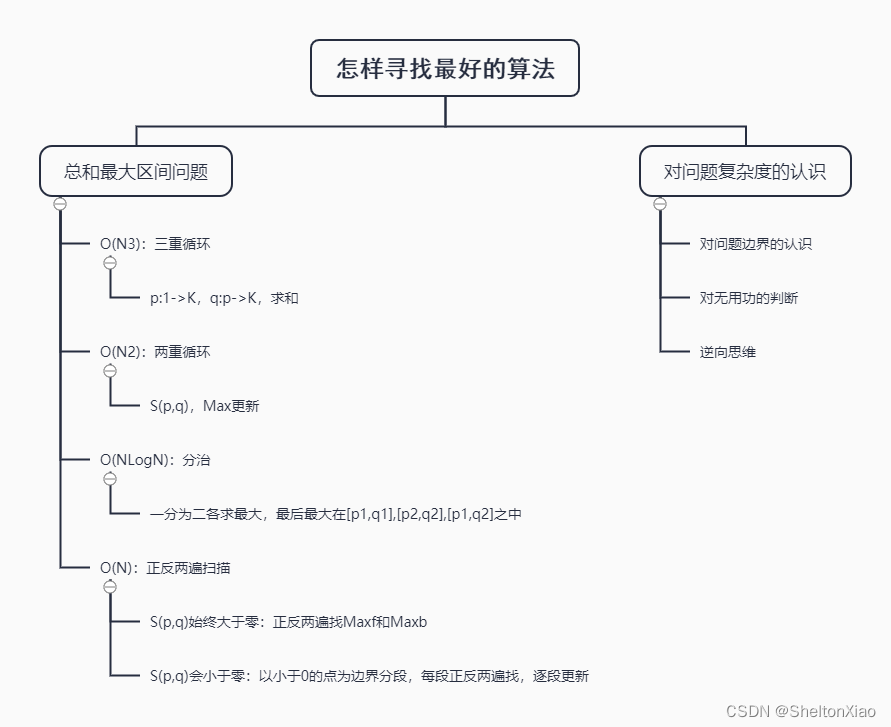
1.2 关键内容总结

1. 总和最大区间问题
   其实对应最大子序列和问题

   • 分治算法
     把序列分成两块计算，用递归分别求出两块序列中的最大子序列和，然后从序列中间向两边遍历求出包含中心的序列的最大和。返回最大的那个序列和。
   • 正反两遍扫描
     对每个使S(p,q)<0的节点划分区间，对每个区间，找Maxf和Maxb，记为l，r。可证，最大区间是在各个区间的Max之间的，不会跨区间。
     
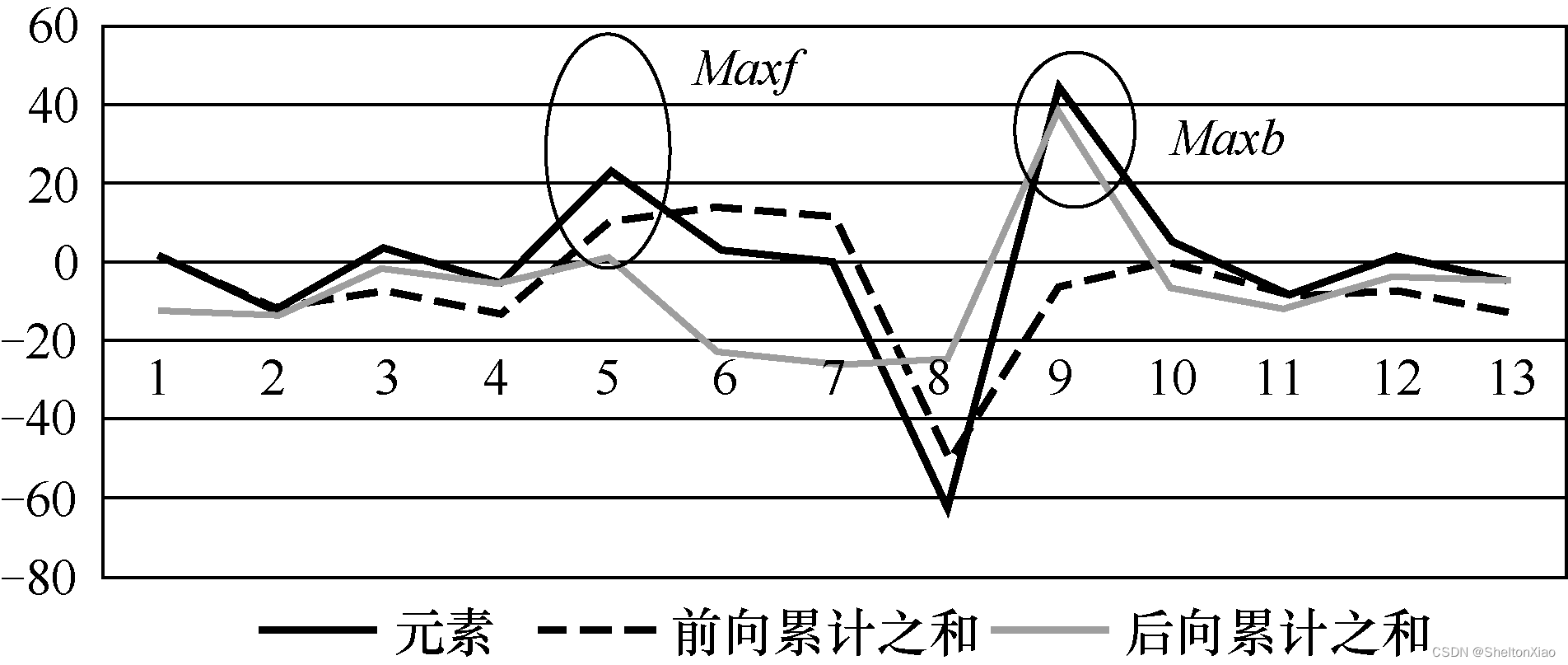
     实现方式如下：
     遍历序列的时候对Sum进行累计，如果Sum累积后小于0的话就把Sum重置为负无穷，每次更新Sum的最大值。最后便能求出最大值。

2. 对问题复杂度的认识
   以上面这道题为例，

   • 对问题边界的认识
     因为要求和，所以至少会是O(n)。
   • 对无用功的判断
     扫描和加法若分开做，显然是存在无用功。
   • 逆向思维
     如果我们已知总和最大区间的左边界，只需要寻找右边界，很容易通过一次扫描完成。

1.3 思考题

Q1. 将例题1.3的线性复杂度算法写成伪代码。（难度系数2颗星）

如下

sum = 0
max = array[0]
for i = 1 to len
	if sum <= 0 
		sum = -∞
	else if sum = -∞ and array[i] > 0
	    sum = array[i]
	else
	    sum += array[i]
	if max < sum
		max = sum
1
2
3
4
5
6
7
8
9
10
11

Q2．在一个数组中寻找一个区间，使得区间内的数字之和等于某个事先给定的数字。

考虑从左往右滑动窗口（l,r）搜索求和，先动窗口右边（往右），一旦超过给定数字就动左边（往右）。若动到左等于右（sum=0），再动窗口右边。

sum = array[0]
l = 0
for r = 1 to len
	sum += array[r]
	if sum > target
		while sum > target
			sum -= array[l]
			l += 1
	if sum == target
		break
1
2
3
4
5
6
7
8
9
10

Q3. 在一个二维矩阵中，寻找一个矩形的区域，使其中的数字之和达到最大值。

问题从一维变成了二维，但实质是一样的，同样是再求最大子序和，只要将二维转化为一维。
转化的方法可以是对于矩阵的每一列，我们将其加在一起，成为了一维上的一个数，二维矩阵的和转化为了一维数组的和。
参考leetcode题解，引用B站up zjutsunny老师的ppt

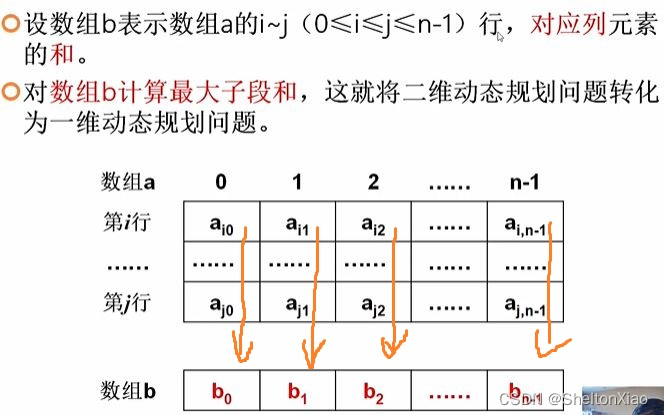
对每i->j行，都可以把二维问题转化为一维问题。

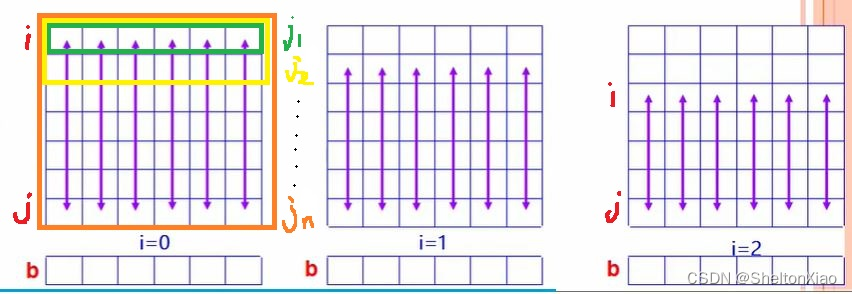
1.4 延伸

最大子序列和还有动态规划求解方法。

参考阅读

1. 吴军-计算之魂
2. leetcode最大子序和
3. 六种姿势拿下连续子序列最大和问题