-
高数_第3章重积分_三重积分的奇偶性
当积分区域 Ω 关于坐标面对称, 被积函数 f(x, y, z) 具有奇偶性时, 利用这些特点可以简化三重积分的计算, 这样的简算也称为对称奇偶性。
一. 假设 Ω 关于Oxy平面对称, Oxy平面将 Ω 对称地分为
 和
和 两部分。
两部分。(1)如果f(x, y, z) 关于z是奇函数, 即总存在 f(x, y, -z) = -f(x, y, z)
则

(2) 如果 f(x, y, z)关于z是偶函数, 即总存在 f(x, y, -z) = f(x, y, z), 则

二. 假设 Ω 关于Oxz平面对称, Oxz平面将 Ω 对称地分为
 和
和  两部分。
两部分。(1)如果f(x, y, z) 关于y是奇函数, 即总存在 f(x, -y, z) = -f(x, y, z)
则

(2) 如果 f(x, y, z)关于y是偶函数, 即总存在 f(x, -y, z) = f(x, y, z), 则

三. 假设 Ω 关于Oyz平面对称, Oxz平面将 Ω 对称地分为
 和
和 两部分。
两部分。 (1)如果f(x, y, z) 关于x是奇函数, 即总存在 f(-x, y, z) = -f(x, y, z)
则

(2) 如果 f(x, y, z)关于 x 是偶函数, 即总存在 f(-x, y, z) = f(x, y, z), 则
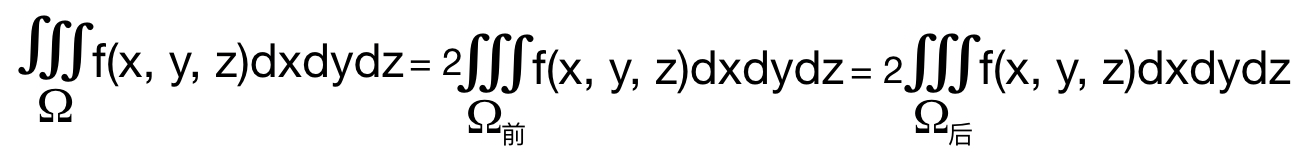
四. 结论: 在重积分中,讨论被积函数f 的奇偶性,不是看函数 f是否关于直角坐标的原点
(或y轴)对称, 这不是我们分析的方向 。 绝不能用一元函数判断奇偶性的老方法!!正确方法:
1 先判断积分区域 关于哪个坐标面对称,
2 然后再将f中的x 代替为-x, 或者是y代替为-y, 或者是z 代替为-z.
3. 再看f(-x, y, z) 或者f(x, -y, z) 或者f(x, y, -z)与哪个函数相等。
简要地说: 先看积分区域, 再将变量替换为相反值, 再看结果。
三重积分的奇偶性判断, 我们必须理解, 必须掌握!
看几个例题
例1:简算三重积分

解: 积分区域 Ω 是一个旋转抛物面,关于yOz坐标面对称, 因此可以判断 被积函数的奇偶性,
被积函数 f(x, y, z) = zsinxsiny² 关于变量x是奇函数. f(-x, y, z) = -f(x, y, z). 所以原积分
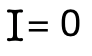
-
相关阅读:
企业架构LNMP学习笔记13
C语言练习8(巩固提升)
Typescript高级: 深入理解extends keyof语法
Springboot整合缓存
算法:记忆化搜索
【随笔】致19期的小伙伴们
手把手教你做测开:开发Web平台之图书新增
【Linux】管道命令split、awk、sed【二】
HTML基础用法
结合RF与1DCNN的多信息融合气温预报方法
- 原文地址:https://blog.csdn.net/ximanni18/article/details/126543781