-
26、Nerfies:Deformable Neural Radiance Fields
简介
主页:https://nerfies.github.io/

DNerf建模了场景内容的变形,但其目的不是为了提供多视角的动态图,而是为了对场景内容发生微小扰动更鲁棒。方法针对的是人的自拍图像,通过前后景分割,获得多张无背景的自拍人像。背景的信息用于相机标定,估计相机姿态参数和内参。在光线追踪过程中,为每一帧事先编码好变形特征,利用特征估计每个点的形变位移,通过位移获取标准空间中的位置,来估计颜色和密度。同样为每一帧准备了外观特征向量,用于处理各帧之间的差异性。Loss中除了重建误差还包括变形的弹性正则项,防止过拟合。类似于Nerf,该方法对空间坐标进行了三角函数编码,转换为更高维的向量。但空间编码在训练过程中被设定为从低频到高频的coarse2fine过程,在防止过拟合的同时不断增加清晰度。创新点
- NeRF的扩展,以处理非刚性变形的物体,优化每次观测的变形场
- 适合神经网络定义的变形场的刚度先验
- 一种从粗到细的正则化方法,在优化过程中调节变形场建模高频的能力
- 一个从随意的手机抓拍重构自由视角自拍的系统。
实现流程
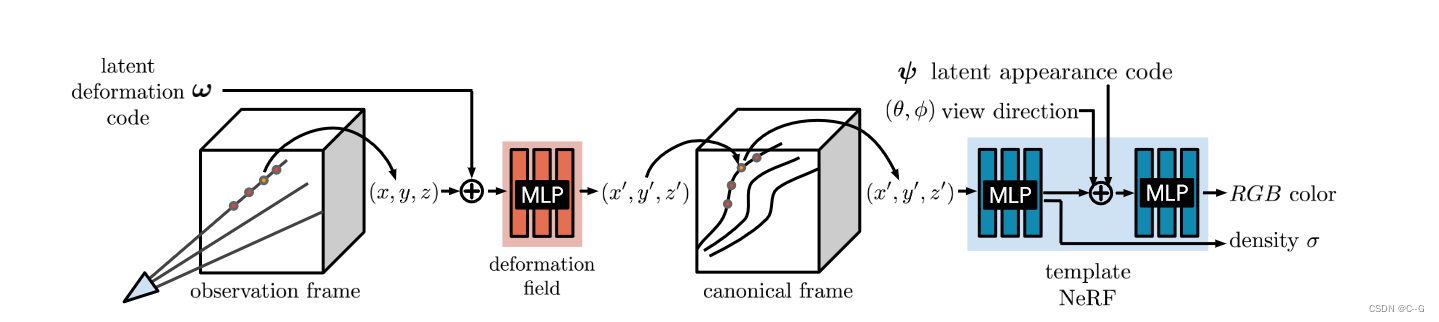
将一个潜在变形码(ω)和一个外观码(ψ)关联到每个图像。在观察框中跟踪摄像机射线,并使用变形场编码为基于变形码ω的MLP,沿着射线将样本变换到标准框。使用转换后的样本(x ', y ', z ')、观察方向(θ, φ)和外观码ψ作为MLP的输入来查询模板NeRF,并沿着NeRF之后的射线对样本进行积分。- 变形网络
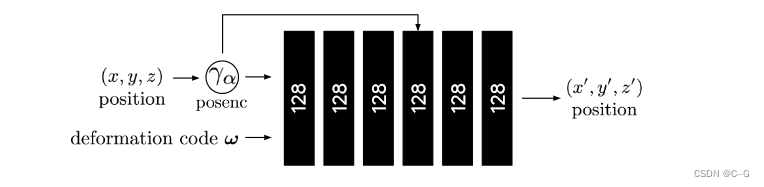 变形网络采用由α参数化的粗到细退火的位置编码位置γα(x),以及变形码ω,输出变形位置x ’
变形网络采用由α参数化的粗到细退火的位置编码位置γα(x),以及变形码ω,输出变形位置x ’- 模板NeRF
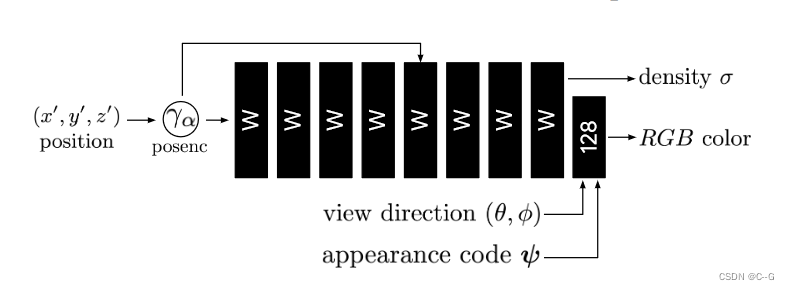
模板NeRF网络与原始的NeRF MLP相同,除了提供了外观潜在代码ψ和视图方向,以允许在模型中调制外观
Neural Radiance Fields
NeRF模板实现紧跟原始的,只是论文使用了Softplus激活ln(1 + ex)作为密度。使用深度为6,隐藏尺寸为128的变形网络,在第四层采用跳跃连接。使用256个粗和细射线样本的全高清模型(1920×1080)和一半的一半分辨率的模型。使用8维的潜在变形和外观码。神经辐射场(NeRF)是一个连续的、体积的表示。它是一个函数F:(x, d, ψi)→(c, σ),将三维位置x = (x, y, z)和观察方向d = (φ, θ)映射为颜色c = (r, g, b)和密度σ。
在实践中,NeRF使用正弦位置编码γ: R3→R3+6m映射输入x和d,定义为γ(x) = (x,···,sin (2kπx), cos (2kπx),···),其中m是控制频带总数的超参数,并且k∈{0,…, m−1},这个函数使用一组频率递增的正弦函数和余弦函数将坐标向量x∈R3投影到高维空间。这使得MLP可以在低频域对高频信号进行建模
与NeRF-W相似,也为每个观察到的帧i∈ {1, . . . , n} 提供了一个外观潜在码ψi,调节颜色输出以处理输入帧之间的外观变化,例如曝光和白平衡
Neural Deformation Fields

NeRF训练程序依赖于这样一个事实:给定一个3D场景,来自两个不同摄像机的两条相交射线应该产生相同的颜色。如果不考虑镜面反射和透射,这个假设对所有静态场景都成立,但是许多场景不是完全静态的
为此扩展了NeRF,以允许重建非刚性变形场景
使用NeRF作为场景的规范模板 使用MLP对其建模连续函数。对每一个坐标系i∈{1,…, n},其中n为观测到的帧数。定义一个映射Ti: x→x ',它将所有观察空间坐标x映射到标准空间坐标x '。使用映射T: (x, ωi)→x '来模拟所有时间步的变形场,该映射以每帧学习的潜在变形码ωi为条件。每个潜在码对帧i中的场景状态进行编码。给定一个正则空间辐射场F和一个观测到正则映射T,可以计算出观测空间辐射场:
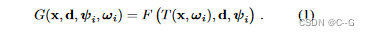
在观测框中投射光线和采样点,然后利用变形场将采样点映射到模板上一个简单的变形模型是位移场V:(x, ωi)→t,定义变换为t (x, ωi) = x + V (x, ωi)。这个公式足以表示所有连续变形;然而,旋转带有平移场的一组点需要对每个点进行不同的平移。因此,用密集的SE(3)场W: (x, ωi)→SE(3)来表示变形。SE(3)变换编码刚体运动,允许用相同的参数旋转一组距离较远的点。
将刚性变换编码为螺旋轴S = (r;v)∈R^6。r∈so(3)编码了一个旋转,其中ˆr = r/‖r‖为旋转轴,θ =‖r‖为旋转角度。r的指数得到一个旋转矩阵e^r∈SO(3)
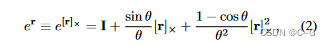
[x]×表示向量x的叉乘矩阵螺旋运动S编码的平移可以恢复为p = Gv
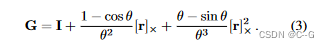
结合这些公式并使用指数映射,得到变换后的点为x ’ = e^S x = e^r x + p。Elastic Regularization
变形场增加了模糊性,导致了约束不足的优化问题,产生了不可信的结果和伪影。例如,一个向后移动的物体在视觉上相当于它在缩小大小。因此,引入先验来引出更可信的解决方案
在几何处理和物理模拟中,通常使用弹性能测量刚体运动对局部变形的偏差来建模非刚体变形,在视觉领域,这些能量被广泛用于非刚性场景和物体的重建和跟踪
Elastic Energy
对于一个固定的潜码ωi,形变场T是一个从R3中的观测坐标到R3中的正则坐标的非线性映射。这个映射在x∈R3点的雅可比矩阵JT (x)描述了该点上变换的最佳线性逼近。因此,我们可以通过JT控制变形的局部行为。与其他使用离散曲面的方法不同,论文的连续公式允许通过MLP的自动微分直接计算JT。有几种方法来惩罚雅可比矩阵JT对刚性变换的偏差。考虑到雅可比矩阵JT = UΣV^T的奇异值分解,多种方法将离最近旋转的偏差惩罚为 ‖JT−R‖^2 f,其中R = VU^T,‖·‖F为Frobenius范数。选择直接使用JT的奇异值,并测量其偏离恒等式。奇异值的对数对同一因子的收缩和展开给予同等的权重,因此,惩罚了对数奇异值从零的偏差:
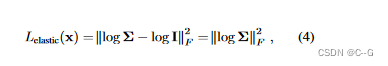
log 是 矩阵的对数Robustness:

虽然人类大多是僵硬的,但有一些动作可以打破对局部僵硬的假设,例如,面部表情会局部拉伸和压缩我们的皮肤。因此,使用鲁棒损失重新映射上述定义的弹性能量
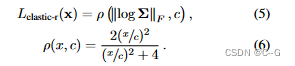
ρ(·)为根据Bar-ron用超参数c = 0.03参数化的Geman-McClure鲁棒误差函数,鲁棒的误差函数使得损失的梯度在参数值较大时降为零,从而减少了训练过程中异常值的影响Weighting:
允许变形场在空白空间中自由活动,因为相对于背景移动的主体需要空间中某处的非刚性变形。因此,根据光线对渲染视图的贡献来权衡每个样本的弹性惩罚
Background Regularization
添加一个正则化项来阻止背景移动,例如:使用来自运动的结构的相机配准产生一组3D特征点,这些点至少在一些观测值上表现严格。给定这些静态的3D点{x1…, xK},我们对运动的惩罚为
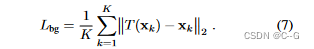
除了保持背景点不移动之外,这种正则化还具有将观测坐标系对准正则坐标系的优点。Coarse-to-Fine Deformation Regularization

在配准和流估计过程中出现的一个常见权衡是在建模微小运动和大型运动之间进行选择,这可能会导致过度平滑的结果或不正确的配准(局部最小值)。使用一个从粗到细的正则化来缓解他们。
在本实现流程开始的Neural Radiance Fields中,提到了位置编码使用超参数m,其控制编码中使用的频带数,它控制了网络的平滑度:m的值越低,就会产生低频偏差(低分辨率),而m的值越大,就会产生高频偏差(高分辨率)
在上图中,由于变形场的m值较小,模型无法捕捉微笑的微小运动;相反,当m较大时,模型不能正确旋转头部,因为模板过度拟合到一个未优化的变形场。为此,论文提出从低频偏差开始到高频偏差结束的粗到细的方法
位置编码可以用NeRF的MLP的神经切线核(NTK)来解释:一个平稳的插值核,其中m控制该核的可调“带宽”。少量的频率会导致一个大的核,导致数据欠拟合,而大量的频率会导致一个窄的核,导致过拟合
通过引入一个参数α来平滑退火NTK的带宽,该参数α窗口的位置编码的频带,类似于如何粗到细的优化方案解决粗解,随后在更高的分辨率细化。
定义每个频带j的权值为
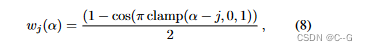
参数α∈[0,m]的线性退火可以理解为在频带内滑动截断的汉恩窗(其中左侧被夹紧到1,右侧被夹紧到0)训练时设置α(t) = mt / N,其中t是当前的训练迭代,N是α应该达到最大频率m时的超参数
Casual Free-Viewpoint Selfies
以一组自拍照片或自拍视频作为输入,在这些照片或视频中,用户基本是站着不动的,即假设主题站在一个静态背景,以使相机的一致几何配准
-
Camera Registration
寻求相机与静态背景的注册。使用COLMAP来计算每个图像和相机内部的姿态。这一步假设后台有足够的特征来注册序列 -
Foreground Segmentation
在某些情况下,SfM会匹配运动主题的特征,导致背景严重错位。这在相关帧的视频捕捉中是有问题的。在这种情况下,它有助于丢弃图像特征的主题,可以使用前景分割网络检测
效果

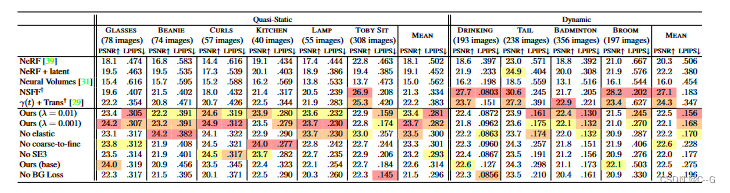
-
相关阅读:
【跟晓月学数据库】基于book库的mysql进阶实战
贪心算法解决雷达站建站问题
十秒看懂computed和watch的区别 (vue的简单计算和复杂监听)
利用随机森林对特征重要性进行评估(公式原理)
成都瀚网科技有限公司:开抖音店铺有哪些注意事项?
初识网页与浏览器
分享几招教会你怎么给图片加边框
流式DMA映射实践3:dmaengine与memcpy
结构型模式总结
编译和连接
- 原文地址:https://blog.csdn.net/weixin_50973728/article/details/126542258