目录

1 VRP中的对称性问题

2 第二个例子

---

本文总结至运小筹公众号某学习群，版权归原作者，如有侵权请联系删除！

1 VRP中的对称性问题

比如考虑一个有3辆车的VRP问题，3辆车都是同质的，具有相同的容量。
假设一个解是
route1 = [0, 1, 3, 4, 5, 0]
route2 = [0, 2, 6, 7, 0]
route3 = [0, 8, 9, 0]

那么，这个解实际上和
route1 = [0, 2, 6, 7, 0]
route2 = [0, 8, 9, 0]
route3 = [0, 1, 3, 4, 5, 0] 

以及

route1 =[0, 8, 9, 0]
route2 =  [0, 2, 6, 7, 0]
route3 = [0, 1, 3, 4, 5, 0] 

这三个解实质上是一模一样的。但是对于求解器来讲，他并不知道这是一样的，他会认为是3个不同的解。但是这样的解有很多，就会对求解模型带来很多冗余的计算。消除对称性就可以在一定程度上加速求解。

那么如何区分这三辆车呢？在VRP语境下，为了破除对称性，我们可以强制约束，第一辆车的载重 >= 第2辆车的载重 >= 第3辆车的载重。即：加入约束

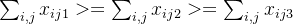
2 第二个例子

例子来源:SYMMETRY IN INTEGER PROGRAMMING

数字案例：

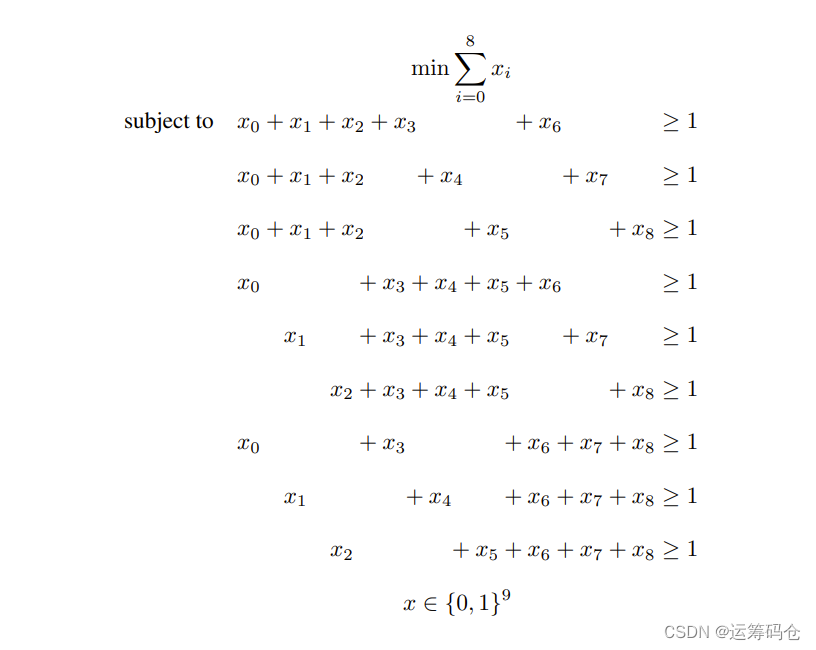
案例分析

打眼一看可能发现不了什么猫腻，但是，我们对这个系数矩阵进行简单分块

 可以发现：

• 如果我们将约束(4)~(6)中
  • 紫色块中的变量x6,x7,x8换成x3,x4和x5，
  • 将红色块中的x3,x4和x5换成x6,x7,x8
  • 我们可以将约束(4)~(6)变换成约束(7)~(9)
  • 并且变换的模型与原模型是等价的

所以，在这个例子中，

• 变量组 (x3,x4,x5) 和 变量组 (x6,x7,x8) 是对称变量。
• 变量组 (x1,x2,x3) 和 变量组 (x6,x7,x8) 是对称变量
• 变量组 (x1,x2,x3) 和 变量组 (x3,x4,x5) 是对称变量