深度了解特征工程

深度了解特征工程
一特征工程介绍（Feature Engineering）

什么是特征工程？特征工程解决了什么问题？为什么特征工程对机器学习很重要？怎么做特征工程？怎么做好特征工程？集众多博友智慧，一文全面了解并应用特征工程。

1 定义及意义

（1）定义
- 特征工程（Feature Engineering）特征工程是将原始数据转化成更好的表达问题本质的特征的过程，使得将这些特征运用到预测模型中能提高对不可见数据的模型预测精度。
- 特征工程简单讲就是发现对因变量y有明显影响作用的特征，通常称自变量x为特征，特征工程的目的是发现重要特征。
- 如何能够分解和聚合原始数据，以更好的表达问题的本质？这是做特征工程的目的。 “feature engineering is manually designing what the input x’s should be.” “you have to turn your inputs into things the algorithm can understand.”
- 特征工程是数据挖掘模型开发中最耗时、最重要的一步。
（2）意义
- 特征工程是一个包含内容很多的主题，也被认为是成功应用机器学习的一个很重要的环节。如何充分利用数据进行预测建模就是特征工程要解决的问题！ “实际上，所有机器学习算法的成功取决于如何呈现数据。” “特征工程是一个看起来不值得在任何论文或者书籍中被探讨的一个主题。但是他却对机器学习的成功与否起着至关重要的作用。机器学习算法很多都是由于建立一个学习器能够理解的工程化特征而获得成功的。”——ScottLocklin，in “Neglected machine learning ideas”
- 数据中的特征对预测的模型和获得的结果有着直接的影响。可以这样认为，特征选择和准备越好，获得的结果也就越好。这是正确的，但也存在误导。预测的结果其实取决于许多相关的属性：比如说能获得的数据、准备好的特征以及模型的选择。
（3）相关概念

Feature：An attribute useful for your modeling task. Feature Selection：From many features to a few that are useful Feature Extraction：The automatic construction of new features from raw data. Feature Construction：The manual construction of new features from raw data. Feature Importance：An estimate of the usefulness of a feature.

1）特征与属性的区别？

并不是所有的属性都可以看做特征，区分它们的关键在于看这个属性对解决这个问题有没有影响！可以认为特征是对于建模任务有用的属性。表格式的数据是用行来表示一个实例，列来表示属性和变量。每一个属性可以是一个特征。特征与属性的不同之处在于，特征可以表达更多的跟问题上下文有关的内容。特征是一个对于问题建模有意义的属性。我们使用有意义（有用的）来区别特征和属性，认为如果一个特征没有意义是不会被认为是特征的，如果一个特征对问题没有影响，那就不是这个问题的一部分。在计算机视觉领域，一幅图像是一个对象，但是一个特征可能是图像中的一行；在自然语言处理中每一个文档或者一条微博是一个对象，一个短语或者单词的计数可以作为特征；在语音识别中，一段声音是一个实例，一个特征可能是单个词或者发音。

2）什么是特征重要性？

特征重要性，可以被认为是一个选择特征重要的评价方法。特征可以被分配一个分值，然后按照这个分值排序，那些具有较高得分的特征可以被选出来包含在训练集中，同时剩余的就可以被忽略。特征重要性得分可以帮助我们抽取或者构建新的特征。挑选那些相似但是不同的特征作为有用的特征。如果一个特征与因变量（被预测的事物）高度相关，那么这个特征可能很重要。相关系数和其他单变量的方法（每一个变量被认为是相互独立的）是比较通用的评估方法。更复杂的方法是通过预测模型算法来对特征进行评分。这些预测模型内部有这样的特征选择机制，比如MARS，随机森林，梯度提升机。这些模型也可以得出变量的重要性。

2 流程及方法

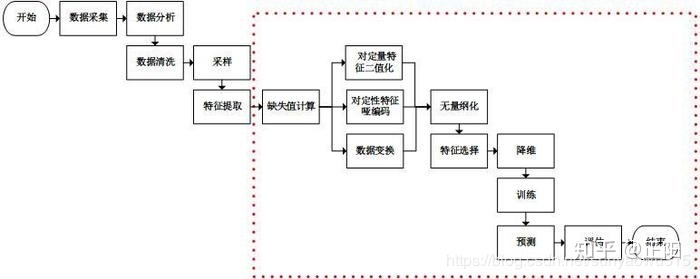
特征工程的定义形形色色，笔者同样对特征工程的全流程有着自己的理解。下面三幅图是比较常见的特征工程流程，可以参考，便于理解。跟深入了解特征工程，还是需要在广泛学习的基础上对其有充分的自我理解。 - 1.图一是基本的数据挖掘场景

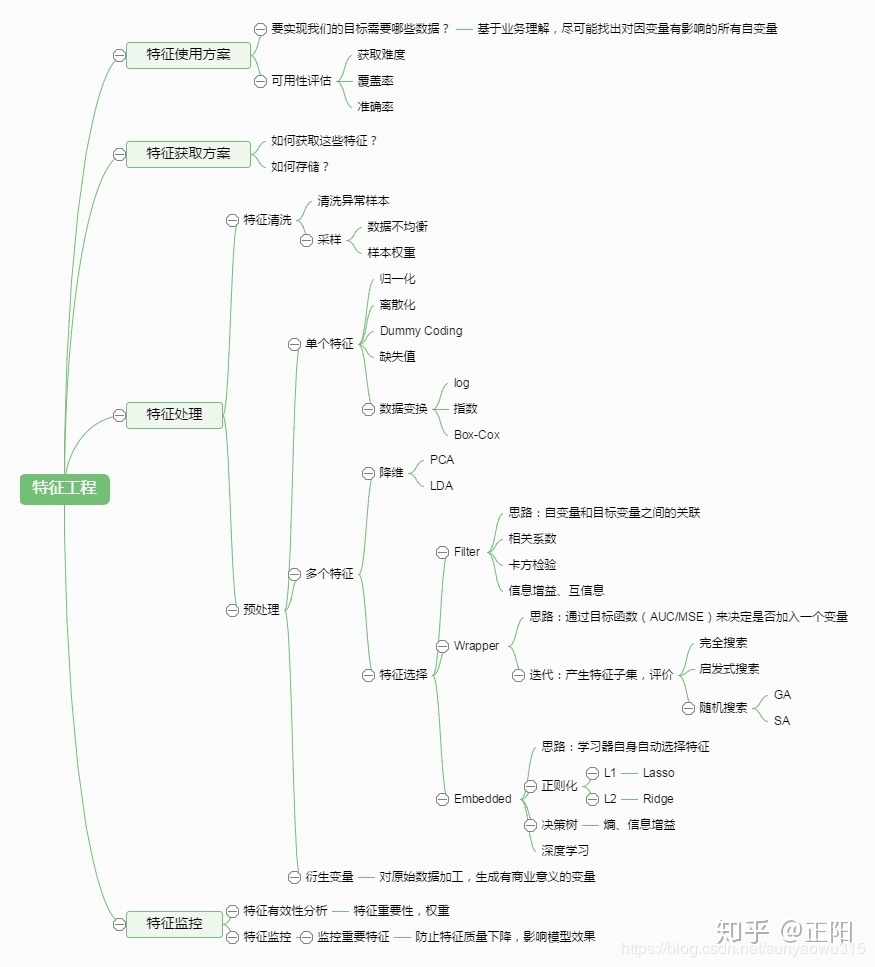
- 2.图二是特征工程的迭代过程

- 3.图三是特征工程的常见方法和步骤

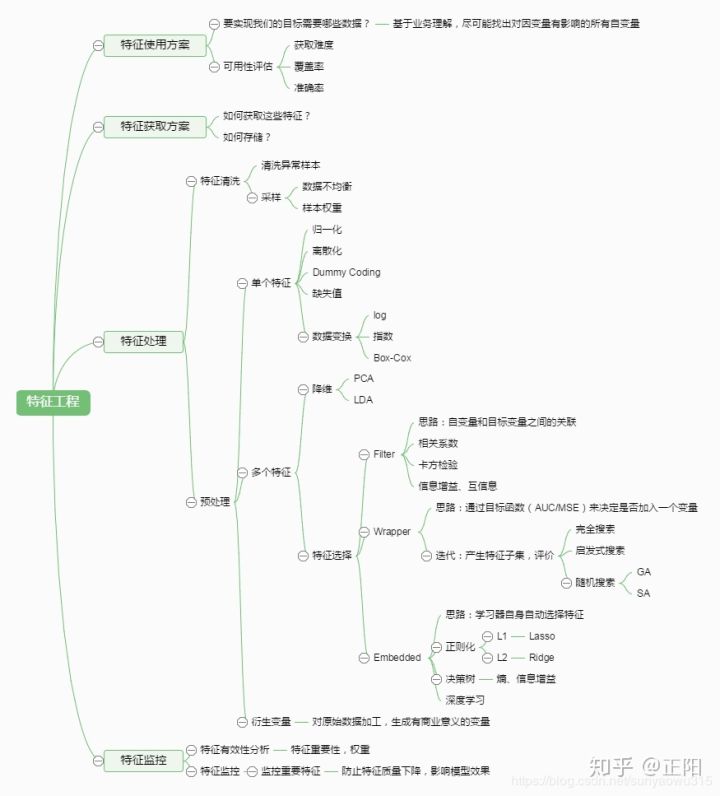
二数据获取

要实现特征工程目标，要用到什么数据？需要结合特定业务，具体情况具体分析。重点考虑如下三方面： ①数据获取途径 - 如何获取特征（接口调用or自己清洗or/github资源下载等） - 如何存储？（/data/csv/txt/array/Dataframe//其他常用分布式）

②数据可用性评估 - 获取难度 - 覆盖率 - 准确率

③特征维度

三数据描述（Feature Describe）

通过数据获取，我们得到未经处理的特征，这时的特征可能有以下问题： - 存在缺失值：缺失值需要补充。 - 不属于同一量纲：即特征的规格不一样，不能够放在一起比较。 - 信息冗余：对于某些定量特征，其包含的有效信息为区间划分，例如学习成绩，假若只关心“及格”或不“及格”，那么需要将定量的考分，转换成“1”和“0”表示及格和未及格。 - 定性特征不能直接使用：某些机器学习算法和模型只能接受定量特征的输入，那么需要将定性特征转换为定量特征。 - 信息利用率低：不同的机器学习算法和模型对数据中信息的利用是不同的。

那么最好先对数据的整体情况做一个描述、统计、分析，并且可以尝试相关的可视化操作。主要可分为以下几方面：

1 数据结构

2 质量检验

标准性、唯一性、有效性、正确性、一致性、缺失值、异常值、重复值

3 分布情况

统计值

包括max, min, mean, std等。python中用pandas库序列化数据后，可以得到数据的统计值。

探索性数据分析（EDA，Exploratory Data Analysis）

集中趋势、离中趋势、分布形状

四特征处理（Feature Processing）

对数据的整体性有一个宏观的了解之后，即需要进入特征工程第一个重要的环节——特征处理，特征处理会消耗大量时间，并且直接影响特征选择的结果。特征处理主要包括： ①数据预处理。即数据的清洗工作，主要为缺失值、异常值、错误值、数据格式、采样度等问题的处理。 ②特征转换。即连续变量、离散变量、时间序列等的转换，便于入模。

1 数据预处理

【特征工程】python特征预处理大全

（1）缺失值处理

有些特征可能因为无法采样或者没有观测值而缺失.例如距离特征，用户可能禁止获取地理位置或者获取地理位置失败，此时需要对这些特征做特殊的处理，赋予一个缺失值。我们在进行模型训练时，不可避免的会遇到类似缺失值的情况，下面整理了几种填充空值的方法

1）缺失值删除（dropna）

①删除实例

②删除特征

2）缺失值填充（fillna）

①用固定值填充

对于特征值缺失的一种常见的方法就是可以用固定值来填充，例如0，9999， -9999, 例如下面对灰度分这个特征缺失值全部填充为-99
```
data['灰度分'] = data['灰度分'].fillna('-99')
```
②用均值填充

对于数值型的特征，其缺失值也可以用未缺失数据的均值填充，下面对灰度分这个特征缺失值进行均值填充
```
data['灰度分'] = data['灰度分'].fillna(data['灰度分'].mean()))
```
③用众数填充

与均值类似，可以用未缺失数据的众数来填充缺失值
```
data['灰度分'] = data['灰度分'].fillna(data['灰度分'].mode()))
```
④用上下数据进行填充
- 用前一个数据进行填充
```
data['灰度分'] = data['灰度分'].fillna(method='pad')
```
- 用后一个数据进行填充
```
data['灰度分'] = data['灰度分'].fillna(method='bfill')
```
⑤用插值法填充
```
data['灰度分'] = data['灰度分'].interpolate()
```
⑥用KNN进行填充
```
from fancyimpute import BiScaler, KNN, NuclearNormMinimization, SoftImpute
dataset = KNN(k=3).complete(dataset)
```
⑦random forest进行填充
```
from sklearn.ensemble import RandomForestRegressor
zero_columns_2 = ['机构查询数量', '直接联系人数量', '直接联系人在黑名单数量', '间接联系人在黑名单数量',
                '引起黑名单的直接联系人数量', '引起黑名单的直接联系人占比']
#将出现空值的除了预测的列全部取出来，不用于训练                
dataset_list2 = [x for x in dataset if x not in zero_columns_2]
dataset_2 = dataset[dataset_list2]
# 取出灰度分不为空的全部样本进行训练
know = dataset_2[dataset_2['灰度分'].notnull()]
print(know.shape) #26417, 54
# 取出灰度分为空的样本用于填充空值
unknow = dataset_2[dataset_2['灰度分'].isnull()]
print(unknow.shape) #2078, 54
y = ['灰度分']
x = [1]
know_x2 = know.copy()
know_y2 = know.copy()
print(know_y2.shape)
#
know_x2.drop(know_x2.columns[x], axis=1, inplace=True)
print(know_y2.shape)
print(know_x2.shape)
#
know_y2 = know[y]
# RandomForestRegressor
rfr = RandomForestRegressor(random_state=666, n_estimators=2000, n_jobs=-1)
rfr.fit(know_x2, know_y2)
# 填充为空的样本
unknow_x2 = unknow.copy()
unknow_x2.drop(unknow_x2.columns[x], axis=1, inplace=True)
print(unknow_x2.shape) #(2078, 53)
unknow_y2 = rfr.predict(unknow_x2)
unknow_y2 = pd.DataFrame(unknow_y2, columns=['灰度分'])
```
⑧使用fancyimpute包中的其他方法
```
# matrix completion using convex optimization to find low-rank solution
# that still matches observed values. Slow!
X_filled_nnm = NuclearNormMinimization().complete(X_incomplete)
# Instead of solving the nuclear norm objective directly, instead
# induce sparsity using singular value thresholding
X_filled_softimpute = SoftImpute().complete(X_incomplete_normalized)
# print mean squared error for the three imputation methods above
nnm_mse = ((X_filled_nnm[missing_mask] - X[missing_mask]) ** 2).mean()
# print mean squared error for the three imputation methods above
nnm_mse = ((X_filled_nnm[missing_mask] - X[missing_mask]) ** 2).mean()
print("Nuclear norm minimization MSE: %f" % nnm_mse)
softImpute_mse = ((X_filled_softimpute[missing_mask] - X[missing_mask]) ** 2).mean()
print("SoftImpute MSE: %f" % softImpute_mse)
knn_mse = ((X_filled_knn[missing_mask] - X[missing_mask]) ** 2).mean()
print("knnImpute MSE: %f" % knn_mse)
```
⑨缺失值作为数据的一部分不填充

LightGBM和XGBoost都能将NaN作为数据的一部分进行学习，所以不需要处理缺失值。

（2）异常值处理

1）特征异常平滑
- 基于统计的异常点检测算法例如极差，四分位数间距，均差，标准差等，这种方法适合于挖掘单变量的数值型数据。
- 基于距离的异常点检测算法主要通过距离方法来检测异常点，将数据集中与大多数点之间距离大于某个阈值的点视为异常点，主要使用的距离度量方法有绝对距离(曼哈顿距离)、欧氏距离和马氏距离等方法。
- 基于密度的异常点检测算法考察当前点周围密度，可以发现局部异常点。
（3）重复值处理

根据需求判断是否需要去重操作

（4）数据格式处理
- 数字类型的转换
- 数字单位的调整
- 时间格式的处理
（5）数据采样

多的类别过采样/少的类别欠采样来平衡分布欠采样（undersampling）和过采样（oversampling）会对模型带来不一样的影响。

2 特征转换

特征也就是我们常常说的变量/自变量，一般分为三类： - 连续型 - 无序类别（离散）型 - 有序类别（离散）型

主要转换方式有以下几种：

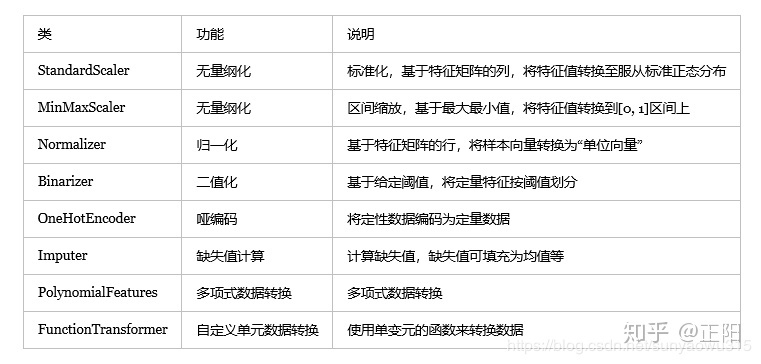
（1）连续型特征处理

1）函数转换

有时我们的模型的假设条件是要求自变量或因变量服从某特殊分布（如正太分布），或者说自变量或因变量服从该分布时，模型的表现较好。这个时候我们就需要对特征或因变量进行非线性函数转换。这个方法操作起来很简单，但记得对新加入的特征做归一化。对于特征的转换，需要将转换之后的特征和原特征一起加入训练模型进行训练。

2）特征缩放

某些特征比其他特征具有较大的跨度值。举个例子，将一个人的收入和他的年龄进行比较，更具体的例子，如某些模型（像岭回归）要求你必须将特征值缩放到相同的范围值内。通过缩放可以避免某些特征比其他特征获得大小非常悬殊的权重值。

3）无量纲化

无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化、归一化、区间缩放法。标准化的前提是特征值服从正态分布，标准化后，其转换成标准正态分布。区间缩放法利用了边界值信息，将特征的取值区间缩放到某个特点的范围，例如[0, 1]等。把数据放缩到同样的范围 SVM/NN影响很大树模型影响小。不是什么时候都需要标准化，比如物理意义非常明确的经纬度，如果标准化，其本身的意义就会丢失。

①标准化

· 均值方差法

· z-score标准化

· StandardScaler标准化

标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。标准化需要计算特征的均值和标准差，公式表达为：

使用preproccessing库的StandardScaler类对数据进行标准化的代码如下：
```
from sklearn.preprocessing import StandardScaler
#标准化，返回值为标准化后的数据
StandardScaler().fit_transform(iris.data)
```
②归一化

· 最大最小归一化（最常用）

· 对数函数转换（log）

· 反余切转换

归一化是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”。规则为l2的归一化公式如下：

使用preproccessing库的Normalizer类对数据进行归一化的代码如下：
```
from sklearn.preprocessing import Normalizer
#归一化，返回值为归一化后的数据
Normalizer().fit_transform(iris.data)
```
③区间缩放法

区间缩放法的思路有多种，常见的一种为利用两个最值进行缩放，公式表达为：

使用preproccessing库的MinMaxScaler类对数据进行区间缩放的代码如下：
```
from sklearn.preprocessing import MinMaxScaler
#区间缩放，返回值为缩放到[0, 1]区间的数据
MinMaxScaler().fit_transform(iris.data)
压缩范围
有些分类变量的少部分取值可能占据了90%的case，这种情况下可以采用预测模型、领域专家、或者简单的频率分布统计。具体问题具体分析，高频和低频都是需要特别处理的地方，抛弃效果不好时，可以考虑采样（高频）或上采样（低频），加权等等方法。
```
4）二值化（定量特征）

特征的二值化处理是将数值型数据输出为布尔类型。其核心在于设定一个阈值，当样本书籍大于该阈值时，输出为1，小于等于该阈值时输出为0。我们通常使用preproccessing库的Binarizer类对数据进行二值化处理。定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0，公式表达如下：

使用preproccessing库的Binarizer类对数据进行二值化的代码如下：
```
from sklearn.preprocessing import Binarizer
 #二值化，阈值设置为3，返回值为二值化后的数据
Binarizer(threshold=3).fit_transform(iris.data)
```
5）离散化分箱处理(数值型转类别型)

有时候，将数值型属性转换成类别型更有意义，同时将一定范围内的数值划分成确定的块，使算法减少噪声的干扰。在实际应用中，当你不想让你的模型总是尝试区分值之间是否太近时，分区能够避免过拟合。例如，如果你所感兴趣的是将一个城市作为整体，这时你可以将所有落入该城市的维度值进行整合成一个整体。分箱也能减小错误的影响，通过将一个给定值划入到最近的块中。对于一些特殊的模型（信用评分卡）开发，有时候我们需要对连续型的特征（年龄、收入）进行离散化。常用的离散化方法包括等值划分和等量划分。例如某个特征的取值范围为[0，10]，我们可以将其划分为10段，[0,1),[1,2),⋯,[9,10) - 离散特征的增加和减少都很容易，易于模型的快速迭代； - 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展； - 离散化后的特征对异常数据有很强的鲁棒性模型也会更稳定； - 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性提升表达能力； - 特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险

离散化方法的关键是怎么确定分段中的离散点，下面介绍几种常用的离散化方法： - 等距离离散（等距分组）顾名思义，就是离散点选取等距点。 - 等样本点离散（等深分组）选取的离散点保证落在每段里的样本点数量大致相同 - 决策树离散化（最优分组）决策树离散化方法通常也是每次离散化一个连续特征，原理如下：单独用此特征和目标值y训练一个决策树模型，然后把训练获得的模型内的特征分割点作为离散化的离散点。 - 其他离散化方法其中，最优分组除决策树方法以外，还可以使用卡方分箱的方法，这种方法在评分卡开发中比较常见。

6）不处理

除了归一化（去中心，方差归一），不用做太多特殊处理，可以直接把连续特征扔到模型里使用。根据模型类型而定。

（2）离散型特征处理

1）数值化处理

二分类问题：能够将类别属性转换成一个标量，最有效的场景应该就是二分类的情况。即{0,1}对应{类别1，类别2}。这种情况下，并不需要排序，并且你可以将属性的值理解成属于类别1或类别2的概率。多分类问题：选取多分类，编码到[0，classnum)。类别不平衡问题：样本层面可以采用oversampling/undersampling. 算法层面可以采用代价敏感方法/样本设置权重也不是所有的无序变量都需要做数值化处理，决策树、随机森林等树模型可能不需要处理，视情况而定。

例：label encoder 一个变量的k个值，按序转换成k个数字（1，2，3…k）。例如一个人的状态status有三种取值：bad, normal, good，显然bad < normal < good。这个时候bad, normal, good就可以分别转换成 1、2、3。该方法局限性较大： - 不适用于建立预测具体数值的模型，比如线性回归，只能用于分类， - 即使用于分类，也有一些模型不适合， - 可能结果的精度不如one-hot编码。

2）哑编码

①独热编码(one-hot)

例：再次举一个简单的例子，由{红，绿、蓝}组成的颜色属性，最常用的方式是把每个类别属性转换成二元属性，即从{0,1}取一个值。因此基本上增加的属性等于相应数目的类别。对于数据集中的每个实例，只有一个是1（其他的为0），这也就是独热（one-hot)编码方式（类似于转换成哑变量）。如果你不了解这个编码的话，你可能会觉得分解会增加没必要的麻烦（因为编码大量的增加了数据集的维度）。相反，你可能会尝试将类别属性转换成一个标量值，例如颜色属性可能会用{1,2,3}表示{红，绿，蓝}。这里存在两个问题，首先，对于一个数学模型，这意味着某种意义上红色和绿色比和蓝色更“相似”（因为|1-3| > |1-2|）。除非你的类别拥有排序的属性（比如铁路线上的站），这样可能会误导你的模型。然后，可能会导致统计指标（比如均值）无意义，更糟糕的情况是，会误导你的模型。还是颜色的例子，假如你的数据集包含相同数量的红色和蓝色的实例，但是没有绿色的，那么颜色的均值可能还是得到2，也就是绿色的意思。

哑编码主要是采用N位状态寄存器来对N个状态进行编码，一个变量N个值就转换成N个虚拟变量，每个状态都由他独立的寄存器位，并且在任意时候只有一位有效。使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。在回归，分类，聚类等机器等学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。

优点：简单，且保证无共线性。将离散型特征使用one-hot编码，确实会让特征之间的距离计算更加合理。对离散型特征进行one-hot编码可以加快计算速度。缺点：太稀（稀疏矩阵）避免产生稀疏矩阵的常见方法是降维，将变量值较多的分类维度，尽可能降到最少，能降则降，不能降的，别勉强。

②顺序性哑变量

与one-hot编码一样，都是将一个变量的k个值生成k个哑变量，但同时保护了特征的顺序关系。一般的表达方式如下：

（上面这种表达方式很巧妙地利用递进表达了值之间的顺序关系。）

（3）时间序列处理

1）时间戳处理

时间戳属性通常需要分离成多个维度比如年、月、日、小时、分钟、秒钟。但是在很多的应用中，大量的信息是不需要的。比如在一个监督系统中，尝试利用一个’位置+时间‘的函数预测一个城市的交通故障程度，这个实例中，大部分会受到误导只通过不同的秒数去学习趋势，其实是不合理的。并且维度’年’也不能很好的给模型增加值的变化，我们可能仅仅需要小时、日、月等维度。因此在呈现时间的时候，试着保证你所提供的所有数据是你的模型所需要的。并且别忘了时区，假如你的数据源来自不同的地理数据源，别忘了利用时区将数据标准化。

五特征选择（Feature Selection）

1 特征检验

（1）单变量

1）正态性检验

2）显著性分析

（2）多变量

1）一致性检验

2）多重共线性

2 特征选择

（1）定义

从大量的特征中选择少量的有用特征。不是所有的特征都是平等的。那些与问题不相关的属性需要被删除；还有一些特征可以比其他特征更重要；也有的特征跟其他的特征是冗余的。特征选择就是自动地选择对于问题最重要的特征的一个子集。

（2）作用
- 简化模型，增加模型的可解释性
- 缩短训练时间
- 避免维度灾难
- 改善模型通用性、降低过拟合
（3）方法

判断特征是否发散：如果一个特征不发散，就是说这个特征大家都有或者非常相似，说明这个特征不需要。判断特征和目标是否相关：与目标的相关性越高，越应该优先选择。按照特征评价标准分类：选择使分类器的错误概率最小的特征或者特征组合。利用距离来度量样本之间相似度。利用具有最小不确定性（Shannon熵、Renyi熵和条件熵）的那些特征来分类。利用相关系数, 找出特征和类之间存在的相互关系；利用特征之间的依赖关系, 来表示特征的冗余性加以去除。 - 特征选择算法可以利用得分排序的方法选择特征，如相关性和其他特征重要性手段； - 更高级的方法通过试错来搜索特征子集。这些方法通过建立模型，评价模型，然后自动的获得对于目标最具预测能力的特征子集。 - 还有一些算法能得到特征选择的副产品。比如说逐步回归就是能够自动的选择特征来构建模型。 - 正则化的方法比如lasso和岭回归可以作为特征选择的算法。他们在构建模型的过程中删去或者减小不重要特征的贡献。（An Introduction to feature selection）

根据特征选择的形式可以将特征选择方法分为3种： - Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。 - Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。 - Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。

1）过滤式（Filter）

过滤式特征选择的评价标准从数据集本身的内在性质获得，与特定的学习算法无关，因此具有较好的通用性。通常选择和类别相关度大的特征或者特征子集。过滤式特征选择的研究者认为，相关度较大的特征或者特征子集会在分类器上获得较高的准确率。过滤式特征选择的评价标准分为四种，即距离度量、信息度量、关联度度量以及一致性度量。优点：算法的通用性强；省去了分类器的训练步骤，算法复杂性低，因而适用于大规模数据集；可以快速去除大量不相关的特征，作为特征的预筛选器非常合适。缺点：由于算法的评价标准独立于特定的学习算法，所选的特征子集在分类准确率方面通常低于Wrapper方法。

①方差选择法

使用方差选择法，先要计算各个特征的方差，选择方差大于阈值的特征 (Analysis of Variance：ANOVA,方差分析，通过分析研究不同来源的变异对总变异的贡献大小，从而确定可控因素对研究结果影响力的大小)。
```
from sklearn.feature_selection import VarianceThreshold
#方差选择法，返回值为特征选择后的数据
#参数threshold为方差的阈值
VarianceThreshold(threshold=3).fit_transform(iris.data)
```
②相关系数法

使用相关系数法，先要计算各个特征对目标值的相关系数以及相关系数的P值。用feature_selection库的SelectKBest类结合相关系数来选择特征的代码如下：
```
from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr
#选择K个最好的特征，返回选择特征后的数据
#第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。在此定义为计算相关系数
#参数k为选择的特征个数
SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
```
皮尔逊系数只能衡量线性相关性而互信息系数能够很好地度量各种相关性，但是计算相对复杂一些，好在很多toolkit里边都包含了这个工具（如sklearn的MINE），得到相关性之后就可以排序选择特征了 (皮尔逊相关系数，更多反应两个服从正态分布的随机变量的相关性，取值范围在 [-1,+1] 之间。)

③互信息法

计算各个特征的信息增益 Linear Discriminant Analysis(LDA，线性判别分析)：更像一种特征抽取方式，基本思想是将高维的特征影到最佳鉴别矢量空间，这样就可以抽取分类信息和达到压缩特征空间维数的效果。投影后的样本在子空间有最大可分离性。经典的互信息也是评价定性自变量对定性因变量的相关性的，互信息计算公式如下：

为了处理定量数据，最大信息系数法被提出，使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下：
```
from sklearn.feature_selection import SelectKBest
from minepy import MINE
#由于MINE的设计不是函数式的，定义mic方法将其为函数式的，返回一个二元组，二元组的第2项设置成固定的P值0.5
def mic(x, y):
    m = MINE()
    m.compute_score(x, y)
    return (m.mic(), 0.5)
#选择K个最好的特征，返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
```
④卡方检验（Chi-Square）

就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合。优点：快速，只需要基础统计知识。缺点：特征之间的组合效应难以挖掘。经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量：

这个统计量的含义简而言之就是自变量对因变量的相关性。用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：
```
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2 
#选择K个最好的特征，返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
```
特点：执行时间短（+）：一般不会在数据集上进行迭代计算，且是分类器无关的，相比于训练分类器要快。一般性（+）：评价数据中属性的本身的性质，而不是属性与特定分类器的关联关系（适合程度），所以得到的结果更具有一般性，而且对于很多分类器都能表现“良好”。选择大规模子集（-）：倾向于选择全部最优的特征子集，导致决定停止的条件决定权交给了用户，具有较强的主观性

2）封装式（Wrapper）

Wrapper：封装式特征选择是利用学习算法的性能评价特征子集的优劣。因此，对于一个待评价的特征子集，Wrapper方法需要训练一个分类器，根据分类器的性能对该特征子集进行评价。Wrapper方法中用以评价特征的学习算法是多种多样的，例如决策树、神经网络、贝叶斯分类器、近邻法、支持向量机等等。优点：相对于Filter方法，Wrapper方法找到的特征子集分类性能通常更好。缺点：Wrapper方法选出的特征通用性不强，当改变学习算法时，需要针对该学习算法重新进行特征选择；由于每次对子集的评价都要进行分类器的训练和测试，所以算法计算复杂度很高，尤其对于大规模数据集来说，算法的执行时间很长。

基于目标函数

①完全搜索[穷举]

· 递归特征消除法

递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下：

· 递归特征消除法递归消除法

使用基模型(如LR)在训练中进行迭代，选择不同特征构建单个特征的模型，通过模型的准确性为特征排序，借此来选择特征

②启发式搜索[贪心]

· 前向选择法

从0开始不断向模型加能最大限度提升模型效果的特征数据用以训练，直到任何训练数据都无法提升模型表现。

· 后向剃除法

先用所有特征数据进行建模，再逐一丢弃贡献最低的特征来提升模型效果，直到模型效果收敛。优点：直接面向算法优化，不需要太多知识。缺点：庞大的搜索空间，需要定义启发式策略。
```
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)
```
③随机搜索[策略+好运气]

Wrapper特点：准确性（+）：由于特征子集是针对特定的分类器调准，能获得较好的识别率。泛化能力（+）：有很多机制可以防止过拟合，例如在分类器中可以使用交叉验证等技术。执行速度（-）：对于每个候选的特征子集，必须重新训练一个分类器甚至多个分类器（交叉验证），所以对于计算密集型非常不适合。一般性（-）：由于此种方法对分类器敏感，而不同的分类器具有不同原理的评价函数（损失函数），只能说最终选择特征子集是对当前分类器“最好”的。

3）嵌入式（Embedded）

在嵌入式特征选择中，特征选择算法本身作为组成部分嵌入到学习算法里。最典型的即决策树算法，如ID3、C4.5以及CART算法等，决策树算法在树增长过程的每个递归步都必须选择一个特征，将样本集划分成较小的子集，选择特征的依据通常是划分后子节点的纯度，划分后子节点越纯，则说明划分效果越好，可见决策树生成的过程也就是特征选择的过程。嵌入法Embedded(效果最好速度最快，模式单调，快速并且效果明显，但是如何参数设置，需要深厚的背景知识。) 在模型既定的条件下，寻找最优特征子集 - 正则化项（ L1、L2 ） - LASSO回归 - 岭回归（RidgeRegression） - 决策树 - ID3、C4.5、CART - 深度学习

①基于惩罚项

使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。使用带惩罚项的基模型进行特征选择比如LR加入正则。通过L1正则项来选择特征：L1正则方法具有稀疏解的特性，因此天然具备特征选择的特性，但是要注意，L1没有选到的特征不代表不重要，原因是两个具有高相关性的特征可能只保留了一个，如果要确定哪个特征重要应再通过L2正则方法交叉检验使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型，来选择特征的代码如下：
```
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
#带L1惩罚项的逻辑回归作为基模型的特征选择
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)
```
L1惩罚项降维的原理在于保留多个对目标值具有同等相关性的特征中的一个，所以没选到的特征不代表不重要。故，可结合L2惩罚项来优化。具体操作为：若一个特征在L1中的权值为1，选择在L2中权值差别不大且在L1中权值为0的特征构成同类集合，将这一集合中的特征平分L1中的权值，故需要构建一个新的逻辑回归模型：
```
from sklearn.linear_model import LogisticRegression
 
class LR(LogisticRegression):
    def __init__(self, threshold=0.01, dual=False, tol=1e-4, C=1.0,
                 fit_intercept=True, intercept_scaling=1, class_weight=None,
                 random_state=None, solver='liblinear', max_iter=100,
                 multi_class='ovr', verbose=0, warm_start=False, n_jobs=1):
 
        #权值相近的阈值
        self.threshold = threshold
        LogisticRegression.__init__(self, penalty='l1', dual=dual, tol=tol, C=C,
                 fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight=class_weight,
                 random_state=random_state, solver=solver, max_iter=max_iter,
                 multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs)
        #使用同样的参数创建L2逻辑回归
        self.l2 = LogisticRegression(penalty='l2', dual=dual, tol=tol, C=C, fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight = class_weight, random_state=random_state, solver=solver, max_iter=max_iter, multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs)
 
    def fit(self, X, y, sample_weight=None):
        #训练L1逻辑回归
        super(LR, self).fit(X, y, sample_weight=sample_weight)
        self.coef_old_ = self.coef_.copy()
        #训练L2逻辑回归
        self.l2.fit(X, y, sample_weight=sample_weight)
 
        cntOfRow, cntOfCol = self.coef_.shape
        #权值系数矩阵的行数对应目标值的种类数目
        for i in range(cntOfRow):
            for j in range(cntOfCol):
                coef = self.coef_[i][j]
                #L1逻辑回归的权值系数不为0
                if coef != 0:
                    idx = [j]
                    #对应在L2逻辑回归中的权值系数
                    coef1 = self.l2.coef_[i][j]
                    for k in range(cntOfCol):
                        coef2 = self.l2.coef_[i][k]
                        #在L2逻辑回归中，权值系数之差小于设定的阈值，且在L1中对应的权值为0
                        if abs(coef1-coef2) < self.threshold and j != k and self.coef_[i][k] == 0:
                            idx.append(k)
                    #计算这一类特征的权值系数均值
                    mean = coef / len(idx)
                    self.coef_[i][idx] = mean
        return self
```
使用feature_selection库的SelectFromModel类结合带L1以及L2惩罚项的逻辑回归模型，来选择特征的代码如下：
```
from sklearn.feature_selection import SelectFromModel
#带L1和L2惩罚项的逻辑回归作为基模型的特征选择
#参数threshold为权值系数之差的阈值
SelectFromModel(LR(threshold=0.5, C=0.1)).fit_transform(iris.data, iris.target)
```
②基于树模型

基于树模型的特征选择法树模型中GBDT也可用来作为基模型进行特征选择，使用feature_selection库的SelectFromModel类结合GBDT模型，来选择特征的代码如下：训练能够对特征打分的预选模型：RandomForest和Logistic Regression等都能对模型的特征打分，通过打分获得相关性后再训练最终模型； - Lasso - Elastic Net - Ridge Regression 优点：快速，并且面向算法。缺点：需要调整结构和参数配置，而这需要深入的知识和经验。
```
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
#GBDT作为基模型的特征选择
SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)
```
③深度学习

目前这种手段正在随着深度学习的流行而成为一种手段，尤其是在计算机视觉领域，原因是深度学习具有自动学习特征的能力，这也是深度学习又叫unsupervised feature learning的原因。从深度学习模型中选择某一神经层的特征后就可以用来进行最终目标模型的训练了。在特征学习中，K-means算法可以将一些没有标签的输入数据进行聚类，然后使用每个类别的质心来生成新的特征。

3 特征构造

（1）定义

从原始数据中构造新特征在机器学习或者统计学中，又称为变量选择、属性选择或者变量子集选择，是在模型构建中，选择相关特征并构成特征子集的过程。根据已有特征生成新特征，增加特征的非线性。常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。特征工程中引入的新特征，需要验证它确实能提高预测得准确度，而不是加入一个无用的特征增加算法运算的复杂度。特征重要性和特征选择可以告诉你特征的效用。你需要构造新的特征出来。这要求你在样本数据上花费大量的时间并且思考问题的本质，数据的结构，以及怎么最好的在预测模型中利用他们。

（2）作用

对于表格型数据，通常对特征进行混合聚集，组合或者分解分割来创造新的特征；对于文本数据通常需要设计特定的与问题相关的文档指标；对于图像数据通常需要花费大量时间指示过滤器发现相关的特征。这部分就是人们通常认为的特征工程最具艺术性的部分。这是一个漫长的部分，需要耗费大量的脑力和时间，并可以产生巨大的不同。

（3）方法

1）简单构造

①四则运算

比如原来的特征是x1和x2，那么x1+x2就是一个新的特征，或者当x1大于某个数c的时候，就产生一个新的变量x3，并且x3=1，当x1小于c的时候，x3=0，所以这样看来呢，可以按照这种方法构造出很多特征，这个就是构造。

②特征交叉(组合分类特征)

交叉特征算是特征工程中非常重要的方法之一了，它是将两个或更多的类别属性组合成一个。当组合的特征要比单个特征更好时，这是一项非常有用的技术。数学上来说，是对类别特征的所有可能值进行交叉相乘。假如拥有一个特征A,A有两个可能值{A1，A2}。拥有一个特征B，存在{B1，B2}等可能值。然后，A&B之间的交叉特征如下：{（A1，B1），（A1，B2），（A2，B1），（A2，B2）}，并且你可以给这些组合特征取任何名字，但是需要明白每个组合特征其实代表着A和B各自信息协同作用。一个更好地诠释好的交叉特征的实例是类似于（经度，纬度）。一个相同的经度对应了地图上很多的地方，纬度也是一样。但是一旦你将经度和纬度组合到一起，它们就代表了地理上特定的一块区域，区域中每一部分是拥有着类似的特性。

③分解类别特征

对于一个特征item_color有‘red’、‘green’、‘unknown’三个取值，那么可以创造一些新的特征例如： - 二值特征has_color： 1知道具体颜色，0表示不知道。这个可以替换item_color特征用到更简单的线性模型中。 - 三个二值特征is_red、is_green和is_unknown。这个可以添加到原有特征中用到决策树模型中。

④重构数值量

单位转换整数部分与小数部分分离构造范围二值特征构造阶段性的统计特征构造其他二值特征

⑤分解Datatime

⑥窗口变量统计

2）机器学习

①监督式学习

②非监督式学习

4 特征提取

（1）定义

可能由于特征矩阵过大，一些样本如果直接使用预测模型算法可能在原始数据中有太多的列被建模，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。特征提取是一个自动化的降维过程。使得特征太多的样本被建模的维数降低。

（2）作用

最大限度地降低数据的维度的前提下能够同时保证保留目标的重要的信息，特征提取涉及到从原始属性中自动生成一些新的特征集的一系列算法，降维算法就属于这一类。特征提取是一个自动将观测值降维到一个足够建模的小数据集的过程。数据降维有以下几点好处： 1、避免维度灾难，导致算法失效，或者时间复杂度高 2、避免高维数据中引入的噪声，防止过拟合 3、压缩存储，可视化分析

（3）方法

对于列表数据，可使用的方法包括一些投影方法，像主成分分析和无监督聚类算法。对于图形数据，可能包括一些直线检测和边缘检测，对于不同领域有各自的方法。特征提取的关键点在于这些方法是自动的（只需要从简单方法中设计和构建得到），还能够解决不受控制的高维数据的问题。大部分的情况下，是将这些不同类型数据（如图，语言，视频等）存成数字格式来进行模拟观察。不同的数据降维方法除了实现降维目标的作用，同时具有各自的特点，比如主成分分析，降维后的各个特征在坐标上是正交；非负矩阵分解，因为在一些文本，图像领域数据要求非负性，非负矩阵分解在降维的同时保证降维后的数据均非负；字典学习，可以基于任意基向量表示，特征之间不再是独立，或者非负；局部线性嵌入，是一种典型的流型学习方法，具有在一定邻域保证样本之间的距离不变性。

1）线性降维

常见的降维方法除了基于L1惩罚项的模型以外，另外还有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。

①主成分分析法（PCA）

主成分分析主成分分析算法（PCA）利用主成分分析方法，实现降维和降噪的功能。目前支持稠密数据格式。

选择方差最大的K个特征[无监督] 使用decomposition库的PCA类选择特征的代码如下：
```
from sklearn.decomposition import PCA
#主成分分析法，返回降维后的数据
#参数n_components为主成分数目
PCA(n_components=2).fit_transform(iris.data)
```
【特征工程】PCA原理

②线性判别分析法（LDA）

选择分类性能最好的特征[有监督] 使用lda库的LDA类选择特征的代码如下：
```
from sklearn.lda import LDA
#线性判别分析法，返回降维后的数据
#参数n_components为降维后的维数
 LDA(n_components=2).fit_transform(iris.data, iris.target)
```
③局部线性嵌入/LLE

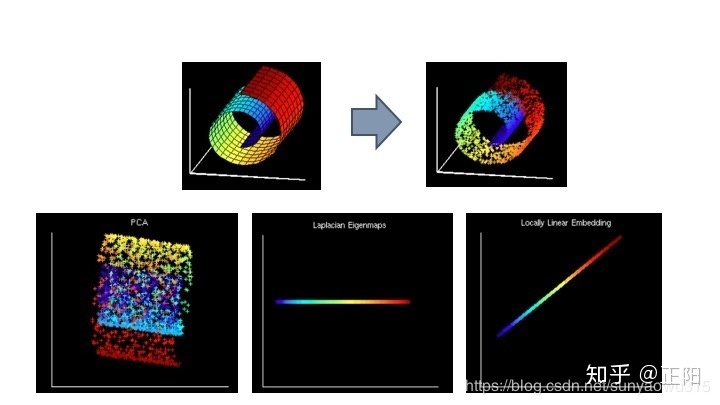
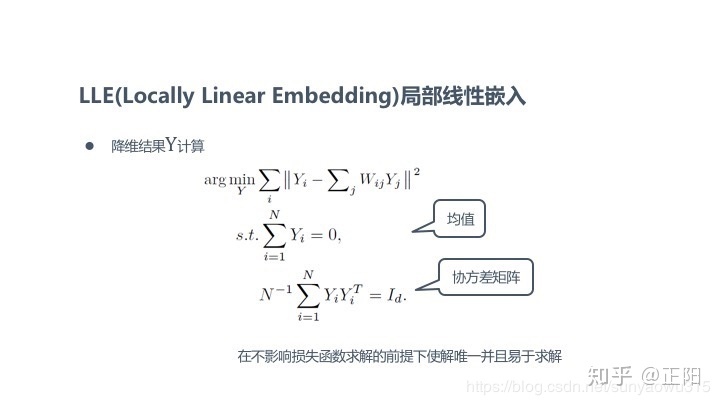
④拉普拉斯特征映射/LE

⑤随机邻域嵌入/SNE

⑥t-分布邻域嵌入/T-SNE

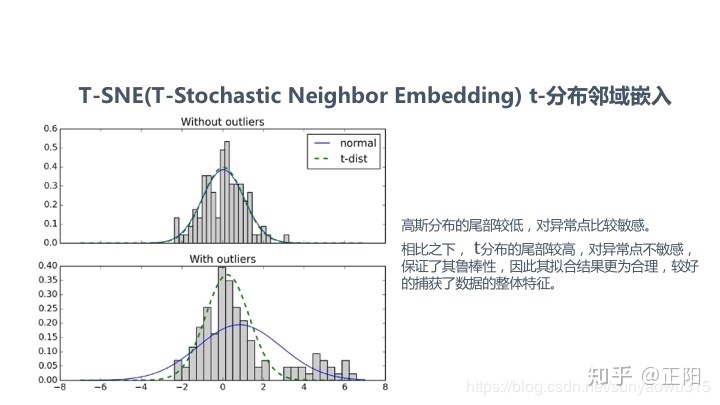
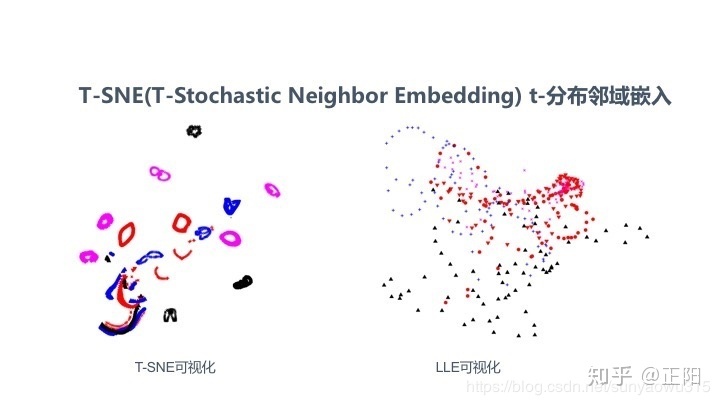
2）非线性降维

①核主成分分析(KPCA):带核函数的PCA

局部线性嵌入(LLE):利用流形结构进行降维还有拉普拉斯图、MDS等

3）迁移学习降维

①迁移成分分析(TCA):不同领域之间迁移学习降维

六入模评估

1 作用

模型评估一般有两个目的： 1. 检验特征工程的工作，查看所选择的特征是否有利于提升模型的性能。 2. 检查参数调整的工作，通过调整模型参数，找到最佳参数使得模型的分类、预测性能最佳。

特征工程需要在机器学习的应用中加深理解一个完整的特征工程、机器学习的处理过程是：应用机器学习的过程包含许多步骤。从问题的定义，到数据的选择和准备，以及模型的准备，模型的评价和调参，最后是结果的表达。这个过程中与我们的话题相关的部分可以用下面几步描述： 1.选择数据：整合数据，规范化到数据集中，集中数据 2.预处理数据：格式化，清理，采样 3.转换数据：特征工程要做的事情 4.建模数据：建立模型，评价模型，调整模型我们看到紧随着特征工程就是建模。这表明，我们做特征工程需要与模型，表现度量相结合。同时也表明，我们需要留下那些适合建模的数据。比如说在最后一步规范化和标准化数据。这看起来是一个预处理的步骤，但实际上他帮助我们意识到对于一个有效模型需要什么样的最终形态。

特征工程的迭代过程：知道特征工程的地位，我们就明确特征工程不是一个孤立的过程。特征工程是一个根据模型评价一次又一次的迭代过程。这个过程主要包括以下几个步骤： 1、头脑风暴：深入了解问题，观察数据，研究特征工程和其他相关问题。 2、设计特征：这个依赖于具体的问题，但是你可能使用自动化的特征提取方式，或者人工构造，或者二者结合。 3、选择特征：使用不同的特征重要性评价指标以及不同的特征选择方法。 4、评价模型：在未知数据集上测试模型性能

认真考虑并且设计在未知数据集上的测试方式。这是对特征工程过程最好的评价方式。

2 回归预测问题

对于连续型目标变量的回归预测问题，评估模型的方法一般有： R^2值 R^2越大，模型的预测效果越好。（后续补充）

3 分类预测问题

对于离散型目标变量的分类预测问题，评估模型的方法一般有：交叉检验观察模型的预测准确率，越大越好。但注意使用决策树或随机森林时的过拟合问题。 AUC、ROC 观察模型的ROC曲线及AUC值，越大越好

七结束语

特征工程做的好，后期的模型调参更容易甚至不用调参，模型的稳定性，可解释性也要更好。如果特征工程做得不好，模型评估怎么调参都调不到理想的效果，那么就需要大量消耗时间继续重复处理、筛选特征，直到模型达到理想的效果。所以，特征工程是一件极其繁琐同时也极其重要的一件事情，至少暂用建模80%以上的时间，所以需要以提升模型的性能和可解释性为目标，有耐心地、逻辑清晰地去做。加油！

八参考资料

数据挖掘之特征工程（笔记）：https://blog.csdn.net/Lee20093905/article/details/79397803 怎样做好特征工程？：https://blog.csdn.net/h2026966427/article/details/80219097 使用sklearn做单机特征工程：http://www.cnblogs.com/jasonfreak/p/5448385.html 机器学习特征工程：https://blog.csdn.net/zehui6202/article/details/79428645 特征工程-数据降维：https://blog.csdn.net/u010865478/article/details/82716992特征工程专题：https://blog.csdn.net/Datawhale/article/details/83033869 Principal component analysis：https://en.wikipedia.org/wiki/Principal_component_analysis?spm=a2c63.p38356.a3.15.6f022c87SkCoPC 特征工程：特征生成，特征选择(三)：https://blog.csdn.net/cymy001/article/details/79169862 特征工程学习笔记：https://github.com/fire717/Machine-Learning/blob/master/other/note/FeatureEngneering.md 关于特征工程：https://blog.csdn.net/a353833082/article/details/50765671 特征工程概述：https://blog.csdn.net/github_36326955/article/details/78738016 特征选择：https://blog.csdn.net/shingle_/article/details/51725054
相关阅读:
第2-1-3章 docker-compose安装FastDFS,实现文件存储服务
 手把手教你使用LabVIEW人工智能视觉工具包快速实现传统Opencv算子的调用(含源码)
游戏设计模式专栏(八）：Cocos中最常见的设计模式之一
 对比两个数组中每个对应位置的元素大小返回每个对比结果组成的列表 numpy.fmin()
【JavaScript】null 和 undefined 的区别
 【malloc详解】| malloc是什么意思以及如何使用
 矢量三维电磁铁的技术参数
 [附源码]计算机毕业设计JAVA“云味坊”购物网站
 改进乌鸦算法求解单目标优化问题
 Layui 表单设计器
原文地址：https://blog.csdn.net/fishmai/article/details/126537719

一 特征工程介绍（Feature Engineering）

1 定义及意义

（1）定义

（2）意义

（3）相关概念

1）特征与属性的区别？

2）什么是特征重要性？

2 流程及方法

二 数据获取

三 数据描述（Feature Describe）

1 数据结构

2 质量检验

标准性、唯一性、有效性、正确性、一致性、缺失值、异常值、重复值

3 分布情况

统计值

探索性数据分析（EDA，Exploratory Data Analysis）

集中趋势、离中趋势、分布形状

四 特征处理（Feature Processing）

1 数据预处理

（1）缺失值处理

1）缺失值删除（dropna）

①删除实例

②删除特征

2）缺失值填充（fillna）

①用固定值填充

②用均值填充

③用众数填充

④用上下数据进行填充

⑤用插值法填充

⑥用KNN进行填充

⑦random forest进行填充

⑧使用fancyimpute包中的其他方法

⑨缺失值作为数据的一部分不填充

（2）异常值处理

1）特征异常平滑

（3）重复值处理

（4）数据格式处理

（5）数据采样

2 特征转换

（1）连续型特征处理

1）函数转换

2）特征缩放

3）无量纲化

①标准化

· 均值方差法

· z-score标准化

· StandardScaler标准化

②归一化

· 最大最小归一化（最常用）

· 对数函数转换（log）

· 反余切转换

③区间缩放法

4）二值化（定量特征）

5）离散化分箱处理(数值型转类别型)

6）不处理

（2）离散型特征处理

1）数值化处理

2）哑编码

①独热编码(one-hot)

②顺序性哑变量

（3）时间序列处理

1）时间戳处理

五 特征选择（Feature Selection）

1 特征检验

（1）单变量

1）正态性检验

2）显著性分析

（2）多变量

1）一致性检验

2）多重共线性

2 特征选择

（1）定义

（2）作用

（3）方法

1）过滤式（Filter）

①方差选择法

②相关系数法

③互信息法

④卡方检验（Chi-Square）

一特征工程介绍（Feature Engineering）

二数据获取

三数据描述（Feature Describe）

四特征处理（Feature Processing）

五特征选择（Feature Selection）

六入模评估

七结束语

八参考资料