-
【LeetCode】栈与单调栈题解汇总
【LeetCode】栈与单调栈题解汇总
写在前面
这里是小飞侠Pan🥳,立志成为一名优秀的前端程序媛!!!
本篇文章同时收录于我的github前端笔记仓库中,持续更新中,欢迎star~
👉https://github.com/mengqiuleo/myNote
20. 有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。示例 1:
输入:s = "()" 输出:true- 1
- 2
示例 2:
输入:s = "()[]{}" 输出:true- 1
- 2
示例 3:
输入:s = "(]" 输出:false- 1
- 2
示例 4:
输入:s = "([)]" 输出:false- 1
- 2
示例 5:
输入:s = "{[]}" 输出:true- 1
- 2
题解思路
- 我们可以让左括号入栈,然后如果遇到右括号,那就取出栈顶的左括号,
- 如果匹配,那就抵消。如果不匹配,返回false
- 如果所有的括号都遍历完了,最后判断栈中还有没有剩余的括号

上图演示了三种不同的情况:
- 字符串里左方向的括号多余了 ,所以不匹配。
- 括号没有多余,但是 括号的类型没有匹配上。
- 字符串里右方向的括号多余了,所以不匹配。
var isValid = function(s) { const stack = []; const map = { "(": ")", "{": "}", "[": "]" } for(const x of s){ if(x in map){// 左括号入栈 //console.log(x);这里只是测试一下x是不是左括号 stack.push(x); continue; } if(map[stack.pop()] !== x) return false;//如果x是右括号,与栈顶元素比较 } return !stack.length; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
71. 简化路径
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 ‘/’ 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (…) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,‘//’)都被视为单个斜杠 ‘/’ 。 对于此问题,任何其他格式的点(例如,‘…’)均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
始终以斜杠 ‘/’ 开头。
两个目录名之间必须只有一个斜杠 ‘/’ 。
最后一个目录名(如果存在)不能 以 ‘/’ 结尾。
此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 ‘.’ 或 ‘…’)。
返回简化后得到的 规范路径 。示例 1:
输入:path = "/home/" 输出:"/home" 解释:注意,最后一个目录名后面没有斜杠。- 1
- 2
- 3
示例 2:
输入:path = "/../" 输出:"/" 解释:从根目录向上一级是不可行的,因为根目录是你可以到达的最高级。- 1
- 2
- 3
示例 3:
输入:path = "/home//foo/" 输出:"/home/foo" 解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。- 1
- 2
- 3
示例 4:
输入:path = "/a/./b/../../c/" 输出:"/c"- 1
- 2
题解思路
首先理解一下题意:
'.'代表当前目录,其实没啥用,比如,/a/./b === /a/b,它是可以去掉的'..'代表的是当前目录的上一个目录,如果出现..,那么它的前一个目录需要去掉。比如,/a/b/../c === /a/c,中间出现了..,那么它前面的/b就要去掉- 而对于例子中的
/home//foo/,需要把//换成/
具体实现
- 首先使用
/将字符串分割,例如 “/home//foo/…/fn” 变成了 [‘home’,‘’,‘foo’,‘…’,‘fn’] - 那么就是会出现:空格(当出现
//时会出现空格),两个点,一个点 - 用栈存储所有路径
- 遍历数组,依次将路径名放入栈中,
- 当出现两个点时说明它的前一个目录需要去掉,那就将栈顶元素取出
- 当出现一个点是,不用管
- 最后再将栈用
/连接返回
var simplifyPath = function(path) { const names = path.split('/'); const stack = []; for(const name of names){ if(name === '..'){ if(stack.length){ stack.pop(); } }else if(name.length && name != '.'){ stack.push(name); } } return '/' + stack.join('/'); };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
注意 两个整数之间的除法只保留整数部分。
可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9- 1
- 2
- 3
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6- 1
- 2
- 3
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释:该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
题解思路
遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
var evalRPN = function(tokens) { const s = new Map([ ['+', (a,b) => a*1 + b*1], ['-', (a,b) => b - a], ['*', (a,b) => b*a], ['/', (a,b) => (b/a)|0] ]) const stack = []; for(const i of tokens){ if(!s.has(i)){ stack.push(i); continue; } stack.push(s.get(i)(stack.pop(), stack.pop())); } return stack.pop(); };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
- MinStack() 初始化堆栈对象。
- void push(int val) 将元素val推入堆栈。
- void pop() 删除堆栈顶部的元素。
- int top() 获取堆栈顶部的元素。
- int getMin() 获取堆栈中的最小元素。
示例 1:
输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]] 输出: [null,null,null,null,-3,null,0,-2] 解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
题解思路
创建两个栈,一个栈是主栈 stack,另一个是辅助栈 minStack,
辅助栈用来存放每个元素对应的:截止到当前元素的最小值
当主栈元素弹出时,辅助栈的元素也要弹出
var MinStack = function() { this.x_stack = []; this.min_stack = [Infinity]; }; /** * @param {number} val * @return {void} */ MinStack.prototype.push = function(val) { this.x_stack.push(val); //当往辅助栈中添加元素时,此时辅助栈中的栈顶存放的是之前所有元素的最小值,然后将当前元素和以前的元素进行比较 this.min_stack.push(Math.min(this.min_stack[this.min_stack.length-1], val)); }; /** * @return {void} */ MinStack.prototype.pop = function() { this.x_stack.pop(); this.min_stack.pop(); }; /** * @return {number} */ MinStack.prototype.top = function() { return this.x_stack[this.x_stack.length-1]; }; /** * @return {number} */ MinStack.prototype.getMin = function() { return this.min_stack[this.min_stack.length-1]; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false] 解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
题解思路
var MyStack = function() { this.queue = []; this.helpQueue = []; }; /** * @param {number} x * @return {void} */ MyStack.prototype.push = function(x) { this.helpQueue.push(x); while(this.queue.length !== 0) { this.helpQueue.push(this.queue.shift()); } while(this.helpQueue.length !== 0){ this.queue.push(this.helpQueue.shift()) } }; /** * @return {number} */ MyStack.prototype.pop = function() { if(this.queue.length !== 0){ return this.queue.shift() } }; /** * @return {number} */ MyStack.prototype.top = function() { if(this.queue.length !== 0){ return this.queue[0]; } }; /** * @return {boolean} */ MyStack.prototype.empty = function() { return this.queue.length == 0; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
-
void push(int x) 将元素 x 推到队列的末尾
-
int pop() 从队列的开头移除并返回元素
-
int peek() 返回队列开头的元素
-
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。示例 1:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
题解思路
var MyQueue = function() { this.s1 = []; this.s2 = []; this.top = null; }; /** * @param {number} x * @return {void} */ MyQueue.prototype.push = function(x) { if(!this.s1.length){ this.top = x; } this.s1.push(x); }; /** * @return {number} */ MyQueue.prototype.pop = function() { if(this.s2.length){ return this.s2.pop(); } while(this.s1.length){ this.s2.push(this.s1.pop()); } return this.s2.pop() }; /** * @return {number} */ MyQueue.prototype.peek = function() { if(this.s2.length){ return this.s2[this.s2.length - 1]; } return this.top; }; /** * @return {boolean} */ MyQueue.prototype.empty = function() { return !this.s1.length && !this.s2.length };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
示例 2:
输入:nums = [1], k = 1 输出:[1]- 1
- 2
题解思路
思路:维护单调递减队列,当进入滑动窗口的元素大于等于队尾的元素时 不断从队尾出队,直到进入滑动窗口的元素小于队尾的元素,才可以入队,以保证单调递减的性质,当队头元素已经在滑动窗口外了,移除队头元素,当i大于等于k-1的时候,单调递减队头就是滑动窗口的最大值

var maxSlidingWindow = function (nums, k) { const q = [];//单递减的双端队列 const ans = [];//最后的返回结果 for (let i = 0; i < nums.length; i++) {//循环nums //当进入滑动窗口的元素大于等于队尾的元素时 不断从队尾出队, //直到进入滑动窗口的元素小于队尾的元素,以保证单调递减的性质 while (q.length && nums[i] >= nums[q[q.length - 1]]) { q.pop(); } q.push(i);//元素的索引入队 while (q[0] <= i - k) {//队头元素已经在滑动窗口外了,移除队头元素 q.shift(); } //当i大于等于k-1的时候,单调递减队头就是滑动窗口的最大值 if (i >= k - 1) ans.push(nums[q[0]]); } return ans; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
946. 验证栈序列
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1] 输出:true 解释:我们可以按以下顺序执行: push(1), push(2), push(3), push(4), pop() -> 4, push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1- 1
- 2
- 3
- 4
- 5
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2] 输出:false 解释:1 不能在 2 之前弹出。- 1
- 2
- 3
题解思路
思路
所有的元素一定是按顺序 push 进去的,重要的是怎么 pop 出来?
假设当前栈顶元素值为 2,同时对应的 popped 序列中下一个要 pop 的值也为 2,那就必须立刻把这个值 pop 出来。因为之后的 push 都会让栈顶元素变成不同于 2 的其他值,这样再 pop 出来的数 popped 序列就不对应了。
算法
将 pushed 队列中的每个数都 push 到栈中,同时检查这个数是不是 popped 序列中下一个要 pop 的值,如果是就把它 pop 出来。
最后,检查不是所有的该 pop 出来的值都是 pop 出来了。
var validateStackSequences = function(pushed, popped) { let stack = []; let i=0, j=0; while(i < pushed.length){ stack.push(pushed[i]); while(stack[stack.length-1] === popped[j] && stack.length){ j++; stack.pop(); } i++; } return stack.length === 0; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
316. 去除重复字母
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证 返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
示例 1:
输入:s = "bcabc" 输出:"abc"- 1
- 2
示例 2:
输入:s = "cbacdcbc" 输出:"acdb"- 1
- 2
题解思路
- 将res作为栈存放字符
- 如果字符已经存在则直接跳过循环
- 由于两个字符直接比较大小会根据字典序输出true/false
- 所以直接将循环字符和栈顶元素比较,如果栈顶元素大于当前字符且后续还有其他字符可以作为替代时,栈顶元素出栈
- 当前元素入栈
var removeDuplicateLetters = function(s) { let res = []; for(let i=0;i<s.length;i++){ if(res.includes(s[i])) continue; while(res[res.length-1] > s[i] && s.indexOf(res[res.length-1], i) > i){ res.pop(); } res.push(s[i]); } return res.join(''); };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2]- 1
- 2
示例 2:
输入: nums = [1], k = 1 输出: [1]- 1
- 2
题解思路
Map + 桶排序
- 利用Map的key和value值保存整数和频率关系
- 若元素数量小于等于k -> 直接返回key的数组
- 若大于 -> 桶排序(具有不同整数,相同频率情况)
- 用数组存放具有相同频率的数:key为频率,value为一个数组,里面放所有的具有key频率的数
- 相同频率时 -> 将整数放入该频率的桶
不同频率时 -> 创建一个新桶放入 - 最后倒序排序将桶一个个拿出 -> 至到拿到第k个整数
let topKFrequent = function(nums, k) { // 利用Map来记录key-整数和value-频率的关系 let map = new Map() nums.map((num) => { if (map.has(num)) map.set(num, map.get(num) + 1) else map.set(num, 1) }) // 如果元素数量小于等于k -> 直接返回字典key-整数 if(map.size <= k) { return [...map.keys()] } // 返回桶排序结果 return bucketSort(map, k) }; // 桶排序 let bucketSort = (map, k) => { let arr = [], res = [] map.forEach((value, key) => { // 利用映射关系(出现频率作为下标)将数据分配到各个桶中 if(!arr[value]) { // key的数组 -> 有不同整数,相同频率的情况 arr[value] = [key] } else { // 相同频率时 arr[value].push(key) } }) // 从大到小遍历频率,最大频率为数组的末尾,如果当前频率存在,那就将它放入答案数组 for(let i = arr.length - 1; i >= 0 && res.length < k; i--){ // 若有数据 -> 放入该数组 if(arr[i]) { res.push(...arr[i]) } } return res }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
456. 132 模式
给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i < j < k 和 nums[i] < nums[k] < nums[j] 。
如果 nums 中存在 132 模式的子序列 ,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,4] 输出:false 解释:序列中不存在 132 模式的子序列。- 1
- 2
- 3
示例 2:
输入:nums = [3,1,4,2] 输出:true 解释:序列中有 1 个 132 模式的子序列: [1, 4, 2] 。- 1
- 2
- 3
示例 3:
输入:nums = [-1,3,2,0] 输出:true 解释:序列中有 3 个 132 模式的的子序列:[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。- 1
- 2
- 3
题解思路
所谓「单调栈」就是栈中的元素都是依次递增或者递减的 如 [4, 3, 2, 1]
- 132模式至少存在三个数字 分别为 min, max, med
- min, max, med 顺序不可调换
- 遍历数组找 med 的位置
- 本题用单调栈存储 max 位置的值
- 从后向前遍历数组
- 如果当前遍历大于栈顶元素 则栈的单调性被破坏,清空栈 将当前值作为max并压入栈底, 将栈底元素作为med
- 如果 med max 都存在,遍历到 比med小的值 可放入min位置 返回true
- 因为在循环中会进行当前值和med值的比较
if(nums[i] < med),所以med 初始值设置为理论最小值,
举例:
初始化如下:
并且从后往前遍历
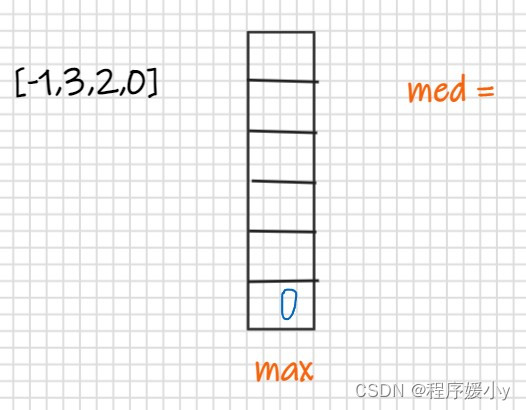
然后遍历到2,此时当前值大于栈顶元素,清空栈,并将栈底元素作为med值,当前值作为max压入栈,
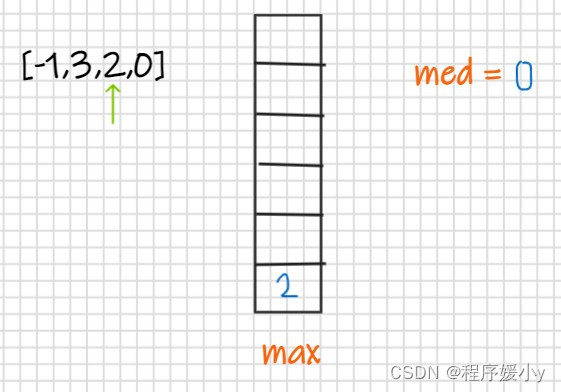
继续向前遍历,当前值为3,大于栈顶元素,重复上面的步骤
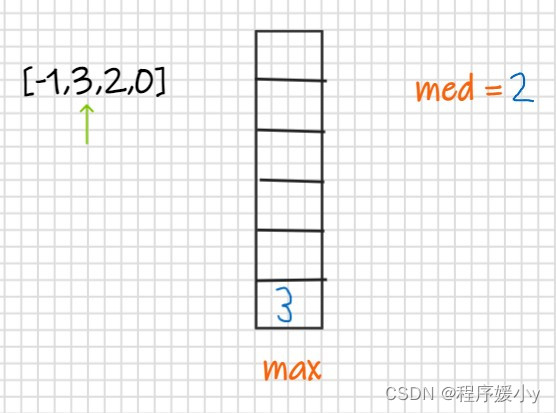
继续向前遍历,当前值为-1,小于med,所以返回true
var find132pattern = function(nums) { let stack = [], med = -Infinity; for(let i=nums.length-1; i >=0; i--){ if(nums[i] < med) return true; while(stack.length>0 && stack[stack.length-1] < nums[i]){ med = stack.pop(); } stack.push(nums[i]); } return false; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2]. 输出:[-1,3,-1] 解释:nums1 中每个值的下一个更大元素如下所述: - 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。 - 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。 - 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。- 1
- 2
- 3
- 4
- 5
- 6
- 7
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4]. 输出:[3,-1] 解释:nums1 中每个值的下一个更大元素如下所述: - 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。 - 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。- 1
- 2
- 3
- 4
- 5
- 6
题解思路
参考思路:
var nextGreaterElement = function(nums1, nums2) { let map = new Map(), stack = [], ans = []; nums2.forEach(item => { while(stack.length && item > stack[stack.length-1]){ map.set(stack.pop(), item); } stack.push(item); }) stack.forEach(item => map.set(item, -1)); nums1.forEach(item => ans.push(map.get(item))); return ans; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
503. 下一个更大元素 II
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1] 输出: [2,-1,2] 解释: 第一个 1 的下一个更大的数是 2; 数字 2 找不到下一个更大的数; 第二个 1 的下一个最大的数需要循环搜索,结果也是 2。- 1
- 2
- 3
- 4
- 5
示例 2:
输入: nums = [1,2,3,4,3] 输出: [2,3,4,-1,4]- 1
- 2
题解思路
我们可以使用单调栈解决本题。单调栈中保存的是下标,从栈底到栈顶的下标在数组 nums 中对应的值是单调不升的。
每次我们移动到数组中的一个新的位置 i,我们就将当前单调栈中所有对应值小于 nums[i] 的下标弹出单调栈,这些值的下一个更大元素即为 nums[i](证明很简单:如果有更靠前的更大元素,那么这些位置将被提前弹出栈)。随后我们将位置 i 入栈。
但是注意到只遍历一次序列是不够的,例如序列 [2,3,1],最后单调栈中将剩余 [3,1],其中元素 [1] 的下一个更大元素还是不知道的。
一个朴素的思想是,我们可以把这个循环数组「拉直」,即复制该序列的前 n-1 个元素拼接在原序列的后面。这样我们就可以将这个新序列当作普通序列,用上文的方法来处理。
而在本题中,我们不需要显性地将该循环数组「拉直」,而只需要在处理时对下标取模即可。
举例
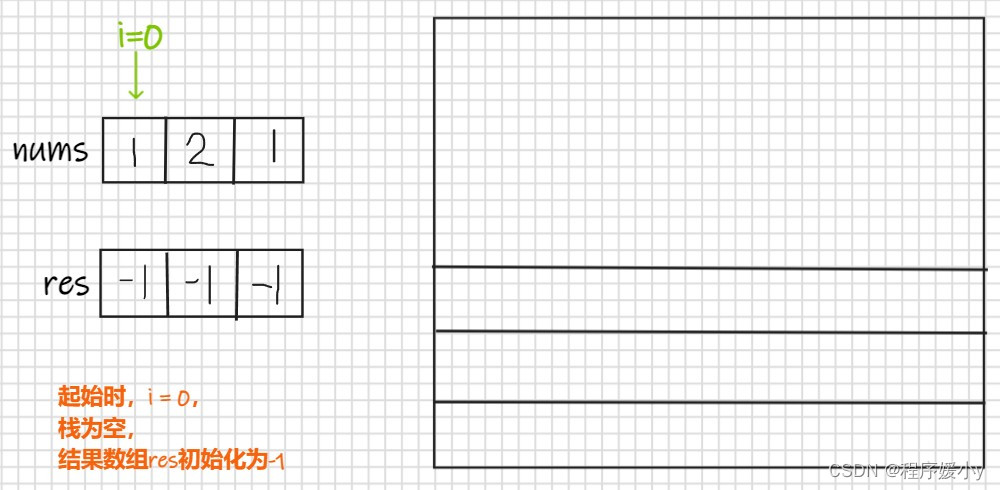
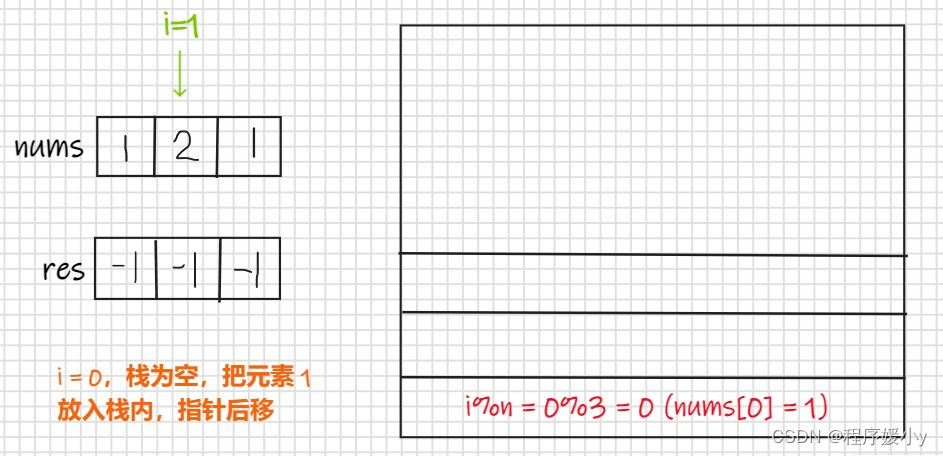
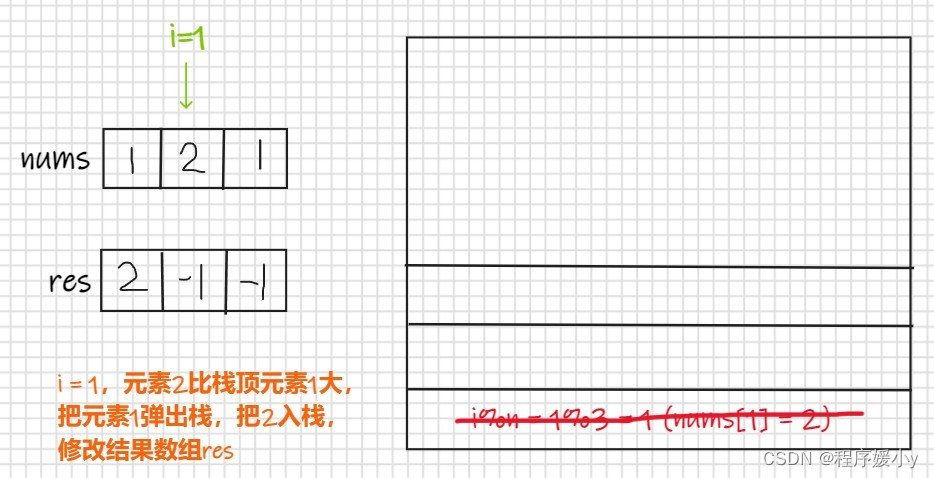
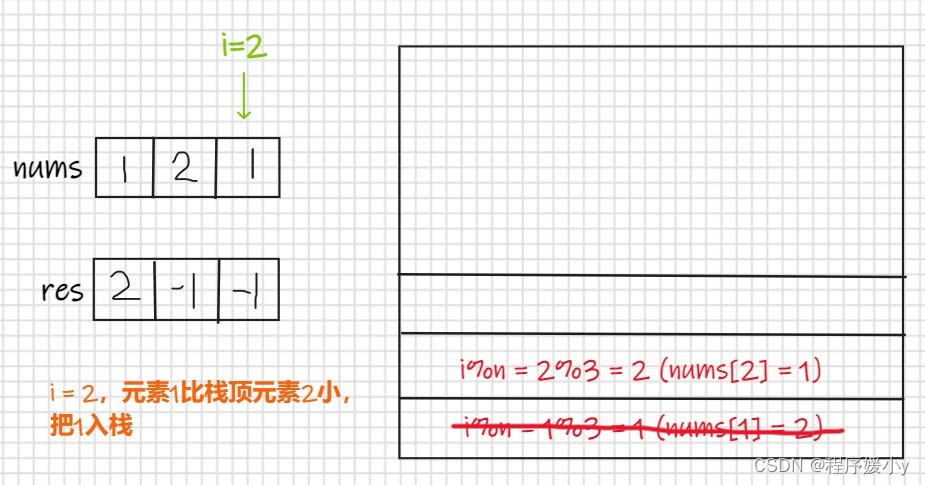
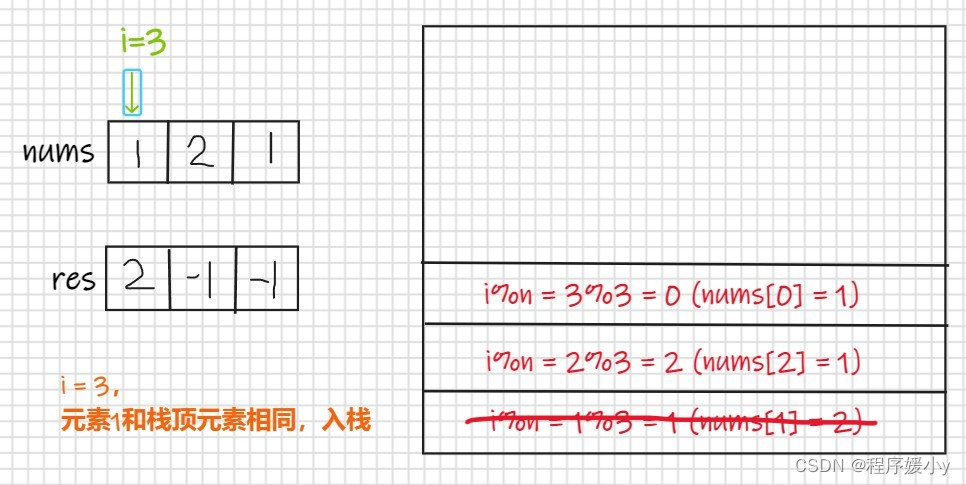
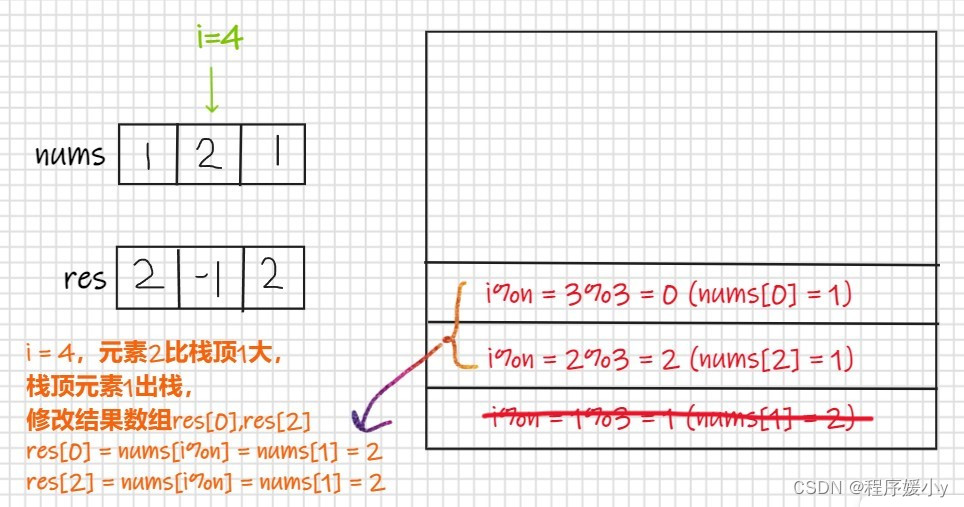
var nextGreaterElements = function(nums) { const n = nums.length; const ret = new Array(n).fill(-1); const stk = []; for (let i = 0; i < n * 2 - 1; i++) { while (stk.length && nums[stk[stk.length - 1]] < nums[i % n]) { ret[stk[stk.length - 1]] = nums[i % n]; stk.pop(); } stk.push(i % n); } return ret; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
581. 最短无序连续子数组
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
输入:nums = [2,6,4,8,10,9,15] 输出:5 解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。- 1
- 2
- 3
示例 2:
输入:nums = [1,2,3,4] 输出:0- 1
- 2
示例 3:
输入:nums = [1] 输出:0- 1
- 2
题解思路
- 将数组的值先克隆一份并排序
- 比较新数组和原数组的值,找出不同元素出现的开始位置和结束位置
- 两者距离就是我们要的结果
var findUnsortedSubarray = function(nums) { let snums = nums.slice(); snums.sort((a,b) => a-b); let start = nums.length, end = 0; for(let i=0; i<nums.length;i++){ if(snums[i] !== nums[i]){ start = Math.min(start, i); end = Math.max(end, i); } } return end-start > 0 ? end-start+1 : 0; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73] 输出: [1,1,4,2,1,1,0,0]- 1
- 2
示例 2:
输入: temperatures = [30,40,50,60] 输出: [1,1,1,0]- 1
- 2
示例 3:
输入: temperatures = [30,60,90] 输出: [1,1,0]- 1
- 2
题解思路
var dailyTemperatures = function(temperatures) { let ans = new Array(temperatures.length).fill(0); let stack = []; for(let i=0; i < temperatures.length; i++){ while(stack.length && temperatures[i] > temperatures[stack[stack.length - 1]]){ let t = stack[stack.length - 1]; stack.pop(); ans[t] = i - t; } stack.push(i); } return ans; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
1047. 删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入:"abbaca" 输出:"ca" 解释: 例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"- 1
- 2
- 3
- 4
题解思路
var removeDuplicates = function(s) { const stack = []; for(const x of s){ let c = null; // 如果x=c,那就取出c,并且x不放入栈中 if(stack.length && x === (c=stack.pop())) continue; c && stack.push(c); stack.push(x); } return stack.join(""); };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
-
相关阅读:
Java中的this关键字
Java的jmap命令使用详解
VMware虚拟机 Centos7 配置静态IP和DNS
抢先体验!星河社区ERNIE Bot SDK现已支持文心大模型4.0
小谈设计模式(21)—迭代器模式
基于PHP+MySQL汽车查询系统的设计与实现
LabVIEW开发气体调节器
vue3+ts项目04-国际化
vue3 electron 打包后进程通信无效,开发环境正常
[附源码]计算机毕业设计springboot基于Web的绿色环保网站
- 原文地址:https://blog.csdn.net/weixin_52834435/article/details/126530586
