目标检测：Generalized Focal Loss V2（CVPR2020）

Generalized Focal Loss V2: Learning Reliable Localization Quality Estimation for Dense Object Detection
CCF-A
Xiang LiWenhai WangXiaolin HuJun LiJinhui TangJian Yang
computer vision and pattern recognition arXiv: Computer Vision and Pattern Recognition Nov 2020

基于GFL v1

很显然，这篇文章书接上回
作者在v1中提出了GFL（包含优化带分类任务的QFL和优化回归任务的DFL），其回归任务是基于离散概率分布估计做的，很是巧妙。在v2中，作者基于v1中回归任务的离散概率分布估计，对回归任务进行质量评估，以帮助NMS时保留到回归质量最好的边界框。其直观的原理是这样的：估计的离散概率分布越平滑，那不确定性越高，网络对得到的框的质量是表示怀疑的，概率分布越尖锐，表示确定性很高，网络很笃定回归得到的边界框。

GFL v2的具体实现

作者在文中说，在NMS是所用的排位分数J可以按下式分解：
J = C × I
C代表分类分数向量，I代表回归质量，是一个标量（估计的当前预测框与gt框的IoU），这样J就是分类与回归质量的联合表征。

我们直接看它怎么具体实现的，首先上网络检测头的结构图：

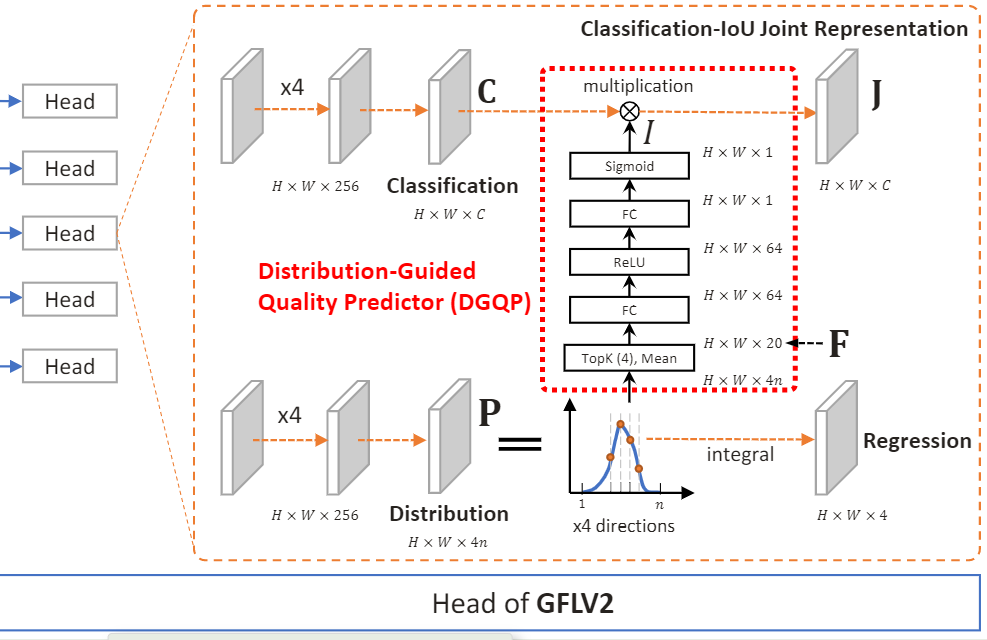
回归分支得到了4个离散概率分布P，在每一个p中，取最高的k个概率值（Top-k），以及这k个概率值的均值，
得到H×W×4×(k+1)特征，文中k取4，那么就得到了H×W×20大小的特征F，然后按照FC，ReLU，FC，Sigmoid的顺序进行特征提取，中间隐藏层的通道数设置为了64，最终得到一个标量I，与分类向量C进行相乘，得到具有回归质量感知的分类结果J。

如上图，使用均值对P分布的相对偏移不敏感，其实也可以使用方差等，但效果没均值好。

训练还是和v1同样的策略，分类和回归两个分支分别使用QFL和DFL损失。

GFL进行回归质量评估的路子与前述工作很不一样，这算是最大的创新点，实现的细节还是很简单和轻量化的，这也让其在训练和推理时只会占用很少的计算资源，并且作为一个附加的模块可以很方便地应用到现有的检测器上。

我的感受：

目标检测刚开始是分类和回归不解耦的，即基于同一个支路的特征进行两个任务的实现，之后发展到解耦头，性能提升，但到了现在，如VarfocalNet，GFL这些文章，又是在积极探寻分类与回归之间的关联性，以帮助NMS拿到更准确的分数排位。