Matlab彩色图像卷积的数学原理及纯手工实现

一、引言

在图像处理中，不论是提取图像边缘特征，还是尺度空间变换，亦或者目前大火的深度学习，图像卷积都是非常重要的基础工作。卷积从整体上说是卷积，从局部上说其实就是内积。卷积不论在数学上还是信号处理中都有非常重要的应用，主要目的是用来做图像滤波、特征提取和多尺度分解等。可以这么说，不会卷积就是不会图像处理。本文给出了图像卷积的数学原理及Matlab手工实现，此外还给出Matlab内部函数imfilter的用法。

二、卷积的数学原理

对于给定的两个一元可积函数f(x)和g(x)，其卷积定义为：

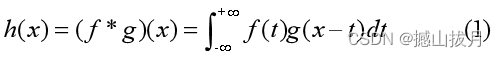
离散化的结果为：

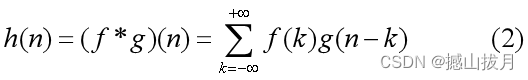
此时，可以称f(x)为滤波器，或者卷积核，g(x)是已知的信号。
推广到二元函数情形，其离散形式的卷积为：

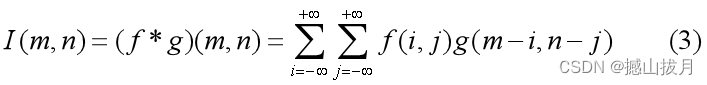
由于数字图像的像素是一个矩阵，所以可以使用上述公式(3)来实现卷积。
通过上述公式，可以发现，当固定(m,n)时，则右端就是内积的表达式了。所以我在前面说卷积的局部就是内积（当然了，这仅仅是我自己的说法，而且这里的局部其实是对固定的点而言，可不是一个局部区域啊）。下图演示了卷积。

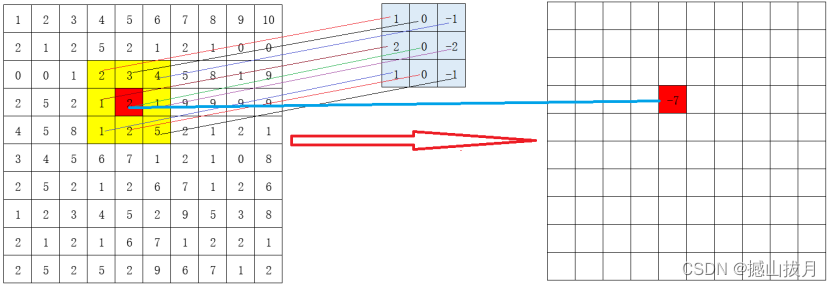
现在想计算红色2处的卷积值，则把中间的3x3卷积核扣到以2为中心的黄色区域，做内积得到-7存放到右侧红色位置。其它位置的卷积也是如此计算。

至此，是不是发现了卷积原来如此简单，难怪其在图像处理中具有广泛的应用。
有人可能会问，卷积核都是怎么选取的，我的回答是“看实际需要”，如果是低通滤波，则选取低通滤波器，例如高斯低通滤波器，其作为卷积核可以让图像变得平滑甚至模糊。下图就是利用3x3和5x5高斯卷积核对图像做卷积的结果。

其中左侧图是带有噪声的原始图像，中间图是使用3x3高斯卷积和滤波的结果，右图是使用5x5高斯卷积和滤波的结果，从图中可以看出卷积核模板越大，则去噪效果越好。（到此你又学会了一招，图像的低通滤波可以去噪）

三、Matlab纯手工实现图像卷积

1.单通道图像卷积

function convImage = SingleConvolution( image, filter )
%功能：
%   单通道图像的卷积运算
%输入参数： 
%   image：扩展后的图像
%   filter：滤波器
%输出参数： 
%   imageConv：卷积后的图像
[Height, Width] = size( image );
[mF, nF] = size( filter );
for i = 1 : Height - mF + 1
    for j = 1 : Width - nF + 1
        localImage = [];
        localImage = image(i:i+mF-1, j:j+nF-1);
        convImage(i, j) = sum( sum( localImage .* filter ) );
    end
end
convImage = uint8( convImage );
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2.灰度图像或彩色图像的卷积

function eIm = ImageConlutionFun( image, filter )
imSize = size( image );
dim = numel( imSize ); %图像的维数
if dim == 2
    eIm =  SingleConvolution( image, filter );
else
    imR = image( :, :, 1 );
    imG = image( :, :, 2 );
    imB = image( :, :, 3 );
    eImR =  SingleConvolution( imR, filter );
    eImG =  SingleConvolution( imG, filter );
    eImB =  SingleConvolution( imB, filter );
    eIm = cat(3 ,eImR, eImG, eImB );%将三个颜色分量合成彩色图像
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

3.灰度图像卷积Demo_1

%利用sobel算子提取图像的边缘特征
clear all
clc
image = double( imread( 'lena.bmp' ) );
filterY = double( fspecial( 'sobel' ) );%sobel卷积核
filterX = filterY';
imageConvY = ImageConlutionFun( image, filterY );
imageConvX = ImageConlutionFun( image, filterX );
imageConv = max( imageConvY, imageConvX );
figure; imshow( uint8(image) )
figure; imshow( imageConv )
1
2
3
4
5
6
7
8
9
10
11

运行结果如下：

4.灰度图像卷积Demo_2

%图像低通滤波
clear all
clc
image = double( imread( 'lenaNoise.bmp' ) );
filter = double( fspecial( 'gaussian', [5,5], 1 ) );%gaussian卷积核
imageConv = ImageConlutionFun( image, filter );
size( image )
size( imageConv )
figure; imshow( uint8(image) )
figure; imshow( imageConv )
1
2
3
4
5
6
7
8
9
10

运行结果如下：

5.彩色图像卷积Demo_3

%图像低通滤波
clear all
clc
image = double( imread( 'cloud.jpg' ) );
filter = double( fspecial( 'gaussian', [7,7], 1 ) );%gaussian卷积核
imageConv = ImageConlutionFun( image, filter );
figure; imshow( uint8(image) )
figure; imshow( imageConv )
1
2
3
4
5
6
7
8

运行结果如下：

说明：从上述运行结果可以看出，卷积之后图像的尺寸比原图像小，这是因为没有做padding造成的，如果在做卷积之前增加一项padding工作，则可以解决此问题，例如demo_3的代码修改为：

clear all
clc
image = double( imread( 'cloud.jpg' ) );
filter = double( fspecial( 'gaussian', [7,7], 1 ) );%gaussian卷积核
[m, n] = size( filter );
im = padarray( image, [floor(m/2), floor(n/2)], 'symmetric' );%图像padding
imageConv = ImageConlutionFun( im, filter );
size( image )
size( imageConv )
figure; imshow( uint8(image) )
figure; imshow( imageConv )
1
2
3
4
5
6
7
8
9
10
11

则运行结果如下：

此时卷积前后图像的尺寸是相同的。

四、Matlab卷积函数imfilter

imfilter( Image, filter, boundarymode )
Image：图像像素矩阵
filter：卷积核矩阵
boundarymode：X 边界延拓为X，缺省值为0,其取值有：
Symmetric： 镜像延拓边界
Replicate： 最近邻延拓边界
Circular： 周期延拓边界
例如：

clear all
clc
im = imread( 'cloud.jpg' );
filter = fspecial( 'gaussian' ,[3,3], 1 );
imconv = imfilter( im, filter, 'symmetric' );
figure;imshow(im)
figure;imshow(imconv)
1
2
3
4
5
6
7

运行结果如下：