大家好！我是沐曦希💕

---

给大家介绍一款超牛的斩获大厂offer利器——牛客网

1. 小乐乐与字符串

题目链接： BC119 小乐乐与字符串

思路

1.暴力枚举超时。
2.抓住“CHN”字符串只有三个字符这个特点。
3.统计C的数量countC
4.每遇到一个H字符，就能构成countC数量的CH串，countCH += countC
5.每遇到一个N字符，就能构成countCH数量的CHN串，所以ans += countCH
6.最后的结果就是ans

解法一：创建一个数组来存储该字符串，通过指针变量来访问该字符串，并通过指针变量不断加一来访问所有的字符串，并通过if来判断指针变量所指的字符是否为C,H,N来是否加一
解法二：创建一个数组来存储该字符串，通过for或者while语句来实现访问所有的字符串。

代码

//code1
#include
int main() 
{
    char s[8001] = {'\0'};
    gets(s);
    char* ps = s;
    long long count = 0;
    long long c = 0;
    long long h = 0;
    while (*ps != '\0') 
    {
        if (*ps == 'C')
         {
            c++;
        } else if (*ps == 'H')
            h += c;
        else if (*ps == 'N')
            count += h;
        ps++;
    }
    printf("%lld\n", count);
    return 0;
}
//code2
#include 
#include 
int main()
{
    char str[8005];
    gets(str);
    long long i,cnt_c=0,cnt_h=0,cnt_n=0;
    for(i=0;str[i]!='\0';i++)
    {
        if(str[i]=='C') cnt_c++;
        else if(str[i]=='H') cnt_h+=cnt_c;
        else if(str[i]=='N') cnt_n+=cnt_h;
        //printf("%c",str[i]);
    }
    printf("%lld\n",cnt_n);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

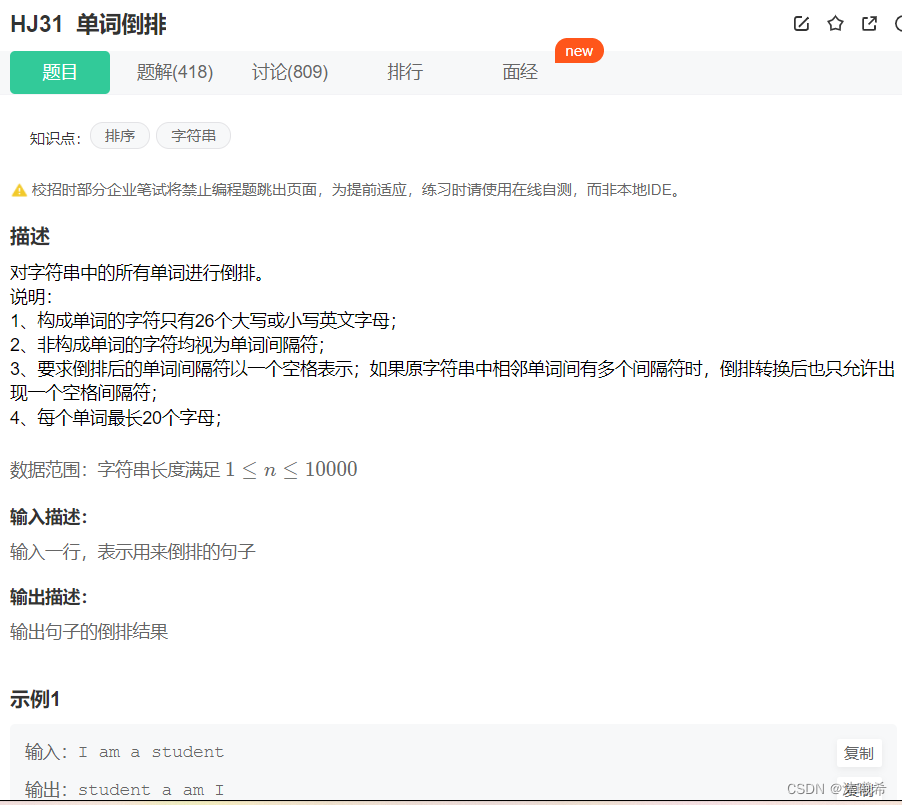
2.单词倒排

题目链接:HJ31 单词倒排

思路

定义一个字符指针数组，用于保存每个单词的起始字符地址，接下来将非字母字符全部替换成为字符串结尾标志，则单词字符字母遇到结尾就结束了，相当于把一个字符串以非字母字符进行切割成为了多个字符串，最终对字符指针数组进行逆序打印每个单词即可。

代码

#include 
#include 
int main()
{
	char str[10001] = { 0 };//字符串最长10000
	int row = 0;
	while (gets(str) > 0) 
	{
		char* ptr = str;
		char* word[10000] = { NULL };
		while (*ptr != '\0') 
		{
			//如果是个字母字符，则是单词的起始字符
			if (('z' >= *ptr && *ptr >= 'a') || ('Z' >= *ptr && *ptr >= 'A')) 
			{
				word[row++] = ptr;//保存每个单词的起始地址
				//把本次的单词字母字符走完，直到遇到非字母字符
				while (*ptr != '\0' &&
					(('z' >= *ptr && *ptr >= 'a') || ('Z' >= *ptr && *ptr >= 'A'))) 
				{
					ptr++;
				} 
				continue;//不能继续向下，因为下边的ptr++会跳过当前的非字母字符
			} 
			*ptr = '\0';//把非字母的数据全部替换为结尾标志
			ptr++;
		} 
		for (int i = row - 1; i >= 0; i--) 
		{
			printf("%s ", word[i]);//针对所有单词的起始地址逆序开始打印即可
		} 
		printf("\n");
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

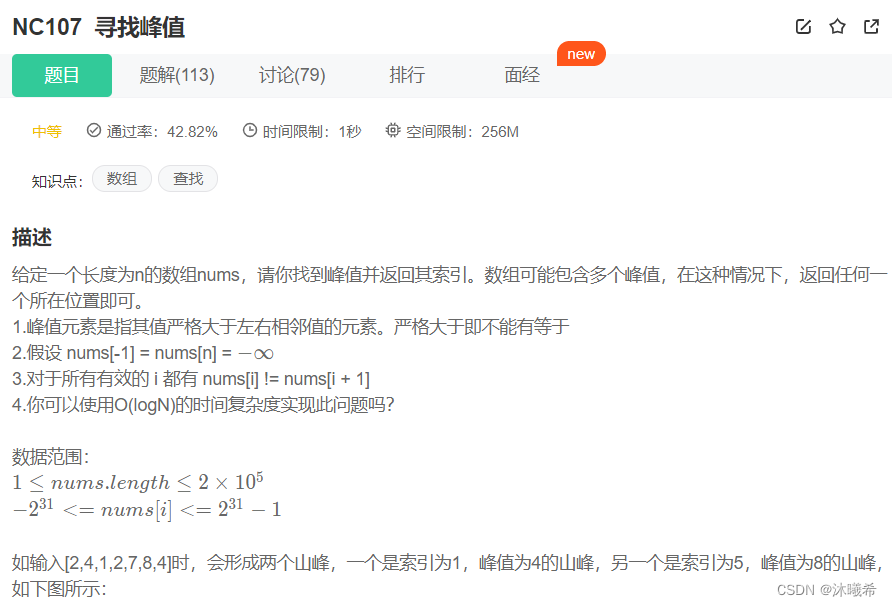
3.寻找峰值

题目链接:NC107 寻找峰值

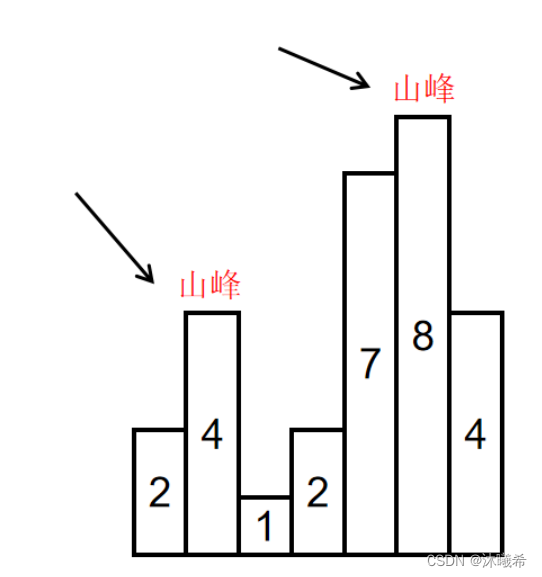
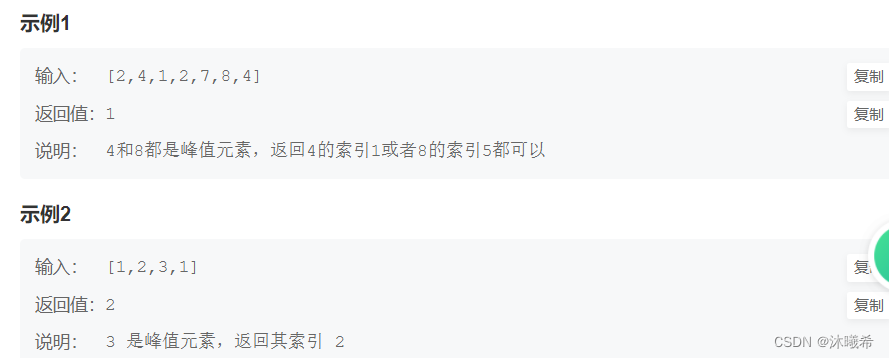
思路

暴力破解： 遍历数组，从 [1，n-1] 号位置开始，哪个位置的数据大于上一个数据和下一个数据即可。
更优思想：二分思想，中间比右边大，认为从右往左半边递增，则把 right 不断向左靠拢 right=mid ，注意不能是 mid-1 ，因为这个位置
有可能就是峰值点。
直到遇到中间比右边小了，意味着数据开始递降了，则 left 向右偏移， left=mid+1 ; 而一旦 mid+1 位置大于了right ，意味着刚好这个 mid+1 位置，是一个左半边-右往左递降，右半边-右往左递增的点，就是一个峰值点。
示例：

int arr[] = {3, 5, 4, 4, 3, 2, 1} , 这个数组中两边边界都是非峰值点
int left = 0, right = 6;
left=0,right=6,mid=3: arr[3]=4 > arr[4]=3, 则right = mid = 3; //从右往左是递增的
left=0,right=3,mid=1: arr[1]=5 > arr[2]=4, 则right = mid = 1; //从右往左是递增的
left=0,right=1,mid=0: arr[0]=3 < arr[1]=5, 则left = mid + 1 = 1; //从右往左开始递降了
left > right 退出循环， 返回left，也就是1号下标位置
1
2
3
4
5
6

代码

int findPeakElement(int* nums, int numsLen) {
	//边界情况处理，1个元素前后都是负无穷 以及 0号位置大于1号位置，-1位置负无穷的情况
	if (numsLen == 1 || nums[0] > nums[1]) return 0;
	//末尾位置数据大于上一个位置数据，而nums[numsLen]负无穷的情况
	if (nums[numsLen - 1] > nums[numsLen - 2]) return numsLen - 1;
	int left = 0, right = numsLen - 1, mid;
	while (left < right) {
		mid = left + (right - left) / 2;
		if (nums[mid] < nums[mid + 1])//中间比右边小，意味着右边肯定有个峰值
			left = mid + 1;
		else //否则在左边包括当前位置肯定有个峰值
			right = mid;
	} 
	return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4.写在最后

那么就到这里了。