寒假训练——第三周（线性DP）

A - 数塔问题

A - 数塔问题
思路：

• 数字三角形模型

代码如下：

#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 210, M = 2e5 + 10;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m;
int f[N][N];

void solve()
{
    cin >> n;
    
    memset(f, 0, sizeof f);
    
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            cin >> f[i][j];
            
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )  
            f[i][j] += max(f[i - 1][j - 1], f[i - 1][j]);
    
    int res = -1;
    for (int i = 1; i <= n; i ++ )  
        res = max(res, f[n][i]);
        
    cout << res << endl;
    
    return;
}

signed main()
{
    //fast;
    T = 1;
    //cin >> T;
    
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

---

B - 最长上升子序列

B - 最长上升子序列

思路：

• 最长上升子序列模型（ $longestincreasingsequence$ ），又称 $LIS$ 模型

代码如下：

#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 2100, M = 2e5 + 10;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m;
int a[N];
int f[N];

void solve()
{
    cin >> n;
    
    for (int i = 1; i <= n; i ++ )  
        cin >> a[i];
    
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++ )
            if(a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
    }
    
    int res = 0;
    for (int i = 1; i <= n; i ++ )
        res = max(res, f[i]);
        
    cout << res << endl;
    
    return;
}

signed main()
{
    //fast;
    T = 1;
    //cin >> T;
    
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

---

C - 最长公共子序列 ( $LCS$ )：$O(nlogn)$做法

全称：( $longestcommonsequence$ )

C - 最长公共子序列

前提：

• 最长公共子序列至少有一个序列元素不重复

思路：

• 最长公共子序列（ 转化为 最长上升子序列
• 按照 最长上升子序列的优化方案一 （点此链接看详细证明）：贪心 + 二分 优化为 $O(nlogn)$

具体步骤：

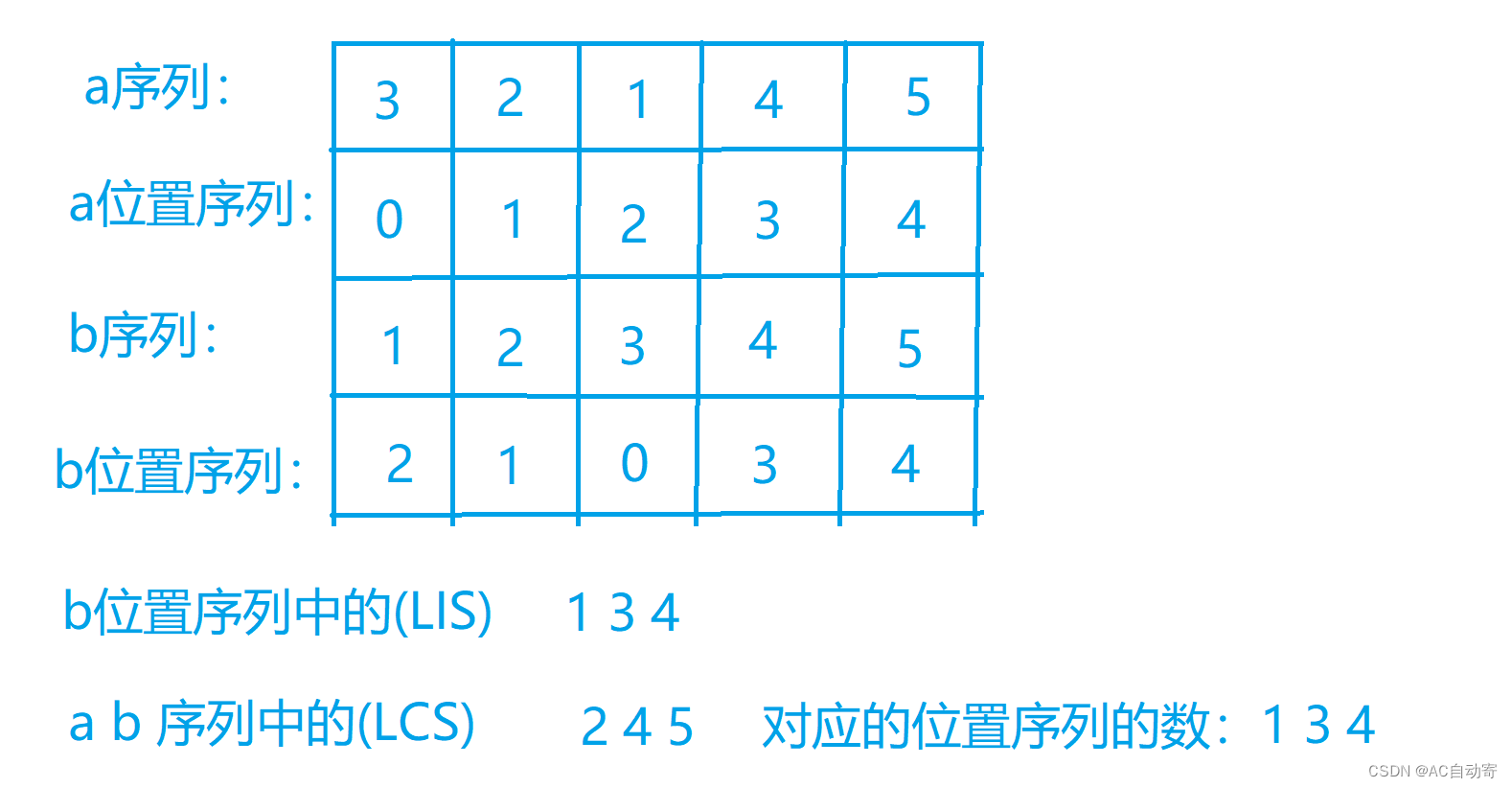
• 将元素不重复的序列的元素映射到其下标
• 在第二个序列中找到每个元素在第一个序列中的下标，构造新序列，
• 我们要求的结果即为新序列的 最长上升子序列( $LIS$ )

证明：

• 找 最长公共子序列 只需维护数据的相对位置关系即可

举例：

• input:

  5 
  3 2 1 4 5
  1 2 3 4 5
  1
  2
  3

• output:

  3
  1

• 如图：
  

代码如下：

#include 
#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int n;
int id[N], q[N];

int main()
{  
    scanf("%d", &n);
    
    memset(id, -1, sizeof id);
    
    for (int i = 0; i < n; i ++ )
    {
        int x;
        scanf("%d", &x);
        id[x] = i;
    }
    
    int len = 0;
    q[0] = -1; 
    // 位置序列中最小值为 0 ，所以设置一个比最小值还小的值 -1 作为哨兵，
    // 防止数组越界，保证了在二分的时候一定能找到结果
    
    for (int i = 0; i < n; i ++ )
    {
        int x;
        scanf("%d", &x);
        if(id[x] == -1) continue;
        int k = id[x];
        int l = 0, r = len;
        while(l < r)
        {
            int mid = l + r + 1 >> 1;
            if(q[mid] < k) l = mid;
            else r = mid - 1;
        }
        
        q[r + 1] = k;
        len = max(len, r + 1);
    }
    
    printf("%d\n", len);
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

---

D - 摘花生

D - 摘花生

思路：

• 模拟，，水题

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 110, M = 1e5 + 10;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

struct Points
{
    int x, y, w;
    bool operator < (const Points &W)const
    {
        return W.w < w;
    }
}g[M];

int idx;

void solve()
{
    memset(g, 0, sizeof g);
    idx = 0;
    
    cin >> n >> m >> times;
    
    int x;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            cin >> x;
            if(x > 0) g[idx ++ ] = {i, j, x};
        }
        
    sort(g, g + idx);
    
    int res = 0;
    int lastx = 0, lasty;
    for (int i = 0; i < idx; i ++ )
    {
        if(!i) lasty = g[i].y;
        
        int t = abs(g[i].x - lastx) + abs(g[i].y - lasty);
        
        if(times >= g[i].x + t + 1)
        {
            times -= t + 1;
            res += g[i].w;
            lastx = g[i].x, lasty = g[i].y;
        }
        else break;
    }
    
    cout << res << endl;
    
    return;
}

signed main()
{
    //fast;
    T = 1;
    cin >> T;
    
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

---

E - Boxes of Chocolates Again

E - Boxes of Chocolates Again

思路：

• 完全背包求方案数 + 高精度加法

问： 高精度用 $vector$ 慢的一批，不管了（这题没啥意思，，）思路就是这样，有高人救一下否 $?$

答： 高精度压位即可，$int$类型 只存 0~9 的一位数实在是浪费，并且速度还慢，$int$ 类型习惯压 $4$ 或 $8$ 位，最多可以压 $9$ 位。

注： 想学习高精度压位的，参考此博客：【算法专题】高精度之压位
写的确实不错啊，膜拜 dalao ! ! !

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 5500, M = N * 2;
const int YB = 8, YM = 1e8;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, times;

vector<int> f[N];

vector<int> add(vector<int> &A, vector<int> &B)
{
    if(A.size() < B.size()) return add(B, A);
    
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % YM);
        t /= YM;
    }
    
    if(t) C.push_back(t);
    
    return C;
}

void print(vector<int> f)
{
    printf("%d", f.back());
    for (int i = f.size() - 2; i >= 0; i -- )
        printf("%08d", f[i]);
    printf("\n");
}

void init()
{
    f[0].push_back(1);
    for (int i = 1; i <= 5010; i ++ )
        for (int j = i; j <= 5010; j ++ )
            f[j] = add(f[j], f[j - i]);
    
    return;
}

void solve()
{
    print(f[n]);
}

signed main()
{
    //fast;
    T = 1;
    //cin >> T;
    
    init();
    
    while(cin >> n)
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

---

F - Road Optimization

F - Road Optimization

思路：

• 
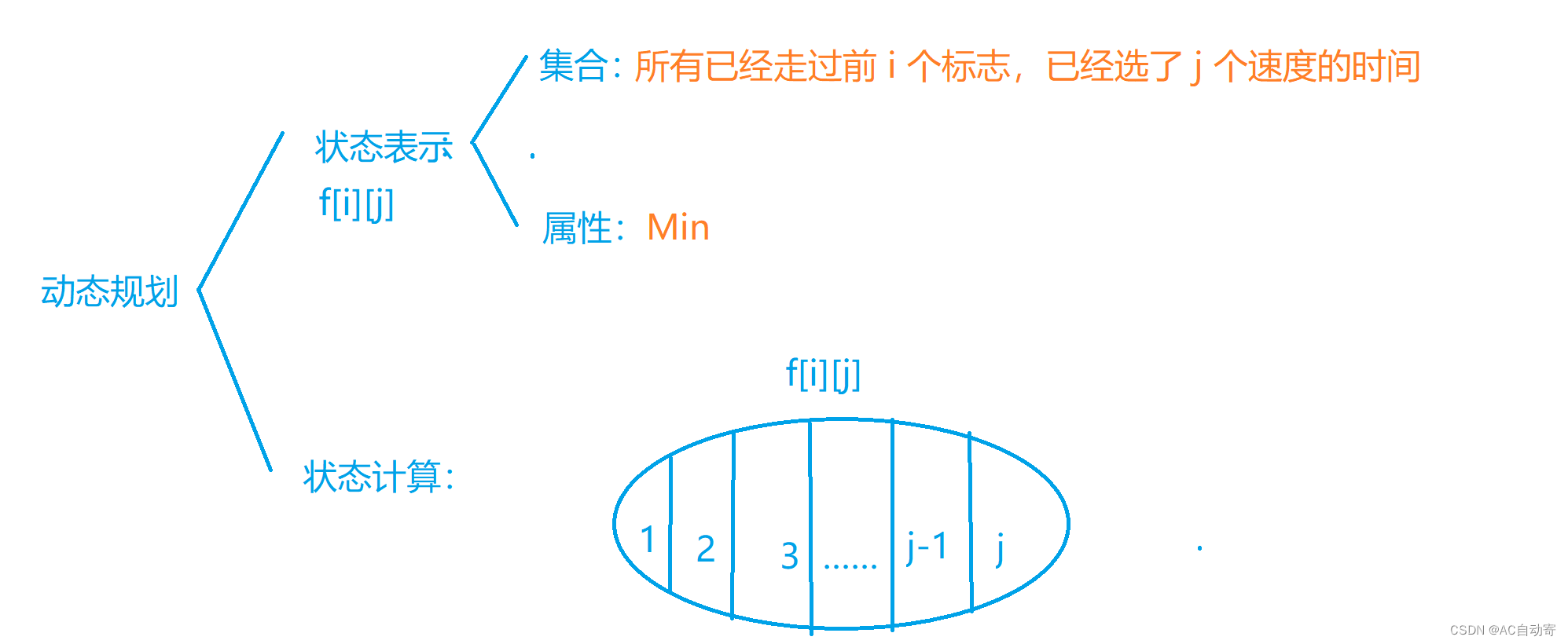
• 直接枚举 $f[i][j]$ 是从哪一次转移过来的即可

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 510, M = N * 2;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, allow;
int dist[N];
int speed[N];
int f[N][N];

void solve()
{
    cin >> n >> m >> allow;
    
    for (int i = 1; i <= n; i ++ )
        cin >> dist[i];
    for (int i = 1; i <= n; i ++ )
        cin >> speed[i];
    
    dist[ ++ n] = m;
    
    memset(f, 0x3f, sizeof f);
    f[1][1] = 0;
    
    for (int i = 2; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            for (int k = 1; k < i; k ++ )
                f[i][j] = min(f[i][j], f[k][j - 1] + (dist[i] - dist[k]) * speed[k]);
                
    int res = INF;
    for (int i = 0; i <= allow; i ++ ) res = min(res, f[n][n - i]);

    cout << res << endl;
}

signed main()
{
    //fast;
    T = 1;
    //cin >> T;
    
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

---

G - Hasan and his lazy students

G - Hasan and his lazy students

思路：

• 最长上升子序列求方案数

代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define fast ios::sync_with_stdio(false), cin.tie(nullptr); cout.tie(nullptr)

#define x first
#define y second
#define int long long

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-9;

const int N = 2010, M = N * 2;

const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int T, cases;
int n, m, allow;
int a[N];
int f[N];
int g[N];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )
        cin >> a[i];
    
    memset(f, 0, sizeof f);
    memset(g, 0, sizeof g);
    
    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for (int j = 1; j < i; j ++ )
            if(a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
        
        g[i] = 0;
        for (int j = 1; j < i; j ++ )
            if(a[j] < a[i] && f[i] == f[j] + 1)
                g[i] =(g[i] + g[j]) % mod;
        if(!g[i]) g[i] = 1;
    }
    
    int res = 0;
    for (int i = 1; i <= n; i ++ )  res = max(res, f[i]);
    
    int num = 0;
    for (int i = 1; i <= n; i ++ )
        if(f[i] == res) num = (num + g[i]) % mod;
    
    cout << res << " " << num << endl;
    
    return;
}

signed main()
{
    fast;
    T = 1;
    cin >> T;
    
    while(T -- )
        solve();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82