-
AVL树和2-3-4树详解
一、AVL树
BST存在的问题是,树在插入的时候会导致倾斜,不同的插入顺序会导致数的高度不一样,而树的高度直接影响了树的查找效率。最坏的情况所有的节点都在一条斜线上,这样树的高度为N。基于BST存在的问题,平衡查找二叉树(Balanced BST)产生了。平衡树的插入和删除的时候,会通过旋转操作将高度保持在LogN。其中两款具有代表性的平衡术分别为AVL树(高度平衡树,具备二叉搜索树的全部特性,而且左右子树高度差不超过1)和红黑树。
AVL树是如何实现平衡的呢?,具体是通过左旋或者右旋来实现的。具体如下图:
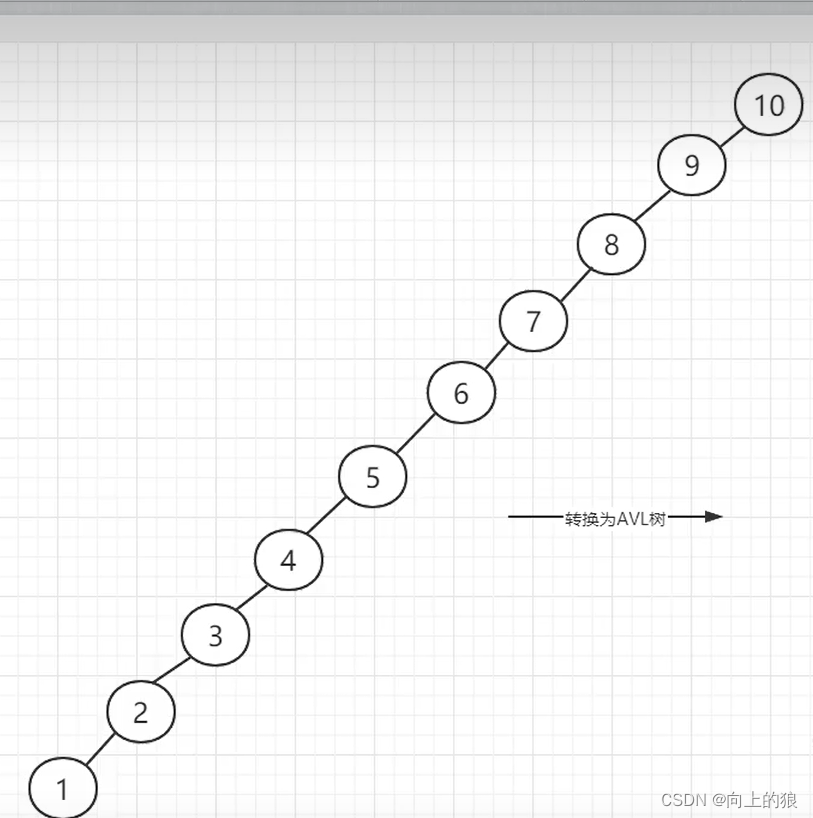
具体步骤:
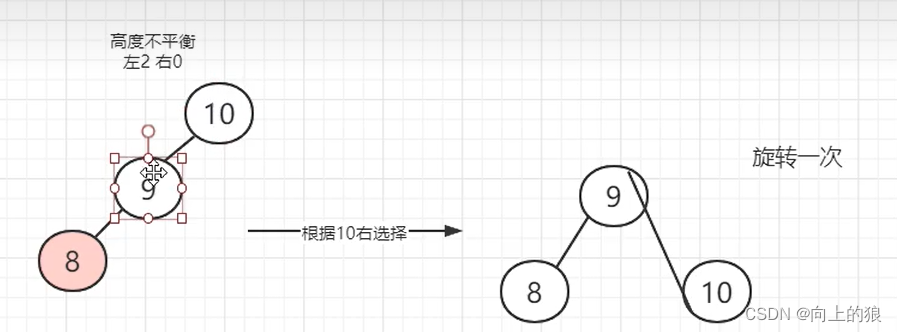
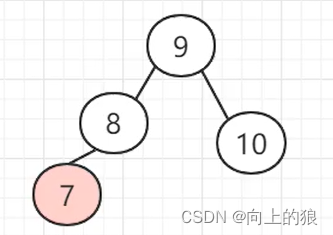
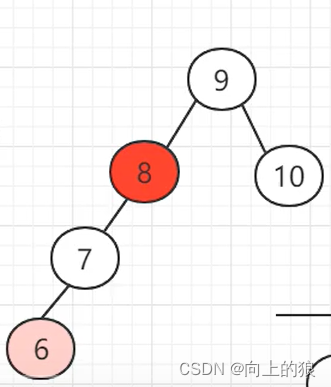
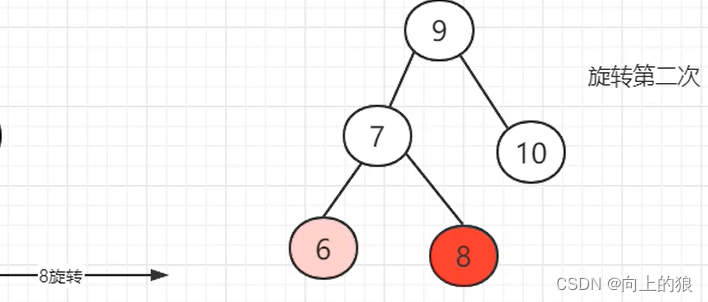
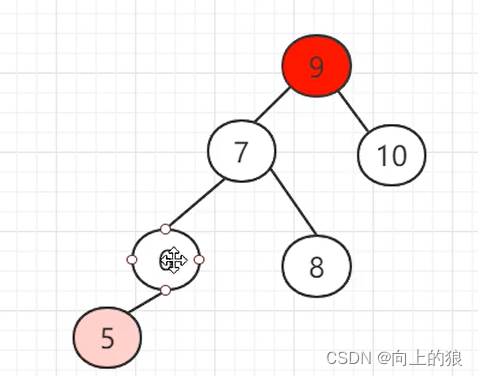
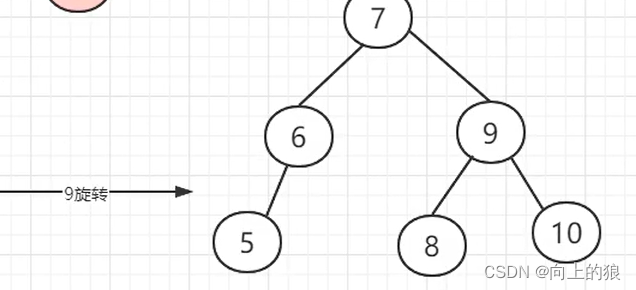
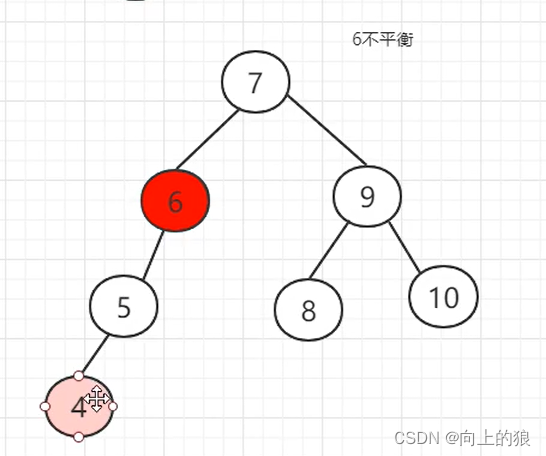
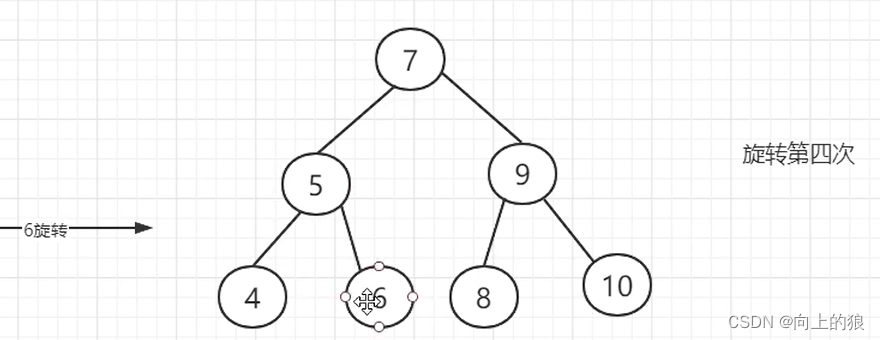
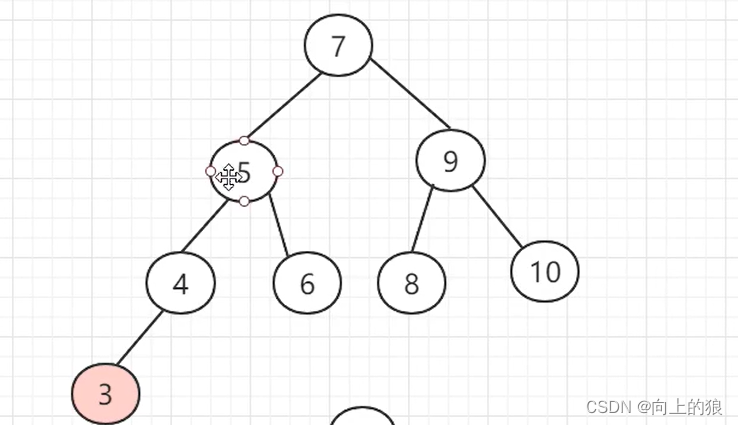
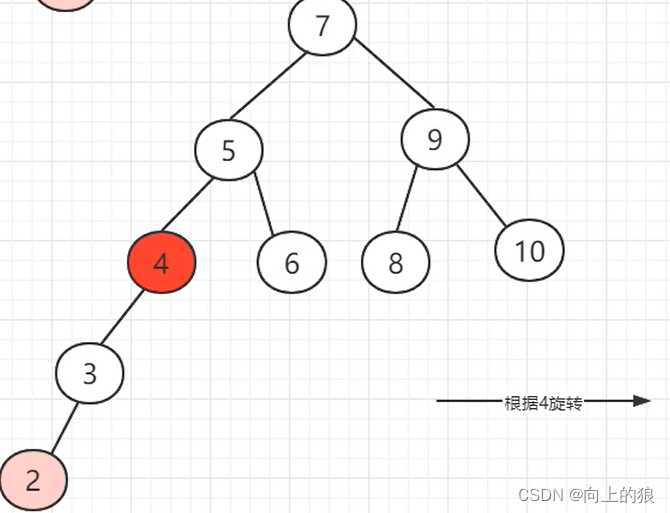
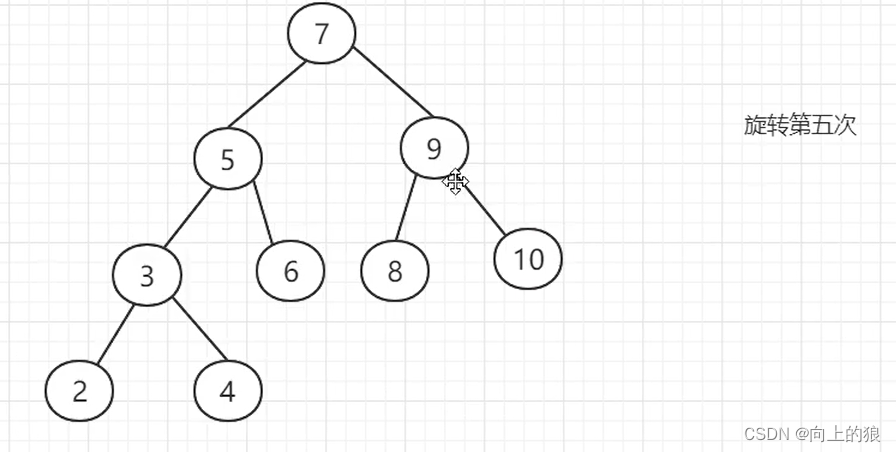
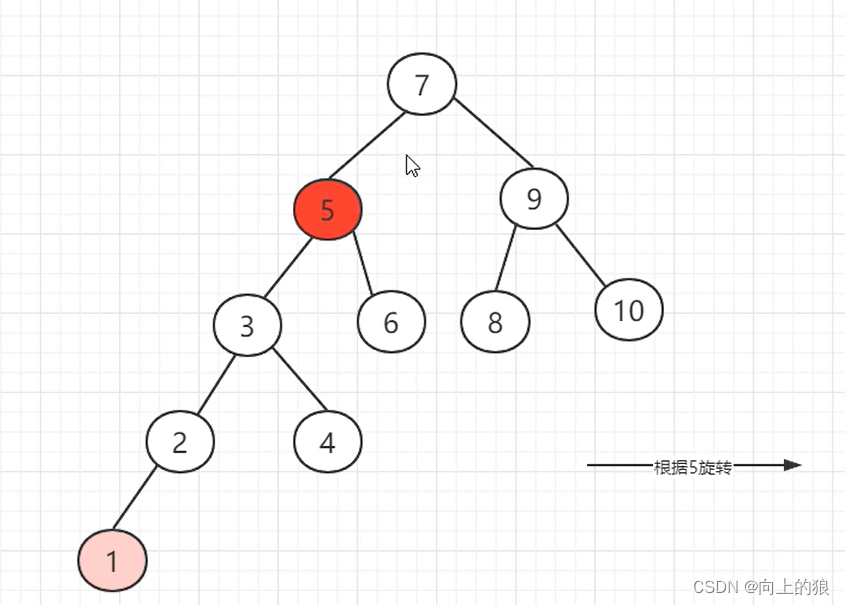
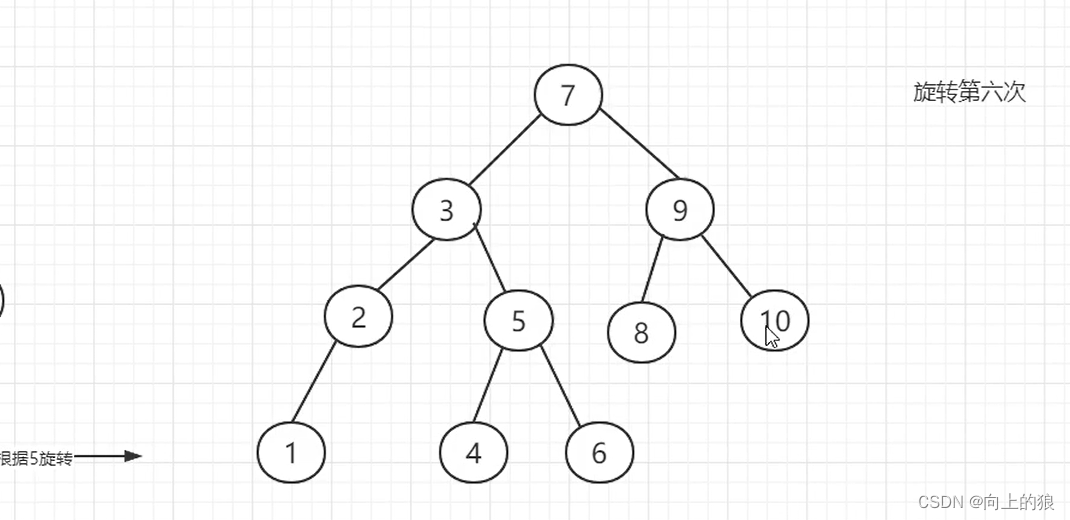
这就是将一个链表转换成AVL树的整个过程, 过程还是挺繁琐的, 主要就是通过左旋和右旋来实现.
二、2-3-4树
2.1、概念介绍
2-3-4树是四阶的B树(Balance Tree),他属于一种多路查找树,它的结构有以下限制:所有叶子节点都拥有相同的深度。
节点只能是2-节点、3-节点、4-节点之一。
- 2-节点:包含1个元素的节点,有2个子节点;
- 3-节点:包含2个元素的节点,有3个子节点;
- 4-节点:包含3个元素的节点,有4个子节点;
所有节点必须至少包含1个元素
元素始终保持排序顺序,整体上保持二叉查找树的性质,即父结点大于左子结点,小于右子结点;
而且结点有多个元素时,每个元素必须大于它左边的和它的左子树中元素。
下图是一个典型的2-3-4树
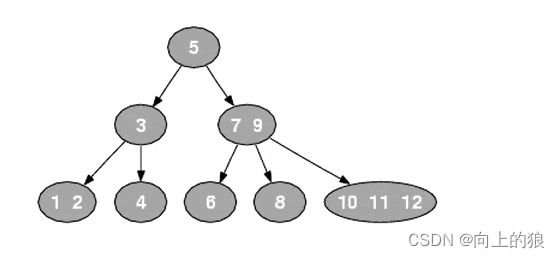
2-3-4树的查询操作像普通的二叉搜索树一样,非常简单,但由于其结点元素数不确定,在一些编程语言中实现起来并不方便,实现一般使用它的等同——红黑树。
2.2、生成的过程

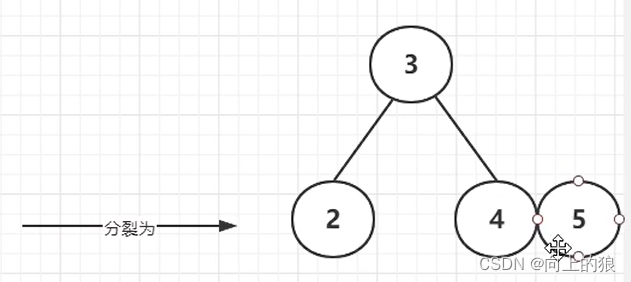
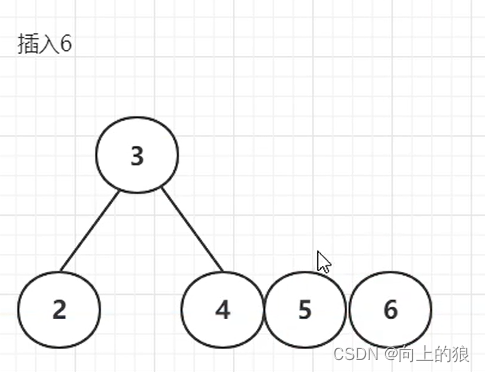
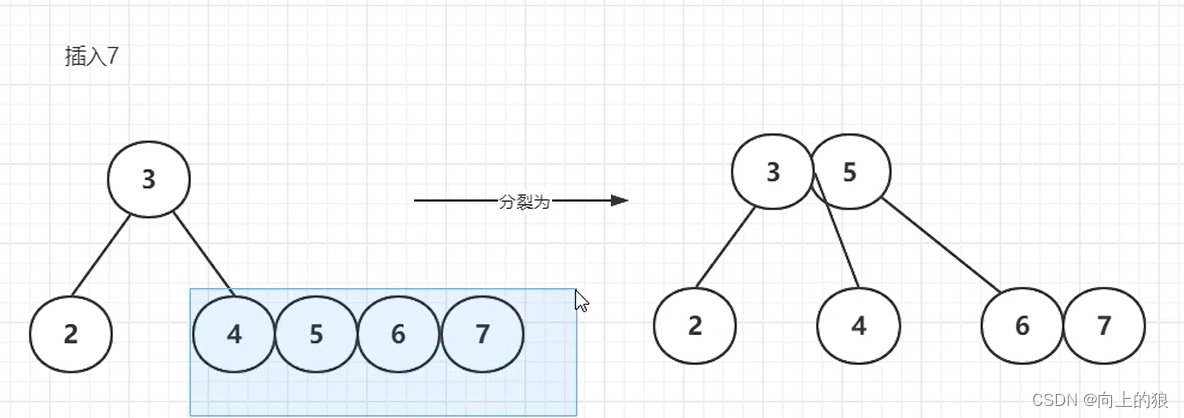
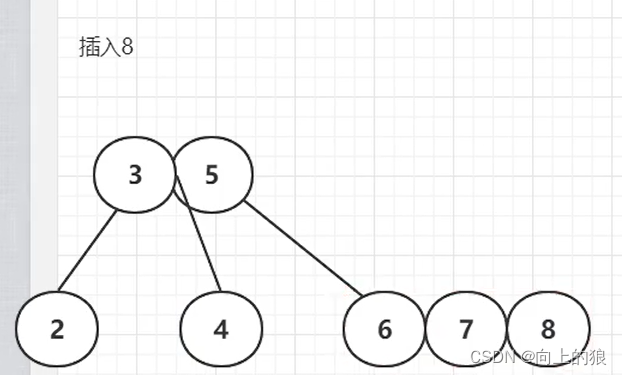
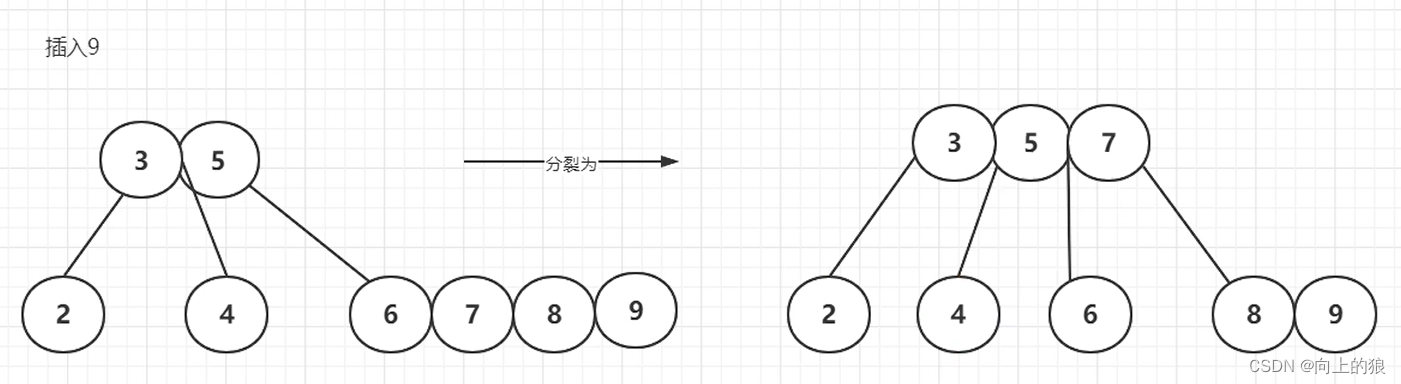


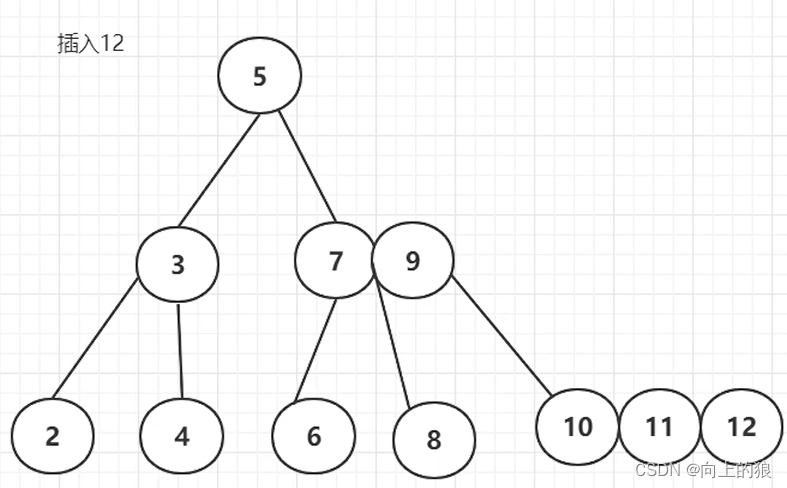
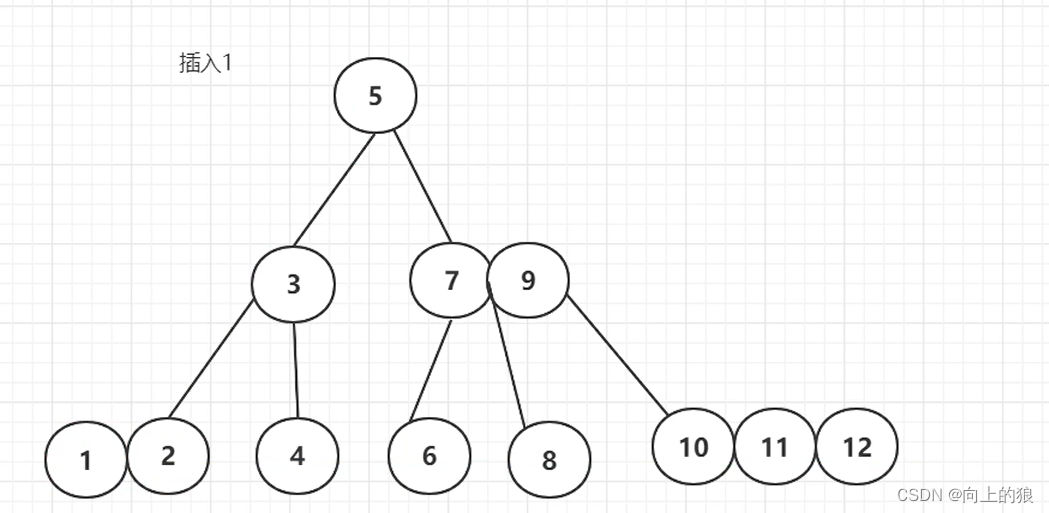
-
相关阅读:
7亿中国男人,今年夏天都在穿什么?
BGP数据包+工作过程
教育部:每所学校贷款项目总投资原则上不低于2000万
LeetCode每日一题(963. Minimum Area Rectangle II)
ARM hint instruction-WFI(Wait For Interrupt)指令详解
unity项目加密(比如到指定时间,项目打不开)
基于人工智能与边缘计算Aidlux的工业表面缺陷检测
Redis ----Spring MVC 有时候找不到类的原因
JavaScript基础
Matlab:绘制日期时间
- 原文地址:https://blog.csdn.net/m0_50370837/article/details/126498476