学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。 

学习日记

目录

​编辑

学习日记

一、前言

1、RNN概念

例

2、RNN用来干嘛 

二、RNN 

1、RNN的结构

2、RNN的多结构

one to one 

 one to n

 n-to-one

 n-to-n

---

一、前言

1、RNN概念

        RNN(Recurrent Neural Network)是一类用于处理序列数据的神经网络。那什么是序列数据呢？根据百度百科词条解释：时间序列数据是指在不同时间点上收集到的数据，这类数据反映了某一事物、现象等随时间的变化状态或程度。这是时间序列数据的定义，当然这里也可以不是时间，比如文字序列，但总归序列数据有一个特点——后面的数据跟前面的数据有关系。通俗理解就是一段连续的信息，前后信息之间是有关系地，必须将不同时刻的信息放在一起理解。比如一句话，虽然可以拆分成多个词语，但是需要将这些词语连起来理解才能得到一句话的意思。

        RNN是神经网络的一种，类似的我们会接触到的还有深度神经网络(DNN)，卷积神经网络(CNN)，生成对抗网络(GAN)等等。RNN的特点是对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息。我们可以利用RNN的这种能力，使深度学习模型在解决语音识别、语言模型、机器翻译以及时序分析等NLP领域的问题时有所突破。

例

        1、人类的自然语言，是不是符合某个逻辑或规则的字词拼凑排列起来的，这就是符合序列特性。如：我吃XXX，吃是一个动词，按照语法规则，那么它后面接名词的概率就比较大，在预测XXX是什么的时候就要考虑前面的动词吃的信息，如果没考虑上下文信息而预测XXX是一个动词的话，动词+动词，很大概率是不符合语言逻辑。

        2、我们发出的声音，每一帧每一帧的衔接起来，才凑成我们听到的话，这也具有序列特性。

        3、股票，随着时间的推移，会产生具有顺序的一系列数字，这些数字也是具有序列特性。

2、RNN用来干嘛 

        在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但这种普通的神经网络对于很多问题却无能无力。例，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNN之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。

        综上所述，可以得出RNN的一个特点：

                每一步的参数是共享的 

        理论上，RNN能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关。

二、RNN 

1、RNN的结构

        先看左半边图，如果不看隐藏层中的W，把它忽略，那么这其实就相当于是一个全连接神经网络的结构。那么从左图中就可以看出RNN其实只是相当于在全连接神经网络的隐藏层增加了一个循环的操作。至于这个循环的操作具体是怎样的？单看左图可能有些懵，那么现在看右图。右图是RNN网络结构按照时间线展开图。

Xt是t时刻的输入，是一个[x0,x1,x2…xn]的向量

U是输入层到隐藏层的权重矩阵

St是t时刻的隐藏层的值

W是上一时刻的隐藏层的值传入到下一时刻的隐藏层时的权重矩阵

V是隐藏层到输出层的权重矩阵

Ot是t时刻RNN网络的输出

        从右图中可以看出这个RNN网络在t时刻接受了输入Xt之后，隐藏层的值是St，输出的值是Ot。但是从结构图中我们可以发现St并不单单只是由Xt决定，还与t-1时刻的隐藏层的值St-1有关。

所谓的隐藏层的循环操作也就不难理解了，就是每一时刻计算一个隐藏层地值，然后再把该隐藏层地值传入到下一时刻，达到信息传递的目的。

具体隐藏层值St计算公式如下：

                                        S t = f ( U ⋅X t + W ⋅S t − 1 + b )

得到t时刻隐藏层的值后，再计算输出层的值：

                                        O t = g ( V ⋅ S t )

PS:在同一层隐藏层中，不同时刻的W，V，U均是相等地，这也就是RNN的参数共享。

2、RNN的多结构

one to one 

        最基本的单层网络，输入是x，经过变换Wx+b和激活函数f得到输出y。

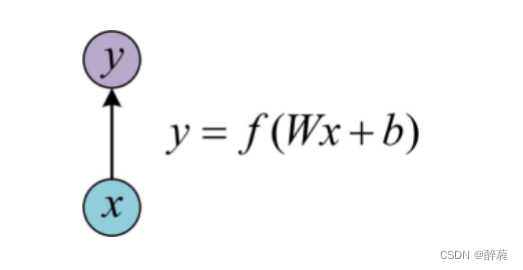
 one to n

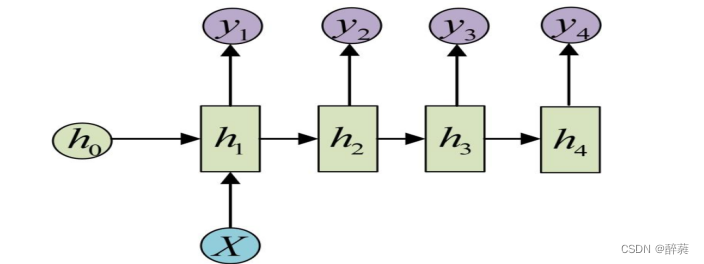
        还有一种结构是把输入信息X作为每个阶段的输入 

one-to-n 的结构可以处理的问题：从图像生成文字，从类别生成语音或音乐等

 n-to-one

        要处理的问题输入是一个序列，输出是一个单独的值而不是序列，只在最后一个h上进行输出变换就可以  。这种结构通常用来处理序列分类问题。      

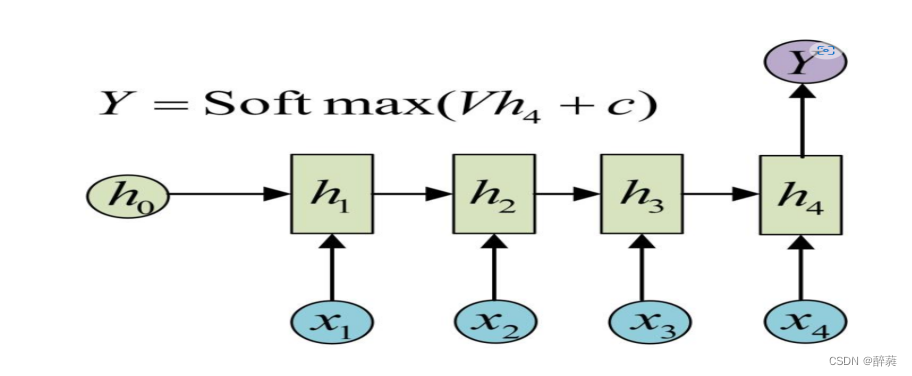
 n-to-n

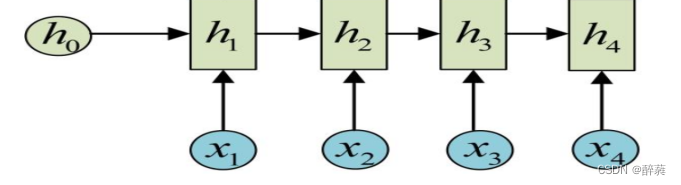
        最经典的RNN结构，输入、输出都是等长的序列数据。假设输入为X=(x1, x2, x3, x4)，每个x是一个单词的词向量。为了建模序列问题，RNN引入了隐状态h（hidden state）的概念，h可以对序列形的数据提取特征，接着再转换为输出。

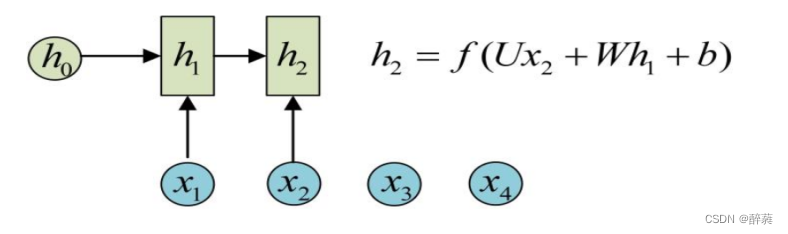
从h1的计算开始看

h2的计算 

依次计算

一个箭头就表示对对应的向量做一次类似于f(Wx+b)的变换，这里的这个箭头就表示对h1进行一次变换，得到输出y1。 

剩下的输出类似进行（使用和y1同样的参数V和c） 

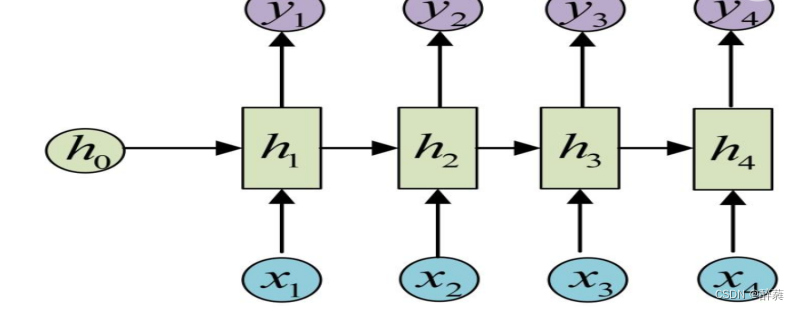
         这是最经典的RNN结构，它的输入是x1, x2, …..xn，输出为y1, y2, …yn，也就是说，输入和输出序列必须要是等长的。由于这个限制的存在，经典RNN的适用范围比较小，但也有一些问题适合用经典的RNN结构建模。