MATLAB程序设计与应用 3.5 稀疏矩阵

MATLAB程序设计与应用

3. 第3章 MATLAB矩阵处理

3.5 稀疏矩阵

所谓稀疏矩阵，是指具有大量零元素，而仅含极少量非零元素的矩阵。通常，一个mxn实矩阵需要占据m×n个存储单元，当m、n较大时，无疑要占据相当大的内存空间。然而，对稀疏矩阵来说，若将大量的零元素也存储起来，显然是对内存空间的浪费。为此，MATLAB为稀疏矩阵提供了方便灵活而有效的存储技术。

3.5.1 矩阵存储方式

MATLAB的矩阵有两种存储方式:完全存储方式和稀疏存储方式。

1. 完全存储方式

   完全存储方式是将矩阵的全部元素按列存储。之前用的矩阵的存储方式都是按这个方式存储的，此存储方式对稀疏矩阵也适用。不论是m×n普通矩阵还是稀疏矩阵均需要mXn个存储单元，而复矩阵还要翻倍。在这种方式下，矩阵中的全部零元素也必须输入。

2. 稀疏存储方式

   稀疏存储方式仅存储矩阵所有的非零元素的值及其位置，即行号和列号
   显然这对于具有大量零元素的稀疏矩阵来说是十分有效的。在MATLAB中，稀疏存储方式也是按列存储的。

   例如：

   

   A是具有稀疏特征的矩阵，其完全存储方式是按列存储全部12个元素:1、0、2、0、5、0、0、0、0、0、0、 7，其稀疏存储方式如下:

   (1,1),1,(3,1),2,(2,2),5,(3,4),7
   1

   括号内为元素的行列位置，其后面为元素值。上述矩阵A的稀疏存储方式也是占用12个元素空间，当原矩阵更加“稀疏”时,会有效地节省存储空间。

   注意，在讲稀疏矩阵时，有两个不同的概念，一是指矩阵的0元素较多，该矩阵是一个具有稀疏特征的矩阵;二是指采用稀疏方式存储的矩阵。

3.5.2 稀疏存储方式的产生

1. 将完全存储方式转化为稀疏存储方式

   函数A=sparse(S)将矩阵S转化为稀疏存储方式的矩阵A。当矩阵S是稀疏存储方式时，则函数调用相当于A=S。
   例子：

   >> X = [2,0,0,0,0; 0,0,0,0,0; 0,0,0,5,0; 0,1,0,0,-1; 0,0,0,0,-5];
   >> A = sparse(X)
   
   A =
   
      (1,1)        2
      (4,2)        1
      (3,4)        5
      (4,5)       -1
      (5,5)       -5
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10

   A 就是X 的稀疏存储方式。

   sparse函数还有其他一些调用格式。
   (1) sparse(m,n):生成一个mxn的所有元素都是0的稀疏矩阵。
   (2) sparse(u,v,S):其中u、v、S是3个等长的向量。S是要建立的稀疏矩阵的非零元素,u(i)、v(i)分别是S(i)的行和列下标，该函数建立一个max(u)行、max(v)列并以S为稀疏元素的稀疏矩阵。

   此外，还有一些和稀疏矩阵操作有关的函数。例如:
   (1)[u,v,S]=find(A):返回矩阵A中非零元素的下标和元素。这里产生的u、v、S可作为sparse(u,v,S)的参数。
   (2)full(A):返回和稀疏存储矩阵A对应的完全存储方式矩阵。

   示例：

   >> A = sparse([1,2,5,7],[1,3,2,3],[1,1,2,4])
   
   A =
   
      (1,1)        1
      (5,2)        2
      (2,3)        1
      (7,3)        4
   
   >> B = full(A)
   
   B =
   
        1     0     0
        0     0     1
        0     0     0
        0     0     0
        0     2     0
        0     0     0
        0     0     4
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20

2. 产生稀疏存储矩阵

   sparse 函数可以将一个完全存储方式的稀疏矩阵转化为稀疏存储方式矩阵，但在实际应用时，如果要创建一个大矩阵的稀疏存储方式矩阵,按照上述方法，则必须先建立该矩阵的完全存储方式矩阵，然后使用sparse函数进行转化，这显然是不可取的。能否只把要建立的稀疏矩阵的非零元素及其所在行和列的位置表示出来，然后由MATLAB直接产生其稀疏存储方式呢?这需要使用 spconvert函数，该函数将A所描述的一个稀疏矩阵转化为一个稀疏存储矩阵，调用格式: B = spconvert(A)

   其中，A为一个mx3或m×4的矩阵，其每行表示一个非零元素，m是非零元素的个数，A中每个元素的意义是，A(i,1)表示第i个非零元素所在的行，A(i,2)表示第主个非零元素所在的列，A(13)表示第i个非零元素值的实部，A(i,4)表示第i个非零元素值的虚部。若矩阵的全部元素都是实数，则无需第四列。
   该函数将A所描述的一个稀疏矩阵转化为一个稀疏存储矩阵。

   示例：根据表示稀疏矩阵的矩阵A，产生一个稀疏存储矩阵B。

   >> A = [2,2,1;3,1,-1;4,3,3;5,3,8;6,6,12];
   >> B = spconvert(A)
   
   B =
   
      (3,1)       -1
      (2,2)        1
      (4,3)        3
      (5,3)        8
      (6,6)       12
   
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11

   注意：矩阵A并非稀疏存储矩阵，只有B才是稀疏存储矩阵。

3. 带状稀疏存储矩阵

   用spdiags 函数产生带状稀疏存储方式矩阵。为便于理解，先看下列具有稀疏特征的带状矩阵。

   

   希望产生一个稀疏存储矩阵A。

   首先找出X矩阵的特征数据。包括矩阵的大小:5x6;有3条对角线，它们的位置与值依次为，第1条位于主对角线下方第3条，记d1=-3，该对角线元素值为0,0,0,41,51；第2条为主对角线，记d2=0，元素值为11、21、31、42、52；第3条位于主对角线上方第3条，记d3=3，元素值为12、22、32、0、0。于是，将带状对角线的值构成下列矩阵B，将带状的位置构成向量d：

   

   然后利用spdiags函数产生一个稀疏存储矩阵。

   >> B = [0,0,0,41,51;11,21,31,42,52;12,22,32,0,0]'
   
   B =
   
        0    11    12
        0    21    22
        0    31    32
       41    42     0
       51    52     0
   
   >> d = [-3,0,3]'
   
   d =
   
       -3
        0
        3
   
   >> A = spdiags(B , d , 5 , 6) % 产生一个稀疏存储矩阵A
   
   A =
   
      (1,1)       11
      (4,1)       41
      (2,2)       21
      (5,2)       51
      (3,3)       31
      (1,4)       12
      (4,4)       42
      (2,5)       22
      (5,5)       52
      (3,6)       32
   1
   2
   3
   4
   5
   6
   7
   8
   9
   10
   11
   12
   13
   14
   15
   16
   17
   18
   19
   20
   21
   22
   23
   24
   25
   26
   27
   28
   29
   30
   31
   32

   用spdiags函数产生带状稀疏矩阵的稀疏存储矩阵,调用格式如下：

   A=spdiags (B,d,m, n)
   其中，m、n为原带状矩阵的行数与列数。B为rxp矩阵，这里 r=min(m,n)，p为原带状矩阵所有非零对角线的条数，矩阵B的第i列即为原带状矩阵的第i条非零对角线。取值方法是，若非零对角线上元素个数等于r，则取全部元素；若非零对角线上元素个数小于r,则应该用零补足到r个元素。补零的原则是，当m

   spdiags函数的其他调用格式如下：
   (1) [B,d]=spdiags(A):从原带状矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线的位置向量d。
   (2) B=spdiags(A,d):从原带状矩阵A中提取由向量d所指定的那些非零对角线元素构成的矩阵B。
   (3) E=spdiags(B,d,A):在原带状矩阵A中将由向量d所指定的那些非零对角线元素用矩阵B替代，构成一个新的带状矩阵E。若赋值号左边改为A,则矩阵A为经过替换后的新稀疏矩阵。

4. 单位矩阵的稀疏存储

   单位矩阵只有对角线元素为1，其他元素都为0,是一种具有稀疏特征的矩阵。函数eye产生一个完全存储方式的单位矩阵。MATLAB还有一个产生稀疏存储方式的单位矩阵的函数，这就是speye。函数 speye(m,n)返回一个m×n的稀疏存储单位矩阵。

   >> s = speye(3,5)
   
   s =
   
      (1,1)        1
      (2,2)        1
      (3,3)        1
   1
   2
   3
   4
   5
   6
   7

3.5.3 稀疏矩阵应用举例

稀疏存储矩阵只是矩阵的存储方式不同，它的运算规则与普通矩阵是一样的。所以，在运算过程中，稀疏存储矩阵可以直接参与运算。当参与运算的对象不全是稀疏存储矩阵时，所得结果一般是完全存储形式。

>> A = [0,0,3;0,5,0;0,0,9]

A =

     0     0     3
     0     5     0
     0     0     9

>> B = sparse(A)

B =

   (2,2)        5
   (1,3)        3
   (3,3)        9

>> B * B  % 两个稀疏存储矩阵相乘，结果仍为稀疏矩阵

ans =

   (2,2)       25
   (1,3)       27
   (3,3)       81

>> rand(3) * B  % 普通矩阵与稀疏存储矩阵相乘，结果为完全存储普通矩阵

ans =

         0    4.7975    8.9074
         0    3.2787   11.1531
         0    0.1786    8.4852
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

案例：求下列三对角线性方程组的解。

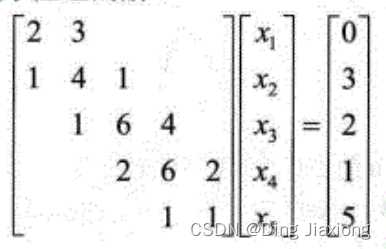
>> B = [1,2,0;1,4,3;2,6,1;1,6,4;0,1,2]; % 产生非0对角元素矩阵
>> d = [-1;0;1];    % 产生非0对角元素位置向量
>> A = spdiags(B , d , 5 ,5)  %产生稀疏存储的系数矩阵

A =

   (1,1)        2
   (2,1)        1
   (1,2)        3
   (2,2)        4
   (3,2)        1
   (2,3)        1
   (3,3)        6
   (4,3)        2
   (3,4)        4
   (4,4)        6
   (5,4)        1
   (4,5)        2
   (5,5)        1

>> f = [0;3;2;1;5]; % 方程右边参数向量
>> x = (inv(A) * f)' % 求解

x =

   -0.1667    0.1111    2.7222   -3.6111    8.6111
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

也可以采用完全存储方式来存储系数矩阵,结果如下:

>> A = full(A)

A =

     2     3     0     0     0
     1     4     1     0     0
     0     1     6     4     0
     0     0     2     6     2
     0     0     0     1     1

>> x = (inv(A) * f)' % 求解

x =

   -0.1667    0.1111    2.7222   -3.6111    8.6111
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

从本例可见，无论用完全存储还是用稀疏存储，所得到的线性代数方程组的解是一样的。