1. 　良好的特征

一个良好的特征，针对不同的问题需要有以下属性：

1. 具有信息量的；
2. 具有区分度的；
3. 独立的；

当前的使用方法：

数据　－－> 特征提取　－－> 　特征 －－> 　机器学习 －－>　预测 －－> 预测结果

1.1 　全局声学特征

全局特征的局限性在于，当信号是平稳信号才具有意义；
全局特征比如：　基频，　共振峰，　声强；

并且全局特征对噪声的鲁棒性较差，
由于实践过程中，经常处理非平稳信号，　所以对信号进行分帧，

将一小段信号，分成多个帧，　从而在每一帧当中，可以看做是平稳信号；

2. 　分帧

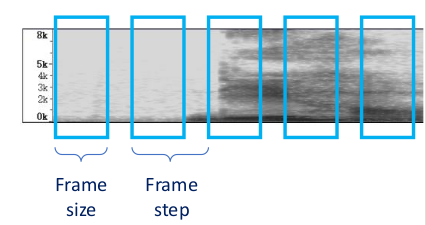
帧的大小：　决定了每一帧的持续时间；

帧移：　两个相邻帧，两帧的起始点之间间隔；

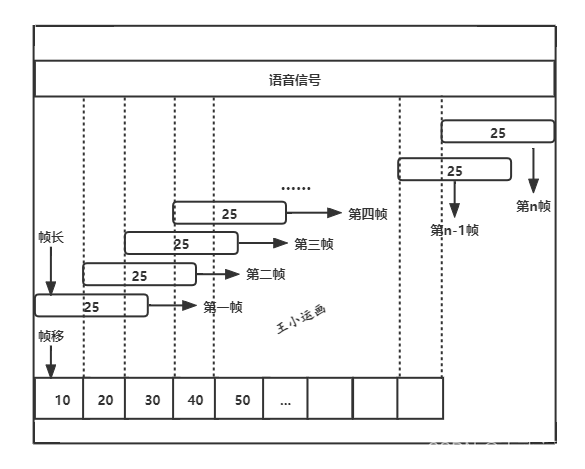
1. 当帧长大于帧移时：　帧之间有重叠的采样点，　属于绝大数情况；
2. 帧长　＝　帧移：　各帧之间相互独立；
3. 帧长　小于帧移：　各帧之间，存在采样点的丢失；

2.1 　以时间为单位进行分帧

当使用时间为单位，来对帧进行划分时：

一帧信号通常取在15ms-30ms之间，经验值为25ms(业界常用）。

帧长为25ms的一帧信号指的是时长有25毫秒的语音信号。

2.2 　以采样点数为单位进行分帧

用时间表示，常设为10ms；

用采样点表示，16kHz采样率的信号帧移一般为160个采样点。

3. 　分帧带来的影响

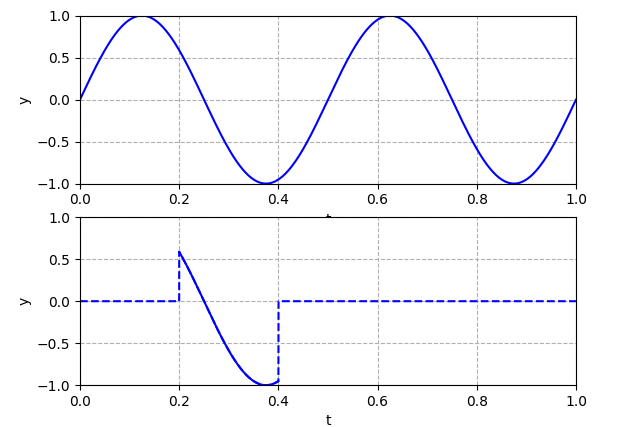
由于分帧之后的信号，　
在每一帧的起始点和终点的位置，有着高度的不连续性，　而原始的信号中则不存在这样的情况。

3.1 吉布斯现象

如果对分帧之后的信号，直接进行傅里叶变换，　则会产生吉布斯现象，在不连续点产生高频分量，导致傅里叶变换后的频谱出现局部峰值。

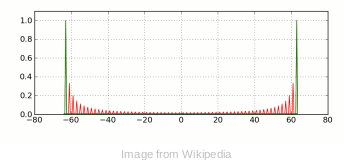
3.2 频谱泄露

周期信号在分帧中被截断，导致频谱在整个频带内发生拖尾现象，这个现象称为频谱泄露, spectral leakage;

为了去除哪些本不应该存在的高频分量，　以及频谱的拖尾现象，

产生了窗函数的方式；

4. 窗函数

窗函数的设计思想：

对帧内的每一个采样点，乘上不同的权重，
具体是，　使用较大的权重　乘以靠近窗中心的信号，
接近０的权重乘以　窗边缘的信号，

从而使得靠近帧中心的信号趋于原始数值，　分帧边界的信号趋于０；

4.1 　两种窗函数

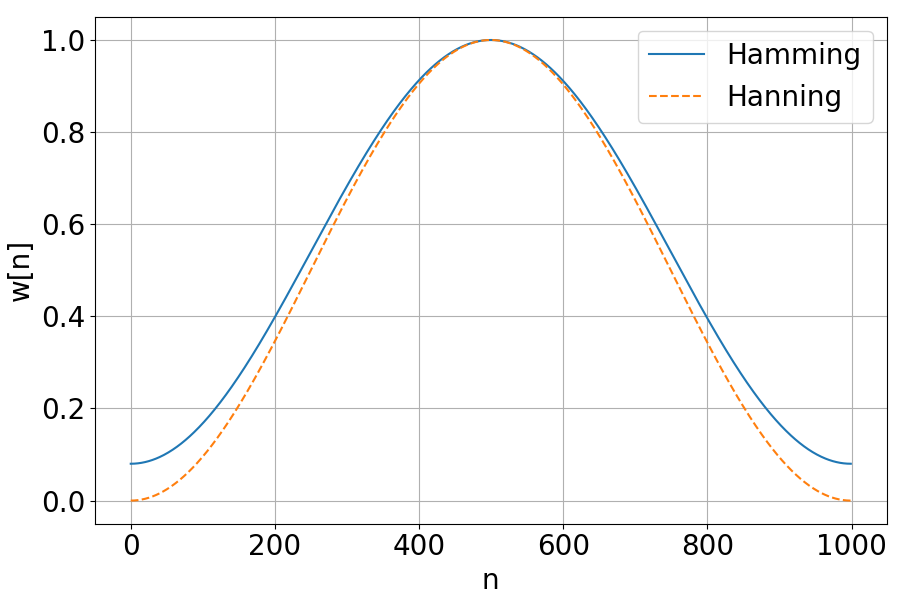
一帧内的采样点信号，　使用：
$x[n]$ , 0 ≤ n ≤ N − 1 表示；

窗函数的权重分布：
$$w[n]=(1-\alpha )-\alpha cos\frac{2\pi n}{N-1}$$

hanning 　与 hamming，两种窗函数之间的区别就是，　$\alpha$ 的取值系数不同；
• Hanning: α = 0.5
• Hamming: α = 0.46

5. 分帧特征的后处理

5.1 帧叠加

相邻两帧进行叠加，用于捕获更多的上下文信息；

5.2 帧的下采样

对相邻的两个叠加帧，　进行间隔采样；　从而减少计算量；

5.3 帧的归一化

对一帧内的数据进行归一化，　
从而有利于模型进行收敛；