力扣：11-盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

 

示例 1：

 

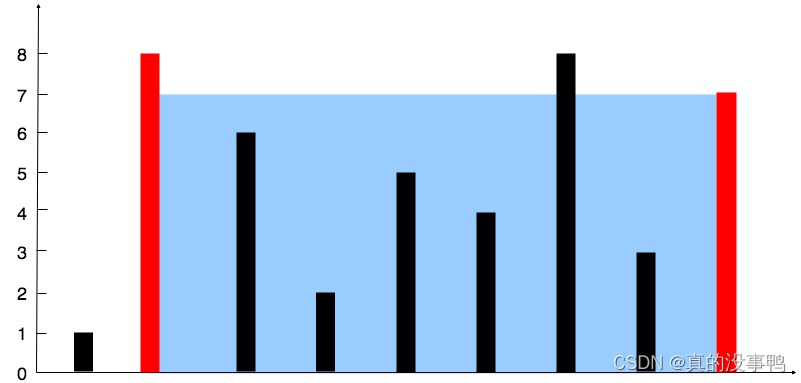
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1
 

提示：

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

来源：力扣（LeetCode）

解题思路

 这道题最优的做法是双指针做法，一开始雀氏不会往双指针方面想。首先的做法肯定就是暴力做法，两个for循环，但是两个for循环会超时，所以需要优化一下。最好的优化方法就是双指针算法。

由题目不难得出，容纳的水量是由两个点之间的距离乘上它俩中较小的height[i]，也就是：两个指针指向的数字中较小值∗指针之间的距离。双指针做法就是创建两个指针分别指向左右两端。然后我们需要考虑移动那个指针？应该移动对应height[i]较小的指针，为什么？因为两个指针是向内移动，所以指针之间的距离是越来越小，为了平衡这种减小，我们不可能移动指针指向的数字中的较大值的，因为这只会让差距越来越大。而移动较小值才是最稳妥的做法，虽然可能移动之后指针指向的值会更小，但也比移动较大值指针好一点。移动指向较大值的指针只会让结果变得更差。

这有点博弈论的味道，每次移动都只移动最差的一边，虽然可能会变差，但移动另外一个只会比这个更差。宁愿犯错，也不愿什么都不做。

代码实现

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i=0,j=height.size()-1;
        int ans=0;
        while(i
        {
            ans=max(ans,(j-i)*min(height[i],height[j]));
            if(height[i]
            i++;
            else
            j--;
        }
        return ans;
    }
};