图解LeetCode——782. 变为棋盘（难度：困难）

一、题目

一个 n * n 的二维网络 board 仅由 0 和 1 组成 。每次移动，你能任意交换两列或是两行的位置。

返回 将这个矩阵变为  “棋盘”  所需的最小移动次数 。如果不存在可行的变换，输出 -1。

“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。

二、示例

2.1> 示例 1:

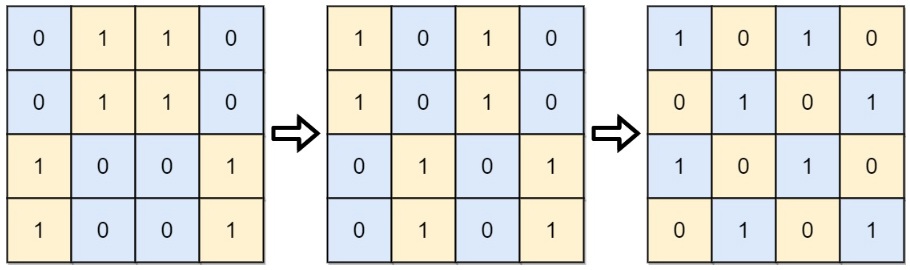
【输入】 board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
【输出】 2
【解释】一种可行的变换方式如下，从左到右：第一次移动交换了第一列和第二列。第二次移动交换了第二行和第三行。

2.2> 示例 2:

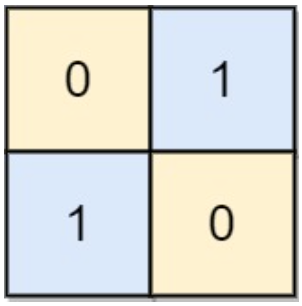
【输入】 board = [[0, 1], [1, 0]]
【输出】 0
【解释】 注意左上角的格值为0时也是合法的棋盘，也是合法的棋盘.

2.3> 示例 3:

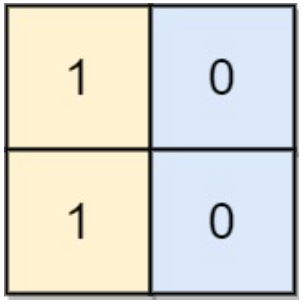
【输入】 board = [[1, 0], [1, 0]]
【输出】 -1
【解释】 任意的变换都不能使这个输入变为合法的棋盘。

提示：

• n == board.length
• n == board[i].length
• 2 <= n <= 30
• board[i][j] 将只包含 0或 1

三、解题思路

首先，根据题意，我们要计算出最小的可以变为“棋盘”的步数。那么，这道题的难度，其实就是如下两点：

难点1：如何判断出某个矩阵是否可以变为棋盘？
难点2：如何计算出变为棋盘的步数，并获得最小的步数作为方法的返回。

那么针对如上的难点，我们也一一的对其进行攻破。那么，首先，对于如何判断某个矩阵是否可以变为棋盘的问题，其实换句话说，就是，某个矩阵是否是本题约束下的“合法”矩阵。那么，既然要变化为棋盘，我们何不先将标准的棋盘结构分析一下，看看它们具有哪些特性。

3.1> 难点1：矩阵是否合法（判断条件一）

首先，针对于棋盘布局，其实也是分为两方面，分别为长度布局和数字布局：

长度布局：分为偶数（格子）长度和奇数（格子）长度。
数字布局：以0开始进行数字布局，还是以1作为数字布局。

那么，由于棋盘分为了长度布局和数字布局，那么就有如下四种情况的棋盘：

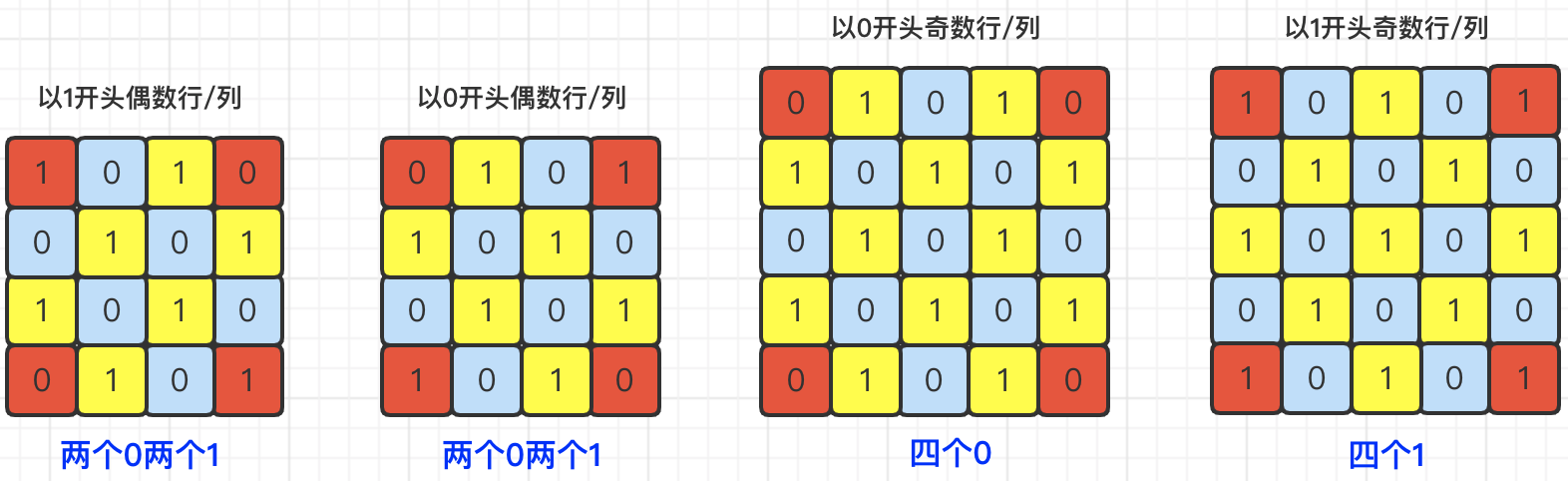
我们对其进行分析，发现对于红色标注的这四个“角”的格子，要么是四个0，要么是四个1，要么就是两个0和两个1。大家也可以通过移动上面的棋盘，会发现，无论如何移动，都会满足上述三种情况之一。那么，既然棋盘具有这种规律，我们在解题时，就可以首先通过判断上面的过滤，去过滤一批不合法的矩阵。

那么，我们怎么判断某一个矩阵是否满足上述三种条件呢？一种方法是，可以通过获取四个节点之后，通过if...else if 这种分支判断的方式，进行3种情况的判断。除了这种方式之外，其实，还有一种方式，就是通过按位异或来进行判断。因为按位异或的特点之一就是类似“翻牌”机制，如果两个数相同，则返回0，如果两个数不同，则返回1。那么，我们上面说的三种情况，0和1出现的次数只会是偶数次，那么，最终异或的结果也肯定为0。所以，我们反向判断一下，如果返回结果等于1，则说明是“非法”的矩阵，直接返回-1即可。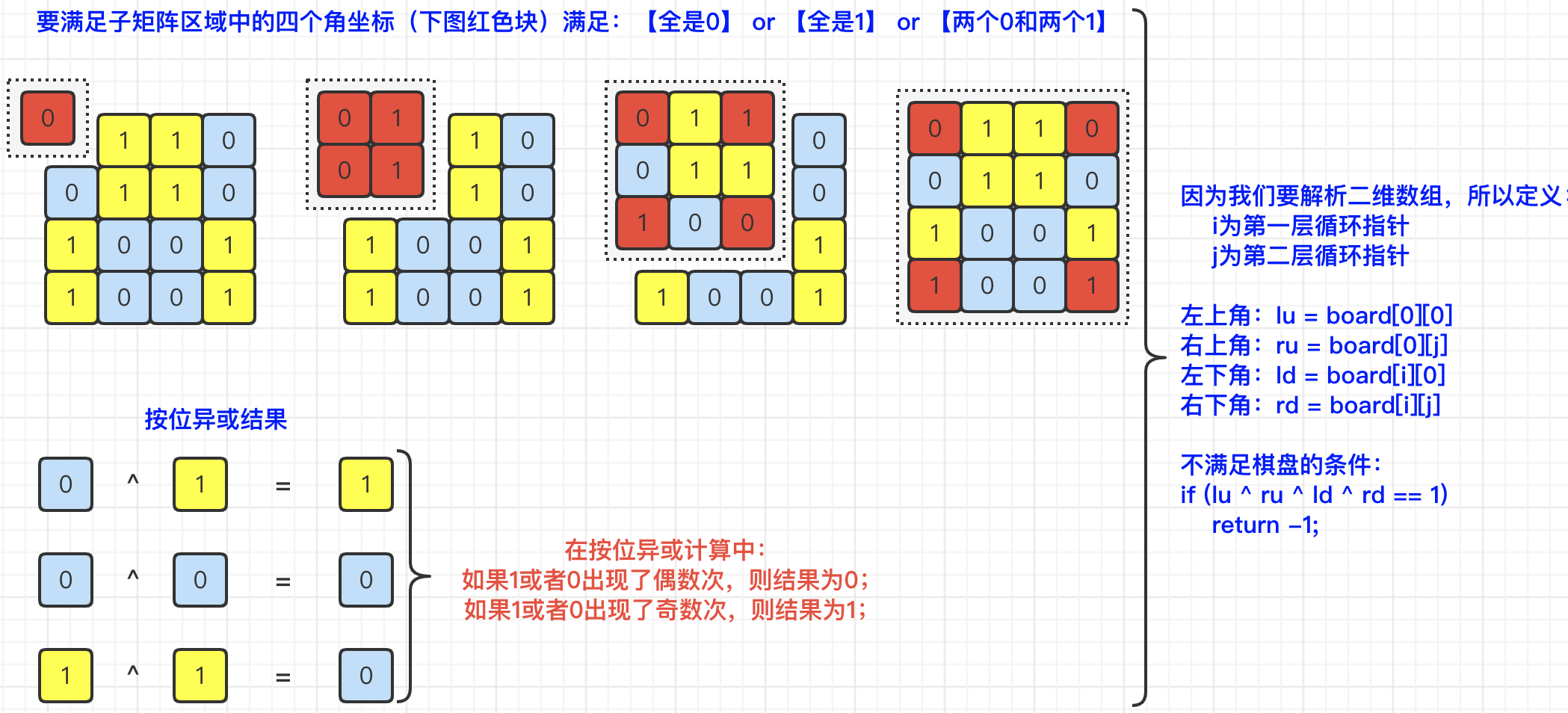

3.2> 难点1：矩阵是否合法（判断条件二）

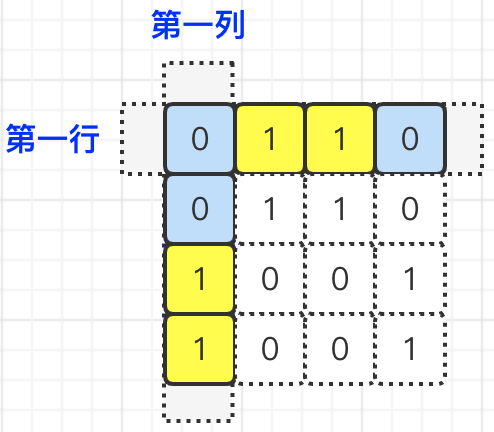
那么，由于棋盘中的每一行和列都是0与1互相穿插排序的，并且，虽然我们可以移动矩阵，但是我们改变的只是行或者列中元素的顺序，并无法改变它们的数量。那么，我们依然可以通过0和1出现的次数得出以下结论：

所以，通过上图我们可以发现，如果矩阵的长度为n，那么：

偶数行/列，1或0出现的次数就是：n/2。
奇数行/列，1或0出现的次数就是：n/2 或 (n+1)/2 。

如果某个矩阵不满足上述条件的话，那么则说明是非法矩阵，直接返回-1即可。

3.3> 难点2：如何计算出变为棋盘的步数

关于如何移动成为一个棋盘，因为我们是移动某一行或者某一列，那么只要这个矩阵满足了可以成为棋盘的条件之后，我们其实只需要关注第一行和第一列的移动情况即可。也就是说，第一行和第一列已经满足了棋盘的条件，其他行和列，必然也会满足棋盘的条件。

那么怎么移动矩阵称为棋盘，并且如何判断移动的步数呢？这里面，我们其实采用了“位差”的概念，也就是说，我们将矩阵的一行或者一列，去跟标准棋盘的一行或者一列进行对比（无论是以1开头还是以0开头，这个无所谓），他们之间出现的差值，其实就是我们应该移动的方格，而因为我们移动的时候，是任意的两行或者两列进行移动，那么每次移动，无论是针对行还是针对列，其实都是两个格子的变化，也就是说，(行的位差 + 列的位差)/2就是我们要移动的步数了。我们还是以下图为例，用图示的方式进行说明：

那么，在上面的图中，我们发现， 偶数行/列，会有偶数次格子的移动情况发生；如果是奇数行/列，会有偶数格子或奇数格子移动的情况发生。对于偶数位差，这个我们可以通过移动有位差的格子或者无位差的格子，这个都可以的。比如：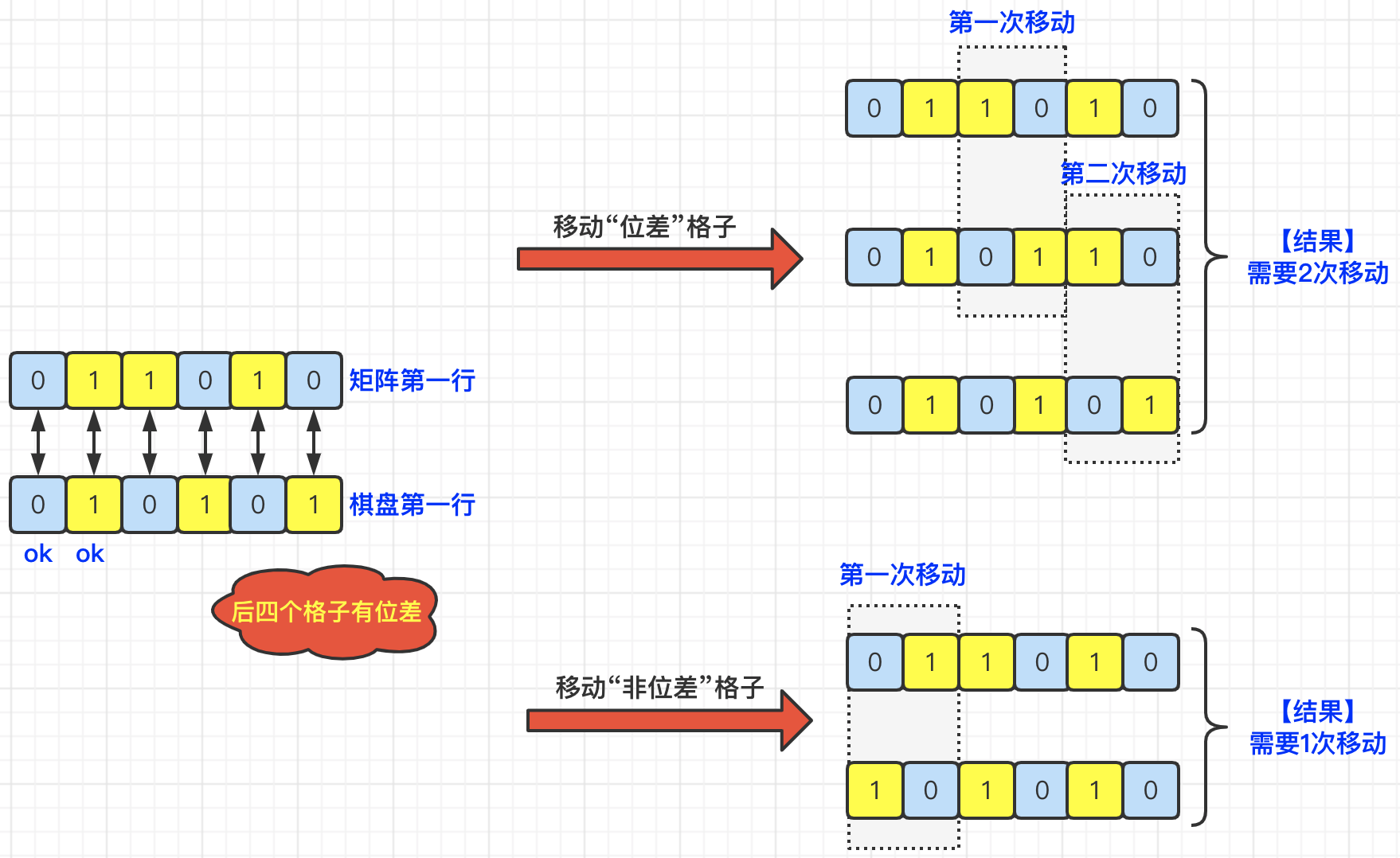

对于奇数位差，当我们计算出位差是奇数的时候，因为每次移动的都是偶数格子，所以，我们移动(n - 位差数)，如果是偶数位差，则跟上图一样。下图我们展示一下，当奇数位差时(n - 位差数)的示例：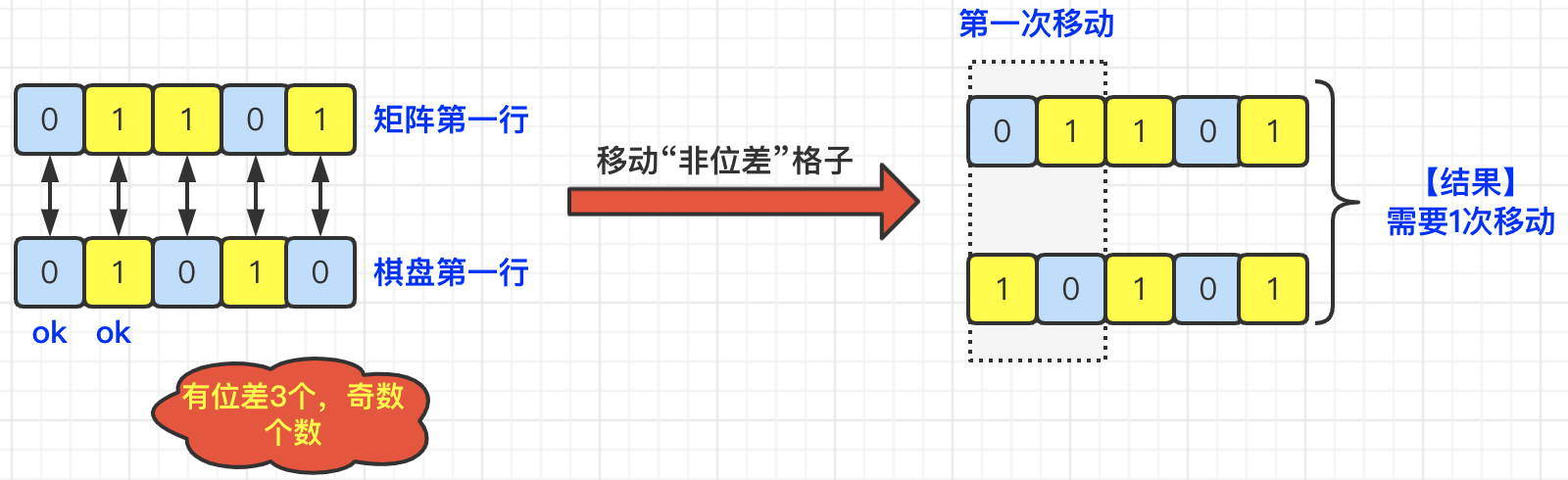

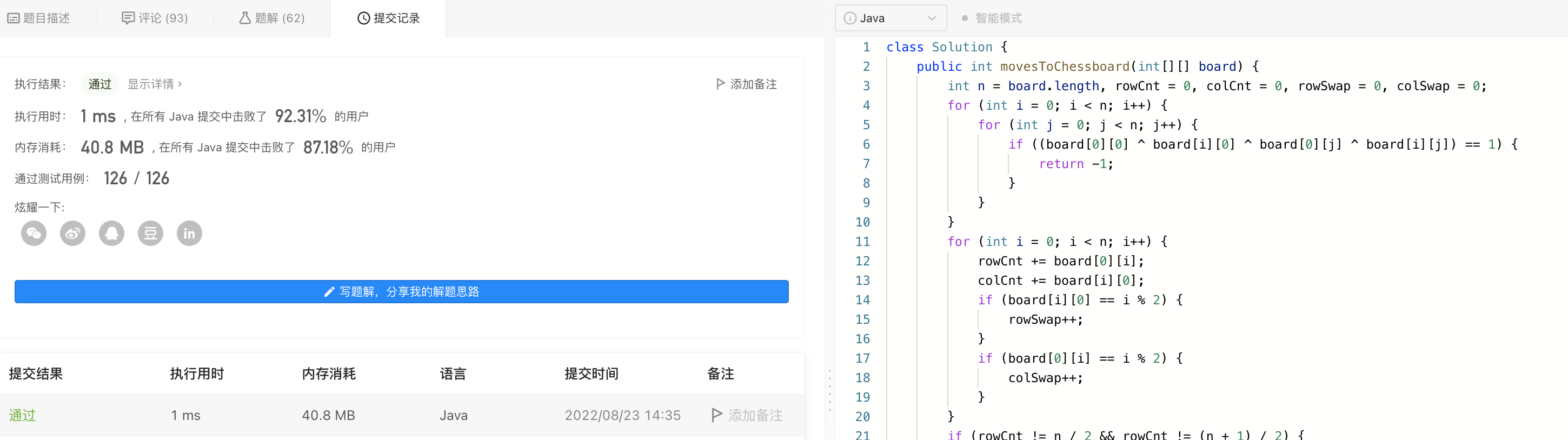
四、代码实现

由于本题我没有做出来，确实难度超出了我的能力范围了。我是参照Kvicii大佬的解题思路做的图解分析，文章的目的并不是显示我自己算法能力有多强，而是，希望能给一些同样对这道题没有思路的同学，一个更便于理解和学习的引路小短文。这里我就不班门弄斧了。将大佬的实现代码原样展示。

class Solution {
    public int movesToChessboard(int[][] board) {
        int n = board.length, rowCnt = 0, colCnt = 0, rowSwap = 0, colSwap = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if ((board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j]) == 1) {
                    return -1;
                }
            }
        }
        for (int i = 0; i < n; i++) {
            rowCnt += board[0][i];
            colCnt += board[i][0];
            if (board[i][0] == i % 2) {
                rowSwap++;
            }
            if (board[0][i] == i % 2) {
                colSwap++;
            }
        }
        if (rowCnt != n / 2 && rowCnt != (n + 1) / 2) {
            return -1;
        }
        if (colCnt != n / 2 && colCnt != (n + 1) / 2) {
            return -1;
        }
        if (n % 2 == 1) {
            if (rowSwap % 2 == 1) {
                rowSwap = n - rowSwap;
            }
            if (colSwap % 2 == 1) {
                colSwap = n - colSwap;
            }
        } else {
            rowSwap = Math.min(rowSwap, n - rowSwap);
            colSwap = Math.min(colSwap, n - colSwap);
        }
        return (rowSwap + colSwap) / 2;
    }
}

今天的文章内容就这些了：

写作不易，笔者几个小时甚至数天完成的一篇文章，只愿换来您几秒钟的 点赞 & 分享 。

更多技术干货，欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享，每天更新」