-
【快乐离散数学】命题逻辑 | 复合命题 | 等价命题 | Propositional Logic | Propositional Equivalences
WEEK1:Propositional Logic, Propositional Equivalences, Predicates and Quantifiers, Nested Quantifiers.

写在前面:本系列博客为复习离散的学习笔记,内容主要参考自 Kenneth Rosen 的 《Discrete Mathematics and Its Applications》和重庆大学刘然老师的《离散数学及其应用》课程。
🔗 视频教程:【重庆大学】《离散数学及其应用》刘然_哔哩哔哩_bilibili
目录
0x00 逻辑的概念(The concept of Mathematical Logic)
0x03 命题构造(Propositional construction)
* 0x04 Propositional Logic - Propositions
0x05 常用条件语句表述方式(Conditional Statements)
* 0x09 Logic and bit operations
Ⅲ. 等价命题(Propositional Equivalences)
0x00 等价命题(Propositional Equivalences)
0x01 非等价命题(Non-Propositional Equivalences)
0x02 逻辑运算符的优先级(Priority of logical operators)
Ⅳ. 命题逻辑的应用(Applications of Propositional Logic)
0x00 语句翻译(Translating sentences)
0x01 系统规范说明(System specifications)
O. 引言
0x00 离散数学的介绍
计算机开辟了脑力劳动机械化和自动化的新纪元,计算机的诞生,让你们就要为它进一步发展创建新的理论,就要寻找合适的数学工具。例如:为了描述新开拓的应用领域中的各种数据结构,就需要事宜的数学工具。
因为计算机系统从本质上来说是一种离散性的结构,计算机的许多性质得以在有限数学系统的框架中来理解,从中选出一些必要而且是基本的主干论题称为离散数学(Discrete mathematics)。因此,离散数学是随着计算机科学发展而逐步建立的,它形成于上世纪七十年代初期,是一门新兴的工具性学科:
"离散数学,构筑在数学与计算机之间的桥梁"
离散数学是现代数学的一个重要分支,是计算机科学与技术的理论基础,是计算机科学与技术专业的核心、骨干课程。它以研究离散量的结构和相互间的关系为主要目标,其研究对象一般是有限个或可数个元素,因此它充分描述了计算机科学离散型的特点。
0x01 世界的本质:连续 or 离散?
这个世界的本质是什么?是连续的还是离散的呢?当你学完离散数学你可能会感到:
"聚散皆是缘,离合总关情,一切皆离散。"
学习离散数学是为了学习计算机后继课程,如数据结构、编译原理、操作系统、数据库原理、形式语言及自动机、软件工程与方法学、计算机网络和人工智能、高级程序设计语言等,提供必要的数学基础,为阅读计算机文章作充分的数学准备。
0x02 注意事项
学习离散数学是比较困难的,在学习过程中可能会引发种种不良现象,如眩晕、恶心、头痛、出汗、甚至上吐下泻,这些都是正常现象,完全不用担心,因为这就是这门课的特点。

Ⅰ. 命题逻辑(Propositional Logic)
0x00 逻辑的概念(The concept of Mathematical Logic)
在讲解命题逻辑前我们首先要介绍一下什么是数理逻辑。
首先,罗技是电竞人必备的(划掉)📚 逻辑:是研究推理的科学。
逻辑起源于公元前四世纪,由希腊哲学家亚里士多德创建。它作为一门独立科学,其十七世纪德国的莱布尼兹给逻辑学引进了符号后,我们称之为数理逻辑(Mathematical Logic)。
🔍 类别:逻辑可分为 "形式逻辑" 和 "辨证逻辑" :
形式逻辑指的是通过数学方法(即引进一套符号体系的方法)从而变为数理逻辑的逻辑。
而辨证逻辑是以辩证法认识论的世界观为基础的逻辑学,就像马克思主义的唯物辩证法一样。
"物质世界是普遍联系和不断运动变化的统一整体"
- 形式逻辑是研究思维的形式结构和规律的科学,它撇开具体的、个别的思维内容,从形式结构方面研究概念、判断和推理机器正确联系的规律。
- 数理逻辑是用数学方法研究推理的形式结构和推理的规律的数学学科。它的创始人 Leibniz 为了实现把推理变为演算的想法,把数学引入了形式逻辑。其后,又经过多人努力,逐渐使数理逻辑称为一门专门的学课。
- 上个世纪 30 年代以后,数理逻辑进入一个崭新的发展阶段,逻辑学不仅与数学结合,还与计算机科学等密切关联了起来。
0x01 数理逻辑(Mathematical Logic)
数理逻辑又分为命题逻辑和谓词逻辑,我们本章主要探讨的是命题逻辑。
我们日常使用的自然语言,往往容易产生二义性。而计算机是最怕二义性的,计算机的执行永远都是确定的,即使是写随机函数,这个函数是怎么产生的也是要确定的。
比如下面这段话,我们读没什么问题,但计算机就是没法理解:
" 中国足球,谁也打不赢。中国乒乓球,谁也打不赢。"
这种模糊性的东西,我们就需要引入形式符号体系,在形式符号体系内包括命题。
0x02 命题(Propositional)
📚 定义:命题是一个陈述句(即陈述事实的语句),它或真或假,但不能既真既假。即:命题是能够判断真假的陈述句。
✅ 下面的陈述句均为命题:
(
 ) 月亮是绿色奶酪做的 # 异想天开
) 月亮是绿色奶酪做的 # 异想天开(
 ) 南京是安徽省的省会 # 当然是不是,玩笑话而已
) 南京是安徽省的省会 # 当然是不是,玩笑话而已(
 ) 东京是韩国的首都 # 显然错误
) 东京是韩国的首都 # 显然错误(
 ) 1 + 0 = 1 # 虽然是表达式,但是陈述了事实。1 + 0 确实等于 1
) 1 + 0 = 1 # 虽然是表达式,但是陈述了事实。1 + 0 确实等于 1(
 ) 0 + 0 = 2 # 不管是什么进制下这种都是错的
) 0 + 0 = 2 # 不管是什么进制下这种都是错的(
 )别的星球有生物 # 不知道有没有生物,但是用哲学思想思考一下,这个星球客观存在,它有没有生物我们虽然无法判断,但是它要么是真要么是假,不管你的认知水平有多高,它客观实在在那,所以是可以确定真假的,只是我们现在技术无法给一个客观的答案而已,所以我们还是认为它是个真命题。
)别的星球有生物 # 不知道有没有生物,但是用哲学思想思考一下,这个星球客观存在,它有没有生物我们虽然无法判断,但是它要么是真要么是假,不管你的认知水平有多高,它客观实在在那,所以是可以确定真假的,只是我们现在技术无法给一个客观的答案而已,所以我们还是认为它是个真命题。❌ 下面的语句均不是命题:
坐下! # 没有判断内容的感叹语句,不是命题
几点了? # 没有判断内容的疑问语句,不是命题
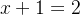 # 我真的不知道它是真假,如果取1是真,如果不取1就是假了
# 我真的不知道它是真假,如果取1是真,如果不取1就是假了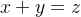 # 这个更什么都不知道了,无法判断真假
# 这个更什么都不知道了,无法判断真假我正在说谎 # 这是陈述句,但是看不出真假。假设我认为是 T,那我就真的在说谎,那真的我在说谎那这句话 "我正在说谎" 说的就是个假话了,我又得出 "我正在说谎" 是 F 的结论。如果我假设认为是 F,我不认同 "我正在说谎",是在说真话,那 "我正在说谎" 这句话就是真的了,我真的在说谎啊!那最后还是得到 T 的结论。我认为它是 T 的时候它是 F,我认为它是 F 的时候它是 T。所以这属于自指,这个我们后面讲,这种叫谬论(或称为悖论),这种就不能成为命题,因为仍然是没有办法判断真假的。
💡 说明:
① 只有具有确定真值的陈述句才是命题。一切没有判断内容的句子,无所是非的具体,如感叹语句、祈使句、疑问句等都不是命题。
② 因为命题只有两种真值,所以 "命题逻辑"(Propositional Logic) 又称为 "二值逻辑"(Binary Logic)。
③ "具有确定真值",是指客观上的具有,与我们是否知道它的真值是两码事。
0x03 命题构造(Propositional construction)
① 命题变元(Propositional argument):

② 一个命题是真命题用
 表示; 一个命题是假命题,用
表示; 一个命题是假命题,用  表示。
表示。③ 复合命题(Compound proposition):由原子命题用逻辑运算符组合而来:
- 否定联结词(Negation): ¬ not p
- 合取联结词(Conjunction):
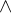 p and q
p and q - 析取联结词(Disjunction):
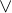 p or q
p or q - 条件联结词(Conditional):
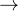
- 双条件联结词(Biconditional):
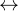

* 0x04 Propositional Logic - Propositions
proposition:命題
propositional variables:命題變元
Truth value:真值
Propositional calculus (logic):命題邏輯

Ⅱ. 复合命题(Compound Proposition)
0x00 否定联结词(Negation)
令
 为一命题,则
为一命题,则  记作 ¬
记作 ¬ ,读作 "非P" ,一元运算符。
,读作 "非P" ,一元运算符。 (取反)
(取反)① 如果
 表示 "地球是圆的"。则 ¬
表示 "地球是圆的"。则 ¬ 表示 "并非地球是圆的",也可以更简单地表示为 "地球不是圆的"。
表示 "并非地球是圆的",也可以更简单地表示为 "地球不是圆的"。② 如果
 表示 "咱们班上都是男同学",则 ¬
表示 "咱们班上都是男同学",则 ¬ 是表示 "咱们班上都不是男同学" 还是 "咱们班上不都是男同学" ?
是表示 "咱们班上都不是男同学" 还是 "咱们班上不都是男同学" ?按照建议是直接把 "不是或者非、并非" 放到句子前面去,即 "并非咱们班上都是男同学。"
0x01 合取联结词(Conjunction)
令
 和
和  为命题,
为命题, 、
、 的合取记作
的合取记作  。
。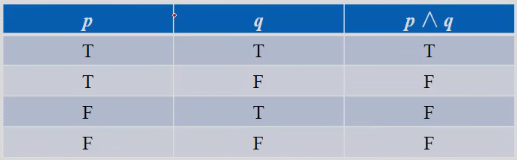 (按位与 & )
(按位与 & )当它们都为真时才为真,只要有一个是假就是假。
① 如果
 表示 "天在下雨",
表示 "天在下雨", 表示 "我在想你" 。则
表示 "我在想你" 。则 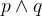 表示 "天在下雨并且我在想你"。
表示 "天在下雨并且我在想你"。《天在下雨我在想你》是任妙音的一首歌,只要
 、
、 是命题你就可以把它们合到一起。
是命题你就可以把它们合到一起。② 如果
 表示 "2月14日我在吃饭",
表示 "2月14日我在吃饭", 表示 "2月14日我女朋友在吃饭"。则
表示 "2月14日我女朋友在吃饭"。则 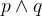 是表示 "2月14日我和女朋友在一起吃饭(原子命题)" 还是 "2月14日我和女朋友都在吃饭" 呢?答案是后者,这只能证明这一天我们两个都在吃饭,并不能说明我们两在这一天在一起吃饭。所以,不要看到一个 "和" 字就直接翻译成 "合取",这是错误的,要根据语言表达的意思来。
是表示 "2月14日我和女朋友在一起吃饭(原子命题)" 还是 "2月14日我和女朋友都在吃饭" 呢?答案是后者,这只能证明这一天我们两个都在吃饭,并不能说明我们两在这一天在一起吃饭。所以,不要看到一个 "和" 字就直接翻译成 "合取",这是错误的,要根据语言表达的意思来。0x02 析取连结词(Disjunction)
令
 和
和  为命题,
为命题, 、
、 的析取记作
的析取记作 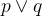 。
。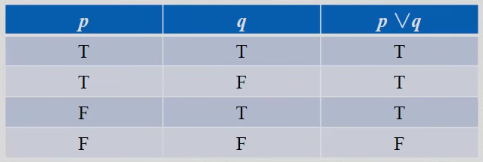 (按位或 | )
(按位或 | )只要其中有一个是真,就是真。两个都是假才是假。
如果
 表示 "天在下雨",
表示 "天在下雨", 表示 "我在想你" 。则
表示 "我在想你" 。则 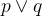 表示 "天在下雨或者我在想你"。
表示 "天在下雨或者我在想你"。0x03 条件联结词(Conditional)
"or" 有两种不同的含义:
① 兼或(inclusive or):在 "修过微积分或高数的学生可以修这门课" 这句话中,我们假设学生需要修期中一门必备课程,但可能两门都修了。这就是析取的含义。
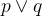 为真,只要两命题之一为真或两者均为真即可。
为真,只要两命题之一为真或两者均为真即可。② 异或(exclusive or):当我们去餐厅吃饭,看到 "套餐含可乐或橙汁" 时,往往是比较 sadly 的,这意味着我们并不能同时得到可乐和橙汁,而是要我们从中二选一,这就是异或(XOR)的含义。
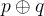 为真1,只要两命题之一为真,但不是两命题都为真。
为真1,只要两命题之一为真,但不是两命题都为真。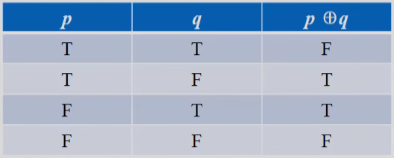 (按位异或 ^)
(按位异或 ^)异或异或,相同为假,不同为真。如果你觉得不太好记,这里介绍一种非常妙的判断方式:
💡 我们可以通过下面这句话去判断异或真假:
"他们是异性恋吗?"
额……虽然问起来怪怪的,但是真的好用!我们举几个例子你就能 Get 到有多妙了:
- 假设
 为
为  ,
, 为
为  ,他们是异性恋吗?NO,因为
,他们是异性恋吗?NO,因为 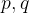 都为
都为  ,所以
,所以 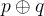 结果为
结果为  。
。 - 假设
 为
为  ,
, 为
为  ,他们是异性恋吗?YES,因为一个是
,他们是异性恋吗?YES,因为一个是  一个是
一个是  ,所以
,所以 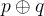 结果为
结果为  。
。 - 假设
 为
为  ,
, 为
为  ,他们是异性恋吗?NO,这和第一个例子一样,只是这次
,他们是异性恋吗?NO,这和第一个例子一样,只是这次 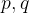 都是
都是  了,自然
了,自然 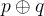 结果为
结果为  。
。
令
 和
和  是命题,则
是命题,则  是一个条件语句(或称为蕴含),implication (蘊含)
是一个条件语句(或称为蕴含),implication (蘊含)将其读作 " 如果
 ,则
,则  " 。 if p, then q.
" 。 if p, then q.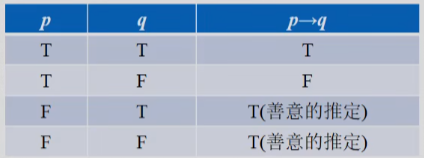
① 如果
 表示 "你安好",
表示 "你安好",  表示 "晴天"。则
表示 "晴天"。则  表示 "你若安好,便是晴天"。
表示 "你若安好,便是晴天"。② 在条件语句
 中,
中, 称为假设(前件、前提),
称为假设(前件、前提), 称为结论(后件)。
称为结论(后件)。如果前件为假,后件无论是
 还是
还是  ,我们都认为
,我们都认为  是
是  ,我们称之为 "善意的推定"。
,我们称之为 "善意的推定"。理解条件语句:
在条件语句
 中,前件和后件不需要有任何联系,
中,前件和后件不需要有任何联系, 只依赖于
只依赖于  和
和  的真值。
的真值。以下复合命题是真的,但在自然语言中没人会这么用,因为前后牛头不对马嘴:
"如果月亮是绿色奶酪做的,那么我比马斯克更有钱。" (
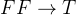 )
)"如果月亮是绿色奶酪做的,那么我就得靠劳保生活。" (前件是
 ,后件是什么不影响)
,后件是什么不影响)"如果
 ,那么猪会飞。"
,那么猪会飞。" (同上,前件是
 ,后件无论是
,后件无论是  还是
还是  都对结果没有影响,
都对结果没有影响, 为
为  。
。🔺 总结:前件与后件可以没有任何内在联系。
为了便于理解条件语句的真值表,可以将条件语句想象为合同或画饼。
- 如果我当选(
 ),那么我将会减税(
),那么我将会减税( )。
)。 - 我要有钱了(
 )我就给你分100万(
)我就给你分100万( )。
)。
如果这位政治家当选后没有减税,那么选民就可以说这家伙违背了竞选承诺。如果我有钱了但是没有给你100万,这不就是纯纯的画饼行为嘛,那么你就可以说我是在画饼。
0x05 常用条件语句表述方式(Conditional Statements)
A conditional statement is also called an implication (蘊含)

如果  则
则 
 条件
条件 
如果 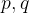
 仅当
仅当 
 除非 ¬
除非 ¬ 
 每当
每当 
 如果
如果 
 是
是  的充分条件
的充分条件 当
当 
 是
是  的必要条件
的必要条件 由
由  得出
得出 的必要条件是
的必要条件是 
 的充分条件是
的充分条件是 
0x06 逆命题、逆否命题与反命题
由条件语句
 可以构成一些新的条件语句:
可以构成一些新的条件语句: 是
是  的逆命题
的逆命题- ¬
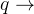 ¬
¬ 是
是  的逆否命题
的逆否命题 - ¬
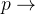 ¬
¬ 是
是  的反问题
的反问题
找出 "下雨我是不进城的充分条件" 的逆命题、逆否命题与反命题。
① 逆命题:如果我不进城,那就会下雨。
② 反命题:如果不下雨,我就进城。
③ 逆反命题:如果我不进城,那就不会下雨。
0x07 双条件联结词(Biconditional)
令
 和
和  为命题,则
为命题,则 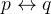 表示1双条件语句,
表示1双条件语句,称作 "
 当且仅当
当且仅当  " , "p if and only q", "p iff q"
" , "p if and only q", "p iff q" 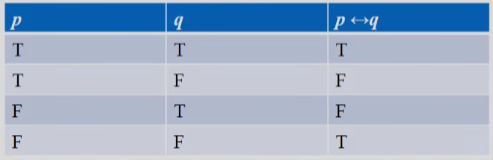 (同或)
(同或)如果
 表示 "我在家" ,
表示 "我在家" ,  表示 "天在下雨"。则
表示 "天在下雨"。则 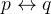 表示 "我在家当且仅当天在下雨" 。
表示 "我在家当且仅当天在下雨" 。同或同或,相同为真,不同为假。
💡 刚才我们讲了异或的巧妙判断方式,我们这也准备了判断同或真假的巧妙判断方式:
"他们是同性恋吗?"
- 假设
 为
为  ,
, 为
为  ,他们是同性恋吗?YES,因为
,他们是同性恋吗?YES,因为  都为
都为 ,所以
,所以  结果为
结果为  。
。 - 假设
 为
为  ,
, 为
为  ,他们是同性恋吗?YES,
,他们是同性恋吗?YES, 结果为
结果为  。
。 -
假设
 为
为  ,
, 为
为  ,他们是同性恋吗?NO,因为分别是
,他们是同性恋吗?NO,因为分别是  和
和  ,所以
,所以  为
为  。
。
双条件的表达方式(一切其他方式表达
 ):
): 是
是  的充分必要条件。
的充分必要条件。- 如果
 那么
那么  ,反之亦然。
,反之亦然。  当且仅当
当且仅当  。
。
0x08 真值表(Truth Table)
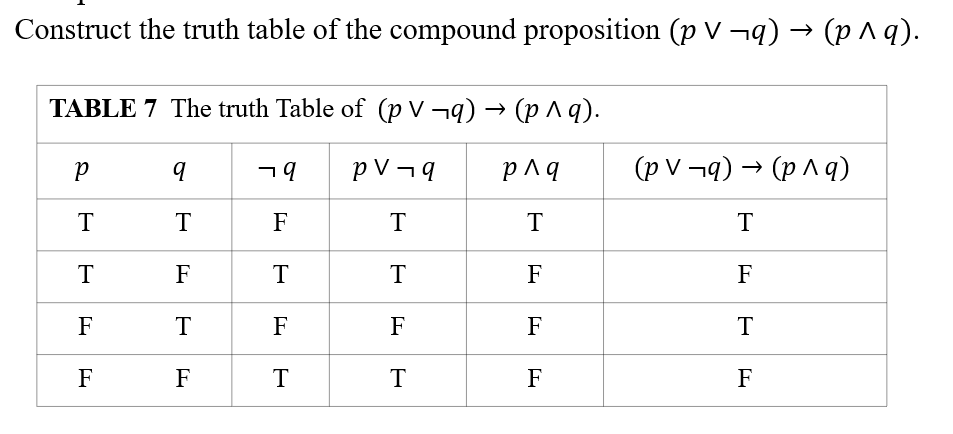
行(ROW):
- 原子命题的每个可能的值组合都需要一行。
列(COL):
- 复合命题需要一个列(通常在最右边)
- 需要一个列来表示在构建复合命题时出现的每个表达式的真值(这包括原子命题)。
试着构造复合命题
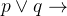 ¬
¬ 的真值表:
的真值表: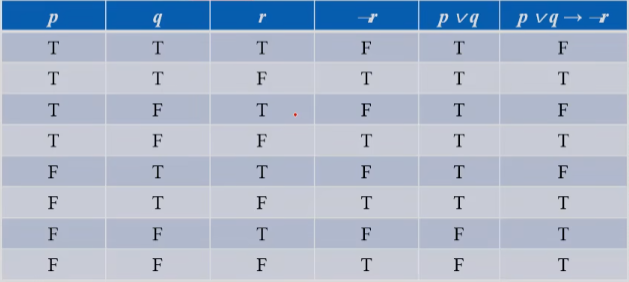
如果有三个变量,则有
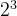 的组合,运算优先级:否定 > 析取 > 条件
的组合,运算优先级:否定 > 析取 > 条件 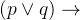 (¬
(¬ )
) * 0x09 Logic and bit operations
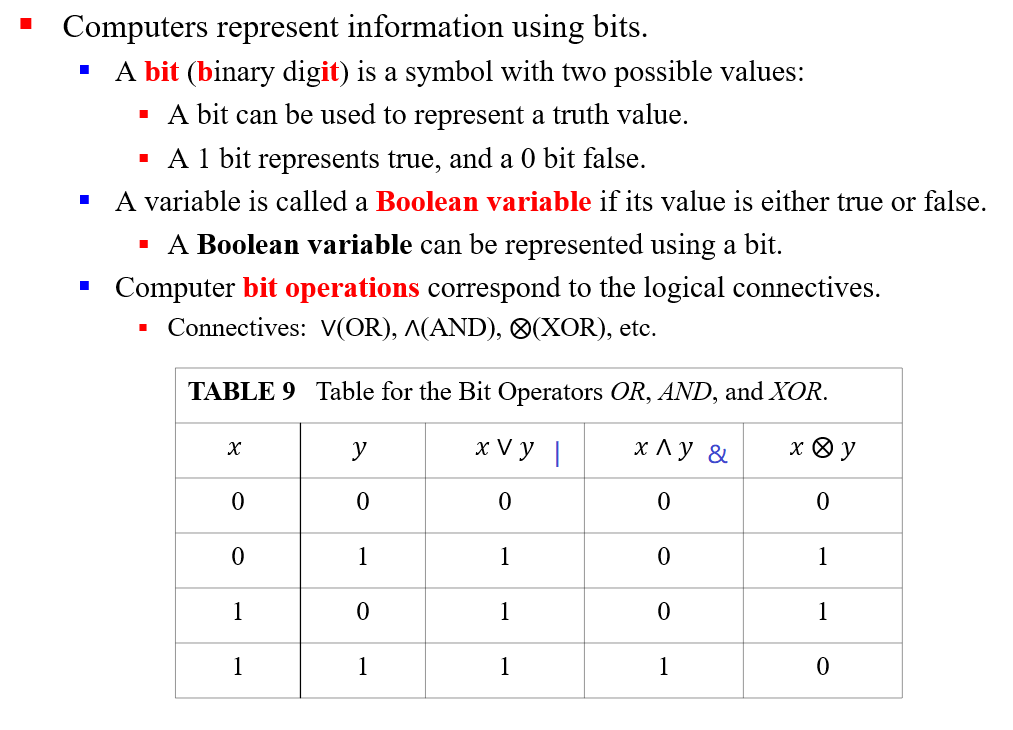 A bit string is a sequence of zero or more bits.
A bit string is a sequence of zero or more bits.The length of a bit string is the number of bits in the string.
Ⅲ. 等价命题(Propositional Equivalences)
0x00 等价命题(Propositional Equivalences)
如果两个命题总是有相同的真值,它们就是等价的。
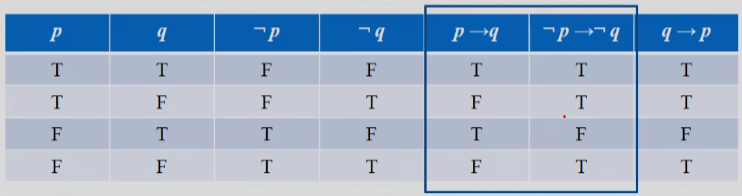
用真值表说明条件语句等价于逆否命题:
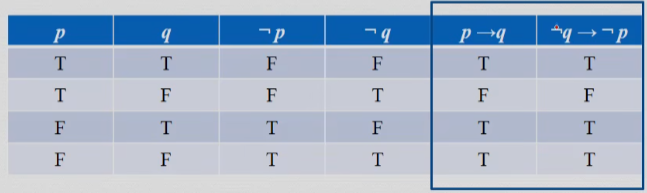
比如
 和 ¬
和 ¬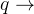 ¬
¬ 都是等价的,那么这就是个等价命题。
都是等价的,那么这就是个等价命题。① "
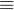 " 不是逻辑联结词。
" 不是逻辑联结词。② 命题公式之间逻辑相等关系具有:
- 自反性:
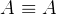 (自己跟自己总是等价的)
(自己跟自己总是等价的) - 对称性:若
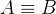 ,则
,则 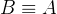 (如果我跟你等价,那你就跟我等价)
(如果我跟你等价,那你就跟我等价) - 传递性:若
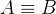 且
且 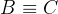 ,则
,则 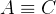 (我跟你等价并且你跟他等价,那么我跟他等价)
(我跟你等价并且你跟他等价,那么我跟他等价)
0x01 非等价命题(Non-Propositional Equivalences)
只要有一项不相同就是非等价命题:
❓ 问题:有
 个命题变元的真值表有多少行?
个命题变元的真值表有多少行?解:
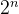
注意,这意味着有
 个命题变元,我们可以构造的不同的(即不相等)命题数量:
个命题变元,我们可以构造的不同的(即不相等)命题数量: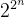
* 0x02 逻辑等价(Logical Equivalences)

0x02 逻辑运算符的优先级(Priority of logical operators)
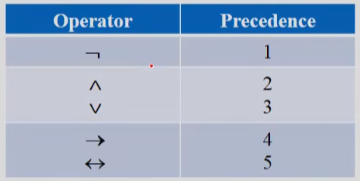 (否定是最高级)
(否定是最高级)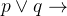 ¬
¬ 等价于
等价于 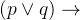 ¬
¬ ,这时候括号加不加其实无所谓。
,这时候括号加不加其实无所谓。但是如果它的本意是
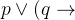 ¬
¬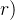 ,那么必须使用括号。
,那么必须使用括号。Ⅳ. 命题逻辑的应用(Applications of Propositional Logic)
0x00 语句翻译(Translating sentences)
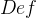 :命题演算的合成公式
:命题演算的合成公式 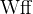 (Well formed formula),规定为:
(Well formed formula),规定为:① 单个命题变元本身是一个合式公式。
"单个命题变元是合式公式,单身狗是合法的"
② 如果
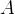 是合式公式,那么 ¬
是合式公式,那么 ¬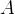 也是合式公式。
也是合式公式。"既然做单身狗是合法的,那么不做单身狗也是合法的"
③ 若
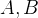 是合式公式,那么
是合式公式,那么 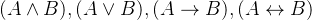 也是合式公式。
也是合式公式。"如果两个单身狗是合法的,那么他们之间合c'v取、析取、条件、双条件也都是合法的"
④ 当且仅当有限次地应用 (1)~(3) 所得到的包含命题变元、联结词和符号的括号串是合式公式。
"必须有限次的,你不能多次结婚多次离婚,这样是不行的"
将句子转换成命题逻辑语句的步骤:
- 识别原子命题并使用命题变元表示。
- 确定适当的逻辑连结词。
"如果我去汤姆家或乡下,我将不去购物"。
 :我去汤姆家
:我去汤姆家 :我去乡下
:我去乡下 :我将去购物
:我将去购物
则上述语句可以翻译为:
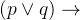 ¬
¬
if (res == p || res == q) return ~r;❓ 问题:请将下列句子翻译成命题逻辑
"只有你是计算机工学专业的学生,或者你不是新生,你才能在校园里上网。"
💡 分析:即,能在学校上网的前提是计算机工学的学生或不是新生。
解:设
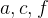 分别代表 "你能在校园里上网" ,"你是计算机工学专业的学生","你是新生"。
分别代表 "你能在校园里上网" ,"你是计算机工学专业的学生","你是新生"。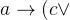 ¬
¬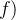

❓ 问题:重庆到北京的14次列车是下午5:30或者6:00开。
 :上海到北京的14次列车是下午5:30开;
:上海到北京的14次列车是下午5:30开; :上海到北京的14次列车是下午6:00开。
:上海到北京的14次列车是下午6:00开。💡 分析:这样的问题很符合常理,你问人车什么时候开,别人回答:"下午五点半或六点开吧",这肯定是没问题的,很自然。然而车不能开两次,不能五点半开一次六点又开一次,这肯定是做不到的。这就是不可兼,当表达或者的时候我们不能一贯的将其翻译成析取。
P 和 Q 相异时才对,所以应该取二三行。
❓ 问题:翻译下列句子
- (1)除非你努力,否则你将失败。
- (2)张三或者李四都可以做这件事。
💡 分析:(1)就相当于 "如果你不努力,你将会失败" 。(2)张三和李四都能做,要注意这个 "都",所以这里不翻译成 or,应该属于 and。张三和李四都可以做,应该是合取,而不是析取。
解:设 "你努力" 为
 ,失败为
,失败为  ,成功则为
,成功则为  ,则 ¬
,则 ¬ 。
。设张三能做事为
 ,李四能做事为
,李四能做事为  ,则
,则 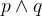 。
。0x01 系统规范说明(System specifications)
System specifications should be consistent.
系统和软件工程师根据自然语言描述的需求,生成精确而无二义性的规范说明,这些规范说明可作为系统开发的基础。
使用逻辑联结词表示规范说明:"当文件系统已满时,不能够发送自动应答"。
翻译这个规范说明的方法之一是:让
 表示 "能够发送自动应答",
表示 "能够发送自动应答", 表示 "文件系统已满"。
表示 "文件系统已满"。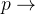 ¬
¬
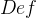 :如果为命题变量赋真值以使每个命题为真的情况成立,那么规范说明是一致的。
:如果为命题变量赋真值以使每个命题为真的情况成立,那么规范说明是一致的。下列规范说明是否一致?
- 诊断消息存储在缓冲区中或被重传
- 诊断消息没有存储在缓冲区中
- 如果诊断信息存储在缓冲区中,那么它被重传。
解:设
 表示 "诊断信息存储在缓冲区中",设
表示 "诊断信息存储在缓冲区中",设  表示 "诊断消息被重传",该规范说明可以写成:
表示 "诊断消息被重传",该规范说明可以写成: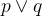 ,
, ,¬
,¬ 。当
。当  为假,
为假, 为真,这三个表述都为真,所以规格是一致的。
为真,这三个表述都为真,所以规格是一致的。如果 "诊断消息未被重传" 被添加上,他们还能保持一致吗?
解:现在我们把¬
 加上,有上上例推理可知,规范说明不一致。
加上,有上上例推理可知,规范说明不一致。0x02 布尔搜索(Boolean searches)
在搜索的过程中采用命题逻辑的技术,称为布尔搜索:
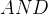 :用于匹配同时包含两个搜索项的记录
:用于匹配同时包含两个搜索项的记录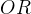 :用于匹配两个搜索项之一或两项均匹配的记录
:用于匹配两个搜索项之一或两项均匹配的记录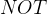 :用于排除某个特定的搜索项
:用于排除某个特定的搜索项

0x03 逻辑谜题(Logic Puzzles)
There are two kinds of inhabitants. Knights always tell the truth, and their opposites, knaves always lie. What are A and B if A says “B is a knight” and B says “The two of us are opposite types”?
一个岛屿上有两类人:骑士和骗子。
你去岛上碰见 A 和 B:
- A 说:"B是骑士"
- B 说:"我们两个不是同类人"
❓ 问题:A 和 B 的类型是什么?
解:设
 和
和  分别表示 A 是骑士,B 是骑士。则 ¬
分别表示 A 是骑士,B 是骑士。则 ¬ 表示命题 "A是个无赖",¬
表示命题 "A是个无赖",¬ 表示命题 "B是个无赖"。
表示命题 "B是个无赖"。- 如果 A 是骑士,那么
 是真的。既然骑士讲真话,
是真的。既然骑士讲真话, 也必须是真的。则
也必须是真的。则 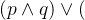 ¬p
¬p 必须是真的,但事实并非如此。所以 A 不是骑士, ¬p 必须是真的。
必须是真的,但事实并非如此。所以 A 不是骑士, ¬p 必须是真的。 - 如果 A 是个无赖,那么 B 一定不是骑士,因为无赖总是撒谎。所以 ¬
 和 ¬
和 ¬ 都成立,因为两者都是骗子。
都成立,因为两者都是骗子。
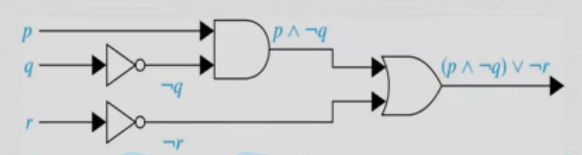
0x04 逻辑电路
📚 电路:每个输入 / 输入 可以被看作 0 或 1
- 0 代表 False
- 1 代表 True
复杂的电路是由三种简单的基本电路(也成为门电路)构成。

- 逆变器或 非门(NOT gate)接收一个输出位置并产生该位的否定。
- 或门(OR gate)接收两个输出位,并产生与这两个位的析取等价的值。
- 与门(AND gate)接收两个输出位,并产生与这两个为位的合取等价的值。
更复杂的数字电路可以通过将这些基本电路组合在一起产生给定输入信号的期望输出,方法是为每个输出表达式构建一个电路,然后将它们组合在一起。

- 📌 [ 笔者 ] 王亦优
- 📃 [ 更新 ] 2022.8.23
- ❌ [ 勘误 ] /* 暂无 */
- 📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
- 本人也很想知道这些错误,恳望读者批评指正!
📜 参考资料
Kenneth Rosen, Discrete Mathematics and Its Applications, 8th edition, McGraw-Hill
刘然老师. 重庆大学《离散数学及其应用》[EB/OL]. 2020.https://www.bilibili.com/video/BV1Hi4y1w7YA.
百度百科[EB/OL]. []. https://baike.baidu.com/.
-
相关阅读:
Hive 的权限管理
网络编程_sgu(620-635)
Python最强自动化神器Playwright!再也不用为爬虫逆向担忧了!
WMS类图结构分析-android12
信息学奥赛一本通:1107:校门外的树
网站一键灰色
验证码的编写
Mongo知识点整理
Linux下通过bonding技术实现网络负载均衡
我赢助手小技巧:学会这三招,爆款内容视频完播率提高50%(下)
- 原文地址:https://blog.csdn.net/weixin_50502862/article/details/126436351