二叉树相关OJ题目复习总结

最近开始复习了，疫情影响又要延迟开学，趁着这几天好好复习一下下，把二叉树的一些OJ题做做总结，权当练习代码能力，一个暑假数学建模培训占了好长时间，后面赶正式开学前抓紧复习吧！！！

二叉树中最近公共祖先https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/

 题目分析：

1、假设这棵树是双亲表示法（包含双亲的信息）——链表的思路

 求最近公共祖先，其实又是求两个链表的交点。

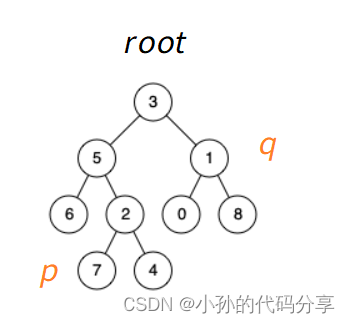
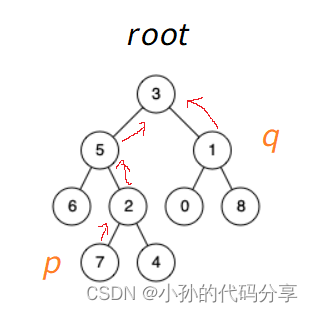
2、假设这棵树是二叉搜索树（排序树）_左子树比右子树小

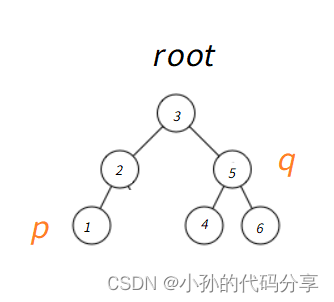
 求最近公共祖先

//1. 
p==root || q==root //此时最近公共祖先是root；
 
//2. 
p.val < root.val && q.val > root.val  || p.val > root.val && q.val < root.val
 
//  p在左            q在右                   p在右               q在左
 
//此时根节点root就是最近公共祖先；
 
//3.
p.val < root.val && q.val
 
//此时说明p和q都在root的左子树当中，此时需要递归到左子树上。
 
//4.
p.val > root.val && q.val > root.val
 
// 此时说明p和q都在root的右子树当中，此时需要递归到右子树上。

 

最终的代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return  null;
        }
        if(root == p || root == q){
            return root;
        }
        TreeNode retLeft = lowestCommonAncestor(root.left,p,q);
        TreeNode retRight = lowestCommonAncestor(root.right,p,q);
        if(retRight != null && retLeft != null){
            return root;
        }else if(retLeft != null){
            return retLeft;
        }else{
            return retRight;
        }
    }
}

3.申请两个栈空间来进行判断最近公共祖先（栈的思路）

先判断两个栈的大小，将大栈减到与小栈大小相等来进行 一 一比较，当相同时找到最近公共祖先。

栈思路的难点就是 如何找到 根节点 到 指定节点的路径，存到栈当中？

 该思路代码：

 

class Solution {
 
 
    public TreeNode lowestCommonAncestor(TreeNode root,TreeNode p, TreeNode q) {
        if(root == null || p == null || q == null) {
            return null;
        }
        Stack stack1 = new Stack<>();
        getPath(root,p,stack1);
 
        Stack stack2 = new Stack<>();
        getPath(root,q,stack2);
 
        int size1 = stack1.size();
        int size2 = stack2.size();
 
        if(size1 > size2) {
            int tmp = size1-size2;
            while (tmp != 0) {
                stack1.pop();
                tmp--;
            }
        }else {
            int tmp = size2-size1;
            while (tmp != 0) {
                stack2.pop();
                tmp--;
            }
        }
        //两个栈当中 元素的个数是一样的
        while (!stack1.empty() && !stack2.empty())  {
            if(stack1.peek() == stack2.peek()) {
                return stack1.peek();
            }else {
                stack1.pop();
                stack2.pop();
            }
        }
        return null;//没有公共祖先
    }
 
    /**
     * 找到根节点到指定节点node之间路径上的所有节点，存储到stack当中
     * @param root
     * @param node
     * @param stack
     */
    private boolean getPath(TreeNode root, TreeNode node,
                            Stack stack) {
        if(root == null || node == null) {
            return false;
        }
        stack.push(root);
        if(root == node) {
            return true;
        }
        boolean ret1 = getPath(root.left,node,stack);
        //不能判断false的问题，因为此时只能证明左边不存在
        if(ret1) {
            return true;
        }
        boolean ret2 = getPath(root.right,node,stack);
        if(ret2) {
            return true;
        }
        // 根节点不是  跟的左边没找到  根的右边没找到
        stack.pop();
        return false;
    }
}

二叉搜索树与双向链表https://www.nowcoder.com/practice/947f6eb80d944a84850b0538bf0ec3a5?tpId=13&&tqId=11179&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking

注意:

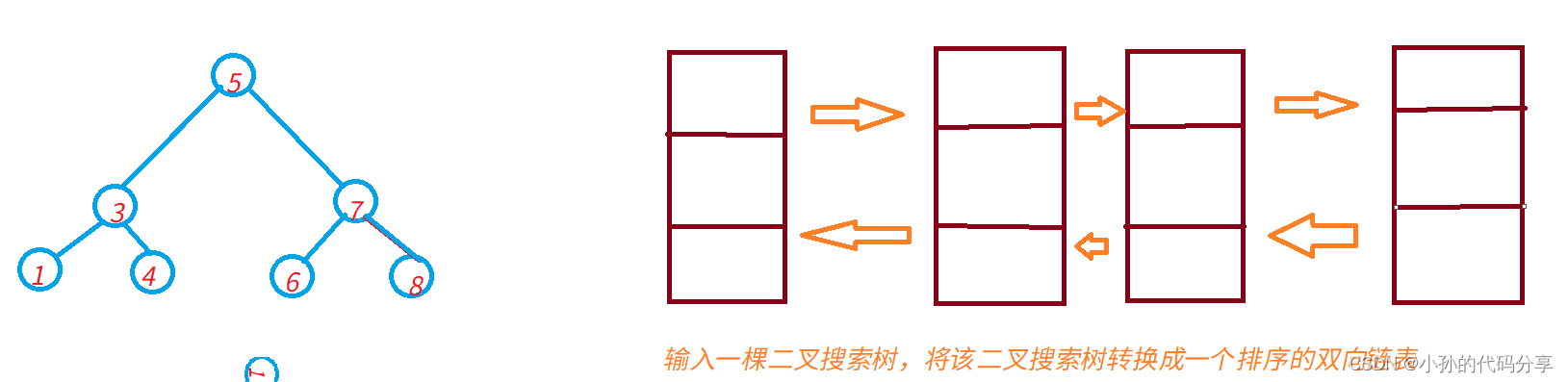
1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构

4.你不用输出双向链表，程序会根据你的返回值自动打印输出

输入描述：

二叉树的根节点

返回值描述：

双向链表的其中一个头节点

代码：

public class Solution {
    public TreeNode prev = null;
    public void ConvertChild(TreeNode root) {
        if(root == null) return;
        ConvertChild(root.left);
        //System.out.print(root.val+" ");
        root.left = prev;
        if(prev != null) {
            prev.right = root;
        }
        prev = root;
        ConvertChild(root.right);
    }
 
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree == null) return null;
 
        ConvertChild(pRootOfTree);
 
        TreeNode head = pRootOfTree;
        while(head.left != null) {
            head = head.left;
        }
        return head;
    }
}

从前序与中序遍历序列构造二叉树https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/ 

1.把前序遍历的值构建  根节点；

2.在中序遍历过程中找到  根节点的位置；

3.分别构建root的左树和右树

代码展示：

class Solution {
   public int preIndex = 0;
    private TreeNode buildTreeChild(int[] preorder,int[] inorder,int inbegin,int inend) {
        //没有了左树  或者 没有了右树
        if(inbegin > inend) {
            return null;
        }
        TreeNode root = new TreeNode( preorder[preIndex]);
        //找到当前根节点 在中序遍历中的位置
        int rootIndex = findInorderIndex(inorder, preorder[preIndex],inbegin,inend);
        preIndex++;
 
        root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);
 
        root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);
 
        return root;
 
    }
 
    private int findInorderIndex(int[] inorder,int val,int inbegin,int inend) {
        for(int i = inbegin;i <= inend;i++) {
            if(inorder[i] == val) {
                return i;
            }
        }
        return -1;
    }
 
    public TreeNode buildTree(int[] preorder, int[] inorder) {
 
        return buildTreeChild(preorder,inorder,0,inorder.length-1);
 
    }
}

从中序与后续遍历序列构造二叉树https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/submissions/

代码如下：

class Solution {
    
public int postIndex = 0;
 
    private TreeNode buildTreeChild(int[] postorder,int[] inorder,int inbegin,int inend) {
        //没有了左树  或者 没有了右树
        if(inbegin > inend) {
            return null;
        }
        TreeNode root = new TreeNode( postorder[postIndex]);
        //找到当前根节点 在中序遍历中的位置
        int rootIndex = findInorderIndex(inorder, postorder[postIndex],inbegin,inend);
        postIndex--;
        root.right = buildTreeChild(postorder,inorder,rootIndex+1,inend);
        root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1);
        return root;
    }
 
    private int findInorderIndex(int[] inorder,int val,int inbegin,int inend) {
        for(int i = inbegin;i <= inend;i++) {
            if(inorder[i] == val) {
                return i;
            }
        }
        return -1;
    }
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postIndex = postorder.length-1;
        return buildTreeChild(postorder,inorder,0,inorder.length-1);
    }
}

 根据二叉树创建字符串https://leetcode.cn/problems/construct-string-from-binary-tree/

 

 代码：

class Solution {
    public String tree2str(TreeNode root) {
        StringBuilder sb = new StringBuilder();
        tree2strChild(root,sb);
        return sb.toString();
    }
    private void tree2strChild(TreeNode root,StringBuilder sb){
        if(root == null) return;
        sb.append(root.val);
 
        if(root.left != null){
            sb.append("(");
            tree2strChild(root.left,sb);
            sb.append(")");
        }else{
            if(root.right == null){
                return;
            }else{
                sb.append("()");
            }
        }
        if(root.right == null){
            return;
        }else{
            sb.append("(");
            tree2strChild(root.right,sb);
            sb.append(")");
        }
    }
}