详解红黑树，图文并茂

前言

本文的相关概念和做法参考了《算法导论》和维基百科，有些图片也是来自维基百科的，下面贴上维基百科的链接，有兴趣的同学可以去看看。需要魔法才能上😉红黑树 - 维基百科，自由的百科全书 (wikipedia.org)，《算法导论》如果需要电子版可以私信我。

这篇文章的主要内容是红黑树的插入，没有删除。对于处理插入过程中的旋转如果没有了解，建议先去看我写的详解AVL树、图文并茂这篇博客，里面有平衡树旋转详细解释。

需要完整代码的，可以在我的Gitee仓库查看。数据结构/红黑树/RBTree.h (gitee.com)

一、红黑树

红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型用途是实现关联数组。它在1972年由鲁道夫·贝尔发明，被称为"对称二叉B树"，它现代的名字源于Leo J. Guibas和罗伯特·塞奇威克于1978年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在$O(lo{g}_{2}N)$时间内完成查找、插入和删除，这里的n是树中元素的数目。

红黑树是一颗二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是Red或者Black。同过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似于平衡的。

1.1 定义

树中每个节点的包含五个属性：color，left，right，parent和data。这里的left，right和parent都是节点类型的指针，构成的三叉链结构。

和AVL树是一样的。如果一个节点没有子节点或者父节点，则该节点相应属性的值为NIL。我们把这些NIL视为指向二叉搜索树的叶节点的指针(外部节点)，而把带关键字的节点视为树的内部节点。这个NIL在我们下面的讲述中没有多大作用，简单了解就行。

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

1. 节点是红色或黑色。
2. 根节点是黑色。
3. 所有叶子都是黑色(叶子是NIL节点)。
4. 每个红色节点必须有两个黑色的子节点。(或者说从每个叶子到根的所有路径上不能有两个连续的红色节点)
5. 从任一节点到其每个叶子(NIL)的所有简单路径都包含相同数目的黑色节点。

这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

要知道为什么这些性质确保了这个结果，注意到性质4导致了路径不能有两个连续的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

---

1.2 红黑树的节点定义

和AVL树是一样的三叉链结构，只不过把平衡因子换成了颜色。

enum Color { Red, Black }; // 使用枚举

template<class K, class V> 
// 红黑树节点
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	pair<K, V> _kv; // 这里存储的数据类型用的是pair
	Color _col;
	//节点构造函数
	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(Red) // 新节点的颜色默认为红色。 why？后面解释
	{}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

---

1.3 红黑树的定义

class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	RBTree()
		:_root(nullptr)
	{}
private:
    Node* _root;
}
1
2
3
4
5
6
7
8
9
10

---

二、操作

因为每一个红黑树也是一个特化的二叉查找树，因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而，在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的性质需要少量的颜色变更（实际是非常快速的）和不超过三次树旋转（对于插入操作是两次）。虽然插入和删除很复杂，但操作时间仍可以保持为$O(lo{g}_{2}N)$次。

---

2.1 插入

我们首先以二叉搜索树的方法增加节点并标记它为红色。下面要进行什么操作取决于其他临近节点的颜色。同人类的家族树中一样，我们将使用术语叔节点来指一个节点的父节点的兄弟节点。注意：

• 性质1和性质3总是保持着。
• 性质4只在增加红色节点、重绘黑色节点为红色，或做旋转时受到威胁。
• 性质5只在增加黑色节点、重绘红色节点为黑色，或做旋转时受到威胁。

如果新插入的节点不能为黑色呢？

如果设为黑色，就会导致根到叶子的路径上有一条路上，多一个额外的黑节点，这个是很难调整的。但是设为红色节点后，可能会导致出现两个连续红色节点的冲突，那么可以通过颜色调换（color flips）和树旋转来调整。

在插入过程中，会有两种插入情况，插入节点为红色，父节点为黑色或者红色。

1. 父节点为黑色。 不用处理
2. 父节点为红色。破环规则四(出现了连续的红节点)，需要调整。

---

2.1.1 寻找插入位置

和二叉搜索树，AVL树的是一样的，不再赘述。

bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_col = Black;
        return true;
    }
    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    //新增节点，颜色是红色，可能破坏规则4，产生连续的红色节点
    cur = new Node(kv);
    cur->_parent = parent;
    if (parent->_kv.first > kv.first)
        parent->_left = cur;
    else
        parent->_right = cur;

    //控制近似平衡
    //如果新增节点的父亲是红色，就需要继续处理
    //...
    
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

---

2.2.2 控制近似平衡和满足规则

我们先来分析分析破化规则的几种情况。在下面的示意图中，将要插入的节点标为cur，cur的父节点标为p，cur的祖父节点标为g，cur的叔节点标为u。

在插入后可以确定的是父节点一定是红，祖父节点一定是黑，而对于叔节点，是不知道情况的，所以下面的分析都是基于叔节点的：

1. cur为红，p为红，g为黑。u存在且为红。
2. cur为红，p为红，g为黑。u不存在或者u存在且为黑。
   • p和cur的子树方向一样，同为左子树或者同为右子树。 (例如 p是g的左子树且cur是p的左子树，或者同为右子树)
   • p和cur的子树方向不同，一个为左或者一个为右，或者相反。

---

1. 叔节点存在且为红

对于这种情况只需要简单的变颜色就可以。解决方式：将p和u改为黑，g改为红，然后将g改为cur，然后继续向上调整。

为什么g要由黑到红？

因为p和u变为黑，同路径上，为避免黑色节点增加，所以需要将g变为红。

为什么要继续向上调整呢？

这棵树可能只是局部的子树，在g的上面还有接节点，g的原本颜色是黑，所以g的父节点有可能为红，所以在g变色后，需要继续向上理。

---

2. 叔节点不存在或者存在且为黑

对于叔节点存在不存在的问题，这里先解释cur是不是新增节点的问题。

第一种情况，u不存在。cur为新增节点，就只是不满足连续红节点的问题，所以cur可以为新增节点。

对于第二种情况，u存在且为黑。cur作为新增节点好像是不合适的，因为如果没有新增节点时，这棵树就已经不满足每条路径上黑色节点数量相等了。所以cur一定不是新增节点。那么这种情况是怎么出现的呢？

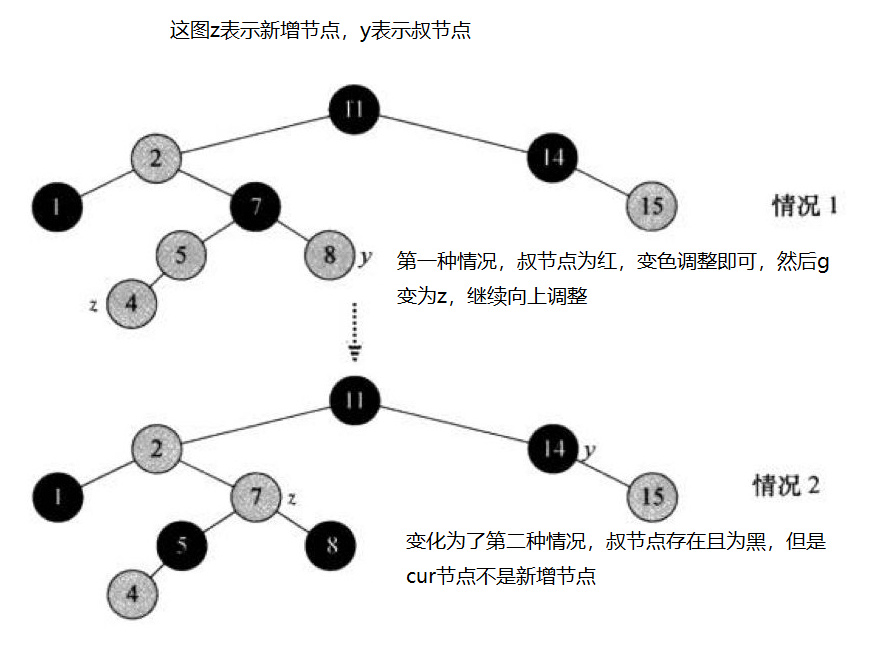
可以看出是由第一种情况变化出来的，情况的来源解释完了，现在来看怎么解决。这里对于u不存在可以整合为一种情况，只要考虑，左右子树的关系。

---

2.1 p和cur同为左子树或者右子树

下面图示只描述同为左子树，右子树是对称的，且变色处理是一样的。

p为g的左孩子，cur为g的左孩子，则进行右单旋。相反，p为g的右孩子，cur为p的右孩子，进行左单旋。然后p和g变色 – p变黑，g变红。这样就可以处理完毕，直接结束，不用像情况一一样，去继续调整。

---

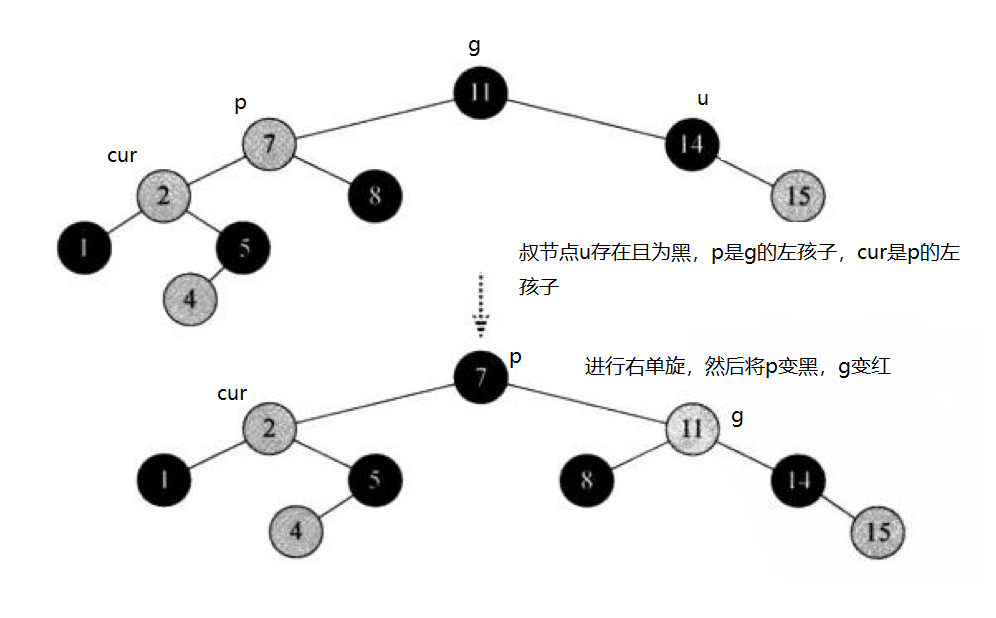
2.2 p和g不同为左孩子或者右孩子

如果p是g的左孩子，而cur是p的右孩子，则需要进行双旋转，先进行左单旋，再进行右单旋。反过来也是一样的。

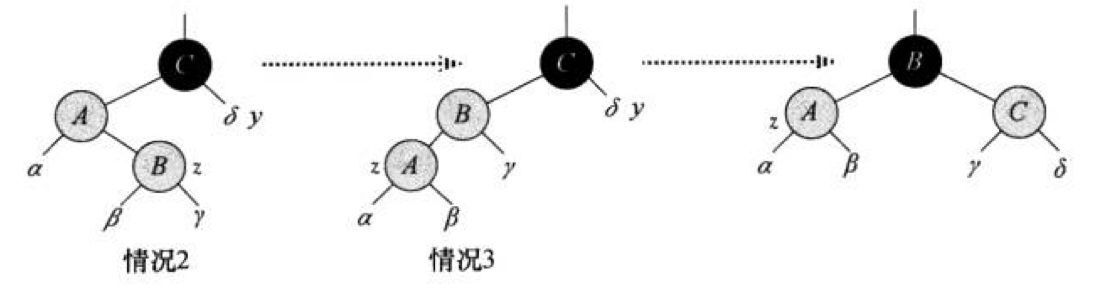
经过一次旋转后也就变成了同为左孩子或者右孩子的情况。

下面给出控制平衡的代码参考：

//控制近似平衡
//如果新增节点的父亲是红色，就需要继续处理
while (parent && parent->_col == Red)
{
    //祖父一定存在且颜色一定为黑
    Node* grandfather = parent->_parent;
    //找到uncle节点
    if (parent == grandfather->_left)
    {
        Node* uncle = grandfather->_right;
        //第一种情况：uncle存在且为红，进行变色处理,并且继续向上处理
        if (uncle && uncle->_col == Red)
        {
            parent->_col = uncle->_col = Black; // 父亲和叔叔变黑
            grandfather->_col = Red; // 祖父变红

            //更新cur
            cur = grandfather;
            parent = cur->_parent;
        }
        //情况二+情况三：uncle不存在，或者存在且为黑，需要旋转+变色处理
        else
        {
            //情况二：右单旋+变色
            if (cur == parent->_left)
            {
                RotateR(grandfather);
                parent->_col = Black;
                grandfather->_col = Red;
            }
            //情况三：双旋+变色
            else
            {
                RotateL(parent);
                RotateR(grandfather);
                cur->_col = Black;
                grandfather->_col = Red;
            }

            break;
        }
    }
    else
    {
        Node* uncle = grandfather->_left;
        //第一种情况：uncle存在且为红，进行变色处理,并且继续向上处理
        if (uncle && uncle->_col == Red)
        {
            parent->_col = uncle->_col = Black; // 父亲和叔叔变黑
            grandfather->_col = Red; // 祖父变红

            //更新cur
            cur = grandfather;
            parent = cur->_parent;
        }
        情况二+情况三：uncle不存在，或者存在且为黑，需要旋转+变色处理
        else
        {
            //情况二：左单旋+变色
            if (cur == parent->_right)
            {
                RotateL(grandfather);
                parent->_col = Black;
                grandfather->_col = Red;
            }
            // 情况三：双旋 + 变色
            else
            {
                RotateR(parent);
                RotateL(grandfather);
                cur->_col = Black;
                grandfather->_col = Red;
            }
            break;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

---

在插入完毕后，一定要记得将根节点强制置为黑。加上这句代码，插入才算完美。

//将根节点强制变黑
_root->_col = Black;
1
2

2.2 删除

对于删除和AVL树一样，不做说明，对于红黑树的学习，主要掌握就是控制平衡的方式。删除也是类似，只不过情况不同。如果想要深入学习，可以看看其他的博客或者《算法导论》这本书。给大家推荐一篇博客，维基百科上的讲解也非常不错。

红黑树插入和删除 - 博客园

红黑树 - 维基百科，自由的百科全书 (wikipedia.org)

2.4 检查红黑树平衡和满足规则

检查平衡

简单走一个中序遍历，看是不是有序的就可以判断平衡

void _InOrder(Node* root)
{
    if (root != nullptr)
    {
        _InOrder(root->_left);
        cout << root->_kv.first << " ";
        _InOrder(root->_right);
    }
}
1
2
3
4
5
6
7
8
9

检查满足规则

红黑树的五条规则：

1. 节点是红色或黑色。
2. 根节点是黑色。
3. 所有叶子都是黑色（叶子是NIL节点）。
4. 每个红色节点必须有两个黑色的子节点。（或者说从每个叶子到根的所有路径上不能有两个连续的红色节点。）（或者说不存在两个相邻的红色节点，相邻指两个节点是父子关系。）（或者说红色节点的父节点和子节点均是黑色的。）
5. 从任一节点到其每个叶子(NIL)的所有简单路径都包含相同数目的黑色节点。

对于上面五条规则。规则四和规则五是维护过程中的主要维护，其他三个都可以满足，所以在检查中，最重要的检查的就是这两条规则。

检查是否出现连续的红色节点

//检查是否存在连续的红节点
bool CheckRED_RED(Node* cur)
{
    if (cur == nullptr)
        return true;

    if (cur->_col == Red && cur->_parent->_col == Red)
    {
        cout << "存在连续的红节点" << endl;
        return false;
    }
    return CheckRED_RED(cur->_left)
        && CheckRED_RED(cur->_right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

检查是否满足每条简单路径上黑色节点的数量相等

//判断每条路径上黑色节点数量是否相等
bool CheckBlackNum(Node* cur, int blacknum, int benchmark) // benchmark为基准数量，在总的检查函数先求出来
{
    if (cur == nullptr)
    {
        if (blacknum != benchmark)
        {
            cout << "黑色节点数量不相等" << endl;
            return false;
        }
        return true;
    }
    if (cur->_col == Black)
        blacknum++;
    return CheckBlackNum(cur->_left, blacknum, benchmark)
        && CheckBlackNum(cur->_right, blacknum, benchmark);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

实现总的检查函数

//判断红黑树是否平衡
bool IsBanlance()
{
    //判断根节点是不是黑色
    if (_root == nullptr)
        return true;
    if (_root->_col == Red)
    {
        cout << "根节点不是黑色" << endl;
        return false;
    }

    // 先算出最左路径的黑色节点的数量作为基准值
    int benchmark = 0;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_col == Black)
        {
            ++benchmark;
        }

        cur = cur->_left;
    }

    int blackNum = 0;
    //对规则四和规则五进行检查
    return CheckRED_RED(_root) && CheckBlackNum(_root, blackNum, benchmark);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

三、总结

3.1 红黑树与AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是$O(lo{g}_{2}N)$，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

红黑树的应用场景：

1. C++ STL库 – map/set、mutil_map/mutil_set
2. Java 库
3. linux内核
4. 其他一些库

---

3.2 红黑树的学习总结

对于红黑树的学习，个人感觉比AVL树简单，情况没有那么复杂，AVL树情况更多，更难理解一点。也有可能我是站在学习完AVL树以后再来学习红黑树的角度来看的，总体上来说，这两种树数据结构都是比较难学的。不过对于今后的学习是很有意义的，可以了解到一些复杂数据结构到底是什么样子的，不能只会用，而不了解具体实现。