-
数据挖掘经典十大算法_NaiveBayes朴素贝叶斯
一、引言
贝叶斯分类是分类算法的总称,该类算法均以贝叶斯定理为基础,因此称为贝叶斯分类。而朴素贝叶斯(Naive Bayes)分类是贝叶斯分类中最简单,最常见的一种分类方法。
朴素贝叶斯算法的核心思想: 通过计算特征概率来预测分类,即对于给出的待分类样本,求解在此样本出现的条件下各个类别出现的概率,哪个最大,就认为此待分类样本属于哪个类别。举个栗子: 有1000个西瓜,生瓜和熟瓜个数差不多,现在要用这些西瓜来训练一个识别生瓜的模型,应该如何做呢?
在日常生活中,我们根据实际经验,挑选西瓜之前会先拍一拍,听声音是清脆还是沉闷。如果我们只通过拍击的声音来辨别是好瓜还是坏瓜,声音清脆说明西瓜还不够熟,声音沉闷说明西瓜成熟。
所以,坏西瓜的敲击声是清脆的概率更大,好西瓜的敲击声是沉闷的概率更大。P(坏瓜声音清脆)—>概率大;P(好瓜声音沉闷)—>概率大
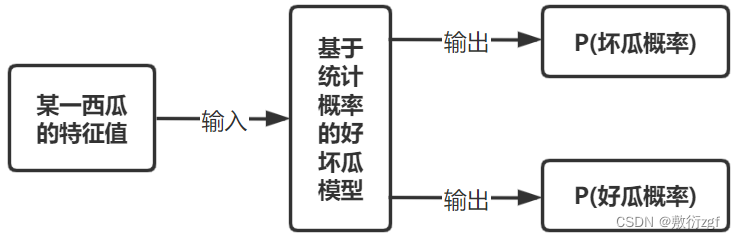
当然这也并不绝对,我们千挑万选地「沉闷」瓜也可能并没熟,这就是噪声了。在实际生活中,除了敲击声,我们还有其他可能特征来辅助判断,例如色泽、根蒂、品类等。朴素贝叶斯把类似拍击声这样的特征概率化,构成一个西瓜的品质向量以及对应的生瓜/熟瓜标签,训练出一个标准的基于统计概率的好坏瓜模型。利用模型,我们在知道某一个西瓜的特征值之后,将其输入到模型中,可以分别输出好坏瓜的概率,根据概率的大小来判别。
二、贝叶斯定理
公式:
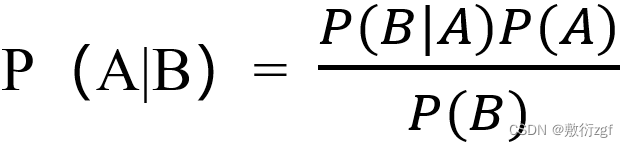
(一)先验概率: 事件发生前的预判概率。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出。一般都是单独事件概率。在公式中P(A)和P(B) 都是先验概率。例如:如果对于某个西瓜的色泽、根蒂和纹理等特征一无所知,按照常理来说,西瓜是好瓜的概率是60%。那么这个概率P(好瓜)就被称为先验概率。
(二)条件概率: 一个事件发生后另一个事件发生的概率,又叫似然概率。在公式中P(B|A) 是条件概率。
(三)后验概率: 事件发生后求的反向条件概率。即基于先验概率求得的反向条件概率。概率形式与条件概率相同。在公式中P(A|B) 是后验概率。例如了解到判断西瓜是否好瓜的一个指标是纹理。一般来说,纹理清晰的西瓜是好瓜的概率大一些,大概是75%。如果把纹理清晰当作一种结果,然后去推测好瓜的概率,那么这个概率P(好瓜|纹理清晰)就被称为后验概率。
三、朴素贝叶斯
重要前提: 每一个事件属性都是相互独立的 ,attributes are conditionally independent
这也是朴素的由来,假设待分类项的各个属性在相互独立的情况下,构造出来的分类算法。朴素贝叶斯模型的基本思想: 对于给定的待分类项X{a1, a2,a3,…,an},求解在此项出现的条件下各个类别yi出现的概率,哪个P(yi|X)最大,就把此待分类项归属于哪个类别。
举个栗子: 有以下一组数据


在朴素贝叶斯算法中,待分类项的各个特征属性条件独立
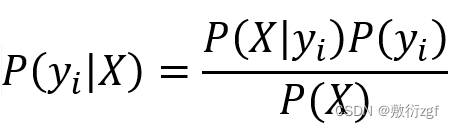
由于公式中分母P(X)表示数据集中每一个特征属性存在的概率,是固定的,因此我们在求解后验概率时一般只考虑分子即可。
又由于每一个特征属性相互独立,
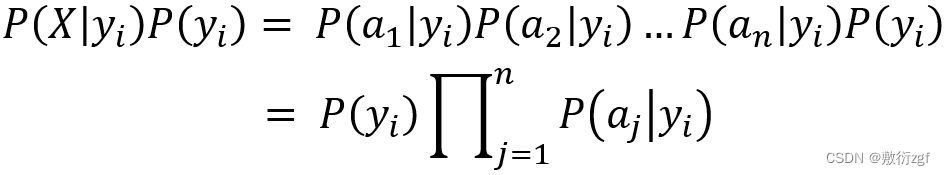
推导出
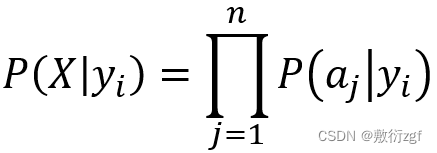
在了解计算公式之后,我们使用公式来解决实际问题吧!四、举个栗子
假设已知一个瓜{‘青绿’,‘稍蜷’,‘沉闷’,‘清晰’,‘稍凹’,‘硬滑’},判断该瓜好不好?
(一)根据贝叶斯公式

(二)转换成分类任务的表达式

(三)开始计算
P(好瓜|青绿 稍蜷 沉闷 清晰 稍凹 硬滑) 和 P(坏瓜|青绿 稍蜷 沉闷 清晰 稍凹 硬滑) 的概率哪个大


分母计算采用全概率公式:

带入数据P(好瓜) = 3/7 P(坏瓜) = 4/7
P(青绿│好瓜)P(稍蜷│好瓜)P(沉闷│好瓜)P(清晰│好瓜)P(稍凹│好瓜)P(硬滑│好瓜)
= (2/3) * (1/3) * (1/3) * (3/3) * (1/3) * (2/3) = 12/729
P(青绿│坏瓜)P(稍蜷│坏瓜)P(沉闷│坏瓜)P(清晰│坏瓜)P(稍凹│坏瓜)P(硬滑│坏瓜)
= (1/4) * (1/4) * (1/4) * (1/4) * (1/4) * (2/4) = 2/4096
P(好瓜) * P(青绿│好瓜)P(稍蜷│好瓜)P(沉闷│好瓜)P(清晰│好瓜)P(稍凹│好瓜)P(硬滑│好瓜)
= 3/7 * 12/729 = 36/5103
P(坏瓜) * P(青绿│坏瓜)P(稍蜷│坏瓜)P(沉闷│坏瓜)P(清晰│坏瓜)P(稍凹│坏瓜)P(硬滑│坏瓜)
= 4/7 * 2/4096 = 8/28672
P(青绿 稍蜷 沉闷 清晰 稍凹 硬滑) = 36/5103 + 8/28672最终:
P(好瓜|青绿 稍蜷 沉闷 清晰 稍凹 硬滑) = (36/5103) / (36/5103 + 8/28672) = 0.9619
P(坏瓜|青绿 稍蜷 沉闷 清晰 稍凹 硬滑) = (8/28672) / (36/5103 + 8/28672) = 0.0380
由于 0.9619 > 0.0380 ,因此 该瓜是好瓜。五、拉普拉斯平滑处理
例如在上述数据集中,好瓜的纹理都为‘清晰’,当假设的数据中出现‘稍糊’和‘模糊’时,此时我们计算出的概率为0,但是在样本数据量足够大的情况下可能性并不为0。
为了解决零概率的问题,法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加法平滑也叫做拉普拉斯平滑。假定数据样本量很大时,每个分量x的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。
六、拉普拉斯平滑处理后的条件概率计算公式
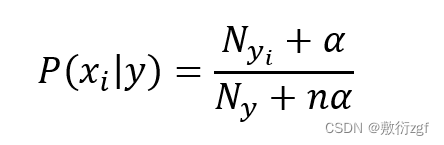
- Nyi表示类别y的所有样本中特征xi的特征值之和;
- Ny表示类别y的所有样本中全部特征的特征值之和;
- n 表示特征总数;
- α 表示表示平滑值(α∈[0,1])主要为了防止训练样本中某个特征没出现而导致Nyi = 0 ,从而导致条件概率P( xi∣ y ) = 0 的情况,如果不加入平滑值,则计算联合概率时由于某一项为0导致后验概率为0的异常情况出现。
-
相关阅读:
浅谈智能安全配电装置应用在银行配电系统中
C++菱形继承
Docker容器数据卷
C语言每日一题(21)删除排序数组中的重复项
std::minus
【MCAL_CANDriver】-2.1-硬件过滤(Hardware Filter)详述及配置
精心整理170道Python面试题,建议收藏!
RabbitMQ 常见面试题
mini_batch学习
实现切换图片透明度轮播效果
- 原文地址:https://blog.csdn.net/qq_45556665/article/details/126324361