Leetcode 216.组合总和III

1.题目描述

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次
  返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例：

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

2.思路分析

相对于77. 组合，无非就是多了一个限制，本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,…,9]。

• k：相当于树的深度
• 9：相当于树的宽度

例如： k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。

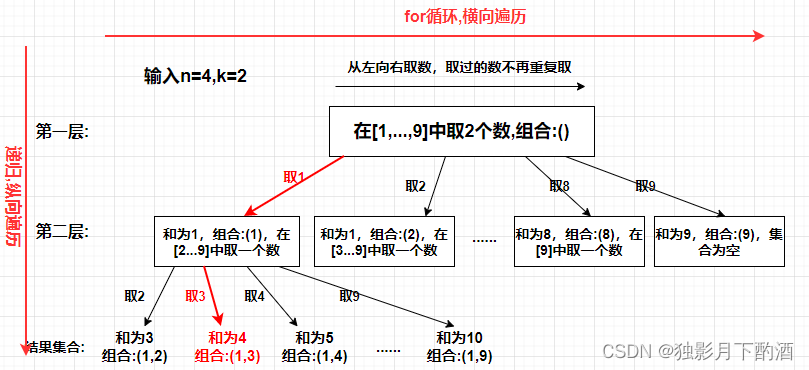
从图中可以看出符合条件的组合为：(1,3)

回溯三部曲：

• 确定回溯函数的参数以及返回值

  # 存放结果集
  result = []
  # 存放符合条件的结果
  path = []
  1
  2
  3
  4

  • targetSum：目标和(对应题目中的n)
  • k：集合元素的个数
  • sum：已收集元素的总和(path中的元素和)
  • startIndex：控制循环的起始位置

  result = []
  path = []
  def backtracking(targetSum:int, k:int, sum:int, startIndex:int)->None:
  1
  2
  3

• 确定终止条件

  path.size == k 就终止了

  如果path中的元素和 == targetSum，result收集结果

   if len(path) == k:  # len(path)==k时不管sum是否等于n都会返回
              if path_sum== n:
                  res.append(path[:])
              return
  1
  2
  3
  4

• 确定单层搜索逻辑

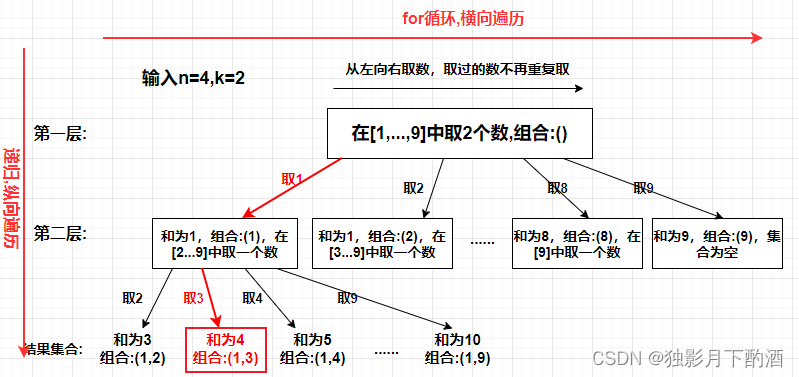
3.剪枝优化

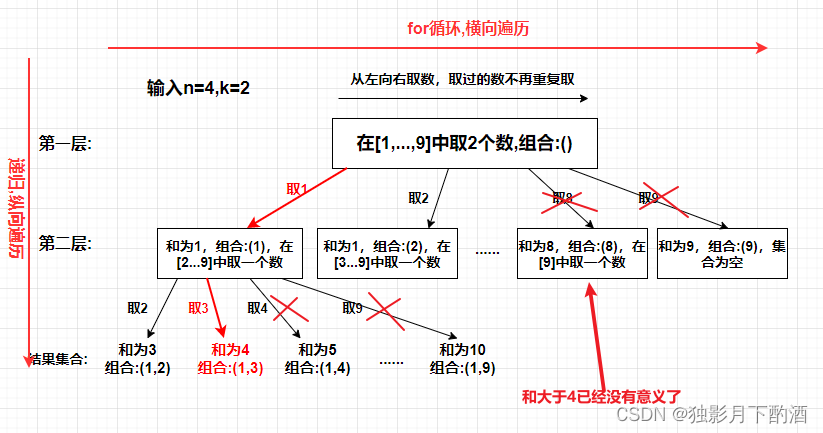
 if path_sum > n:  
            return
1
2

4.代码实现

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        # 定义全局变量
        result, path = [], []

        def backtrack(k: int, targetSum: int, path_sum: int, startIndex: int) -> None:
            # 剪枝操作
            if path_sum > targetSum:
                return 
            # 终止条件
            if len(path) == k:
                if path_sum == targetSum:
                    result.append(path[:])
                return
            # 单层搜索逻辑
            # for i in range(startIndex, 10):[1,...,9]
            # 已选择的元素个数:len(path)
            # 需要的元素个数:k-len(path)
            # 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历
            for i in range(startIndex, 10 - (k - len(path)) + 1):
                # 处理节点
                path.append(i)
                path_sum += i
                # 递归
                backtrack(k, targetSum, path_sum, i + 1)
                # 回溯
                path.pop()
                path_sum -= i

        backtrack(k, n, 0, 1)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

注:

result.append(path)产生错误的结果，而result.append(path[:])会产生正确的结果

区别:

result.append(path) : 将path这个列表地址添加到result中，因此当后面path改变时，result中的path会不断发生改变，并不会保存当时想要得到的结果

result.append(path[:])是将path列表中存储的值复制到一个新的地址中去，result是添加新的地址的值，因此后面无论path的值如何改变，都不会影响这个添加进去的值，因此在通常保存列表结果时，应该使用path[:]