-
堆排序(思路分析) [数据结构][Java]
堆排序(思路分析)
堆是一种特殊的数据结构: 堆是使用数组实现的二叉树
堆排序的基本介绍:
①堆排序是利用堆这种数据结构而设计的一种对数组元素的排序算法, 堆排序是一种选择排序, 它的最好, 最坏, 平均时间复杂度都是O(nlogn)
- 注意: 堆排序是一种不稳定的排序算法
②堆是具有以下性质的完全二叉树
- 每个结点的值都大于或者是等于其右子节点和左子节点的值, 我们称之为大顶堆, 如果每个结点的值都小于或者是等于当前结点的左右子节点的值, 我们就称之为小顶堆
- 我们并没有要去当前节点的左右子节点的大小关系, 也就是只要是每个结点的值都大于等于或者小于等于当前节点的左右子节点的值, 我们就将这个数组称之为堆结构
大顶堆举例说明: (图解)
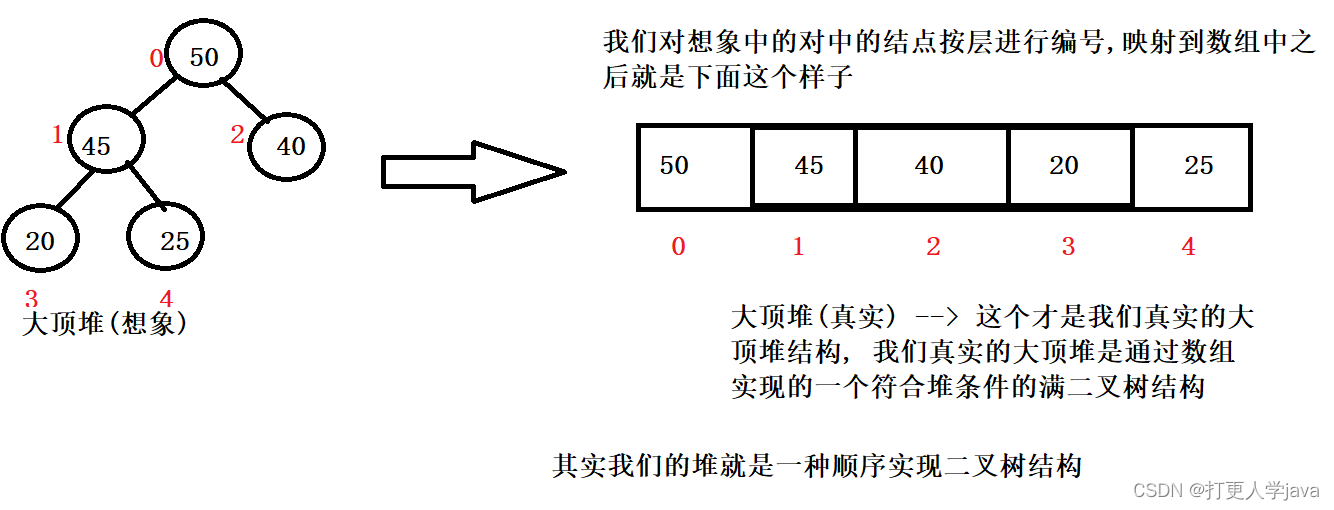
我们前面在学习顺序存储二叉树的时候学习过: 对于顺序存储二叉树中2 * i + 1的位置是顺序存储二叉树中i位置的左子节点, 2 * i + 2的位置是顺序存储二叉树中的i位置的右子节点位置
- 所以有以下结论:
- 对于大顶堆: arr[i] >= arr[2 * i + 1] && arr[i] >= arr[2 * i + 2]
- 对于小顶堆: arr[i] <= arr[2 * i + 1] && arr[i] <= arr[2 * i + 2]
我们一般升序中都是采用大顶堆, 降序测试采用小顶堆
那么为什么是这样?
这里我们以升序为例进行讲解, 我们在堆排序中最终每次排好序之后, 也就是将所有的结点转换为一个堆结构之后, 这个时候我们每次都要将我们的堆顶元素和我们的堆中最后一个元素(也就是实现堆结构的底层数组中的最后一个元素) 进行一个值交换, 那么如果我们是一个大顶堆, 这时候每一次其实都是将我们的堆中最大的值放到了数组中的最后一个位置, 然后第二次的时候就是将我们的数组中的第二大值(其实也就是堆中的第二大值)放到了数组中倒数第二个元素的位置上, 然后最终就会变成一个有序的升序序列
- 所以我们一般升序都是采用的大顶堆进行排序, 如果我们是要降序还采用大顶堆, 这个时候我们最终得到的结果还要进行一个逆序的操作
堆排序的核心思想:
- 将待排序序列构建成一个大顶堆
- 此时, 整个序列中的最大值就是堆顶的根节点了
- 将堆顶的根节点和数组中的末尾元素进行一个交换, 此时数组末尾就是堆中(其实也就是数组中)的最大值
- 然后将剩余的n - 1个元素重新构建成一个大顶堆结构, 这样我们就会得到n个元素中的次小值, 如此反复执行, 最终就能得到一个有序序列了
- 在这个重复的过程中, 要构建成为大顶堆的元素逐渐减少, 最终当只剩下堆顶元素一个元素的时候, 这个时候我们就是得到了一个有序序列了
堆排序的思路分析:(这里我们以升序为例, 那么就是采用大顶堆)
我们先编写一个方法, 用于将我们的指定的结点作为根节点的子树转换为一个大顶堆结构, 因为我们开始的时候肯定是拿到了一个无序的原始数组, 然后我们要将这个数组转换为一个大顶堆, 转换为大顶堆之后将堆顶元素和数组中的最后一个位置的元素进行一个值交换, 那么数组中最后的一个元素此时就是堆中的最大值了, 然后我们继续将剩下的元素转换为堆:
-
我们首先要解决的问题就是我们如何将这个数组转化为一个大顶堆, 那么我们要如何转化?
-
我们要确保我们的每个结点的值都要大于当前节点的左右子节点的值, 所以我们要从堆的最下面开始向上进行遍历转化, 每次先将我们的开始的时候不满足要求的满二叉树结构的最下面的非叶子结点转换为一个局部大顶堆, 然后一点一点的前遍历, 等到最终遍历到根节点的时候我们的整个数组就是满足大顶推结构的要求了
-
这里我们注意: 这里我们一定要是从最后一个非叶子结点开始遍历, 首先是为了让堆中的子树满足大顶堆的要求, 那么我们肯定是要从非叶子结点开始, 因为叶子结点其实就不是一个子树, 叶子结点没有左右子节点, 所以我们对于叶子结点其实就是不用调用转换为堆的方法的, 我们的叶子结点下面是没有子节点的, 所以我们肯定是将非叶子结点转化为堆结构才是有意义的, 并且我们最终要让整个数组都满足大顶堆的条件, 这个时候我们一定是从最后一个非叶子结点开始的, 然后我们将最后一个非叶子结点所在的子树调整为满足大顶堆的要求之后, 我们就开始操作倒数第二个非叶子结点即可, 然后我们要让倒数第二个非叶子结点也满足我们的大顶堆的要求, 然后一直向前遍历, 直到遍历到堆顶元素为止 , 那么等处理完堆顶元素之后这个数组就是完全满足大顶堆的要求了
- 然后我们将堆顶元素和堆中的最后一个元素进行一个值交换, 然后我们的数组中最后一个位置的值就是我们的数组中的最大值了(也就是堆中的最大值), 然后我们对堆中除了最后一个元素之外的元素再转换为一个大顶堆
- 注意: 当我们将堆顶元素和最后一个元素交换了位置之后我们下一次就不需要重新从最后一个非叶子结点位置开始遍历转换了,我们只需要从堆顶元素开始遍历就可以了, 因为我们只是交换了堆顶元素和数组中末尾的元素, 这个时候我们的数组中除了堆顶元素和最后一个元素之外的其余位置的元素其实都是符合大顶堆的要求的, 而我们的数组末尾的元素我们不用去管, 那么也就是我们此时只是堆顶元素是不符合我们的要求的 — > 所以我们直接从堆顶元素开始处理一次即可, 处理好之后我们继续重复交换, 然后继续处理堆顶元素
- 直到最终我们的待处理堆中没有非叶子结点为止, 也就是知道我们待处理堆中只有一个堆顶元素为止, 那么此时我们的数组中的元素就会是升序排序的
- 注意: 当我们将堆顶元素和最后一个元素交换了位置之后我们下一次就不需要重新从最后一个非叶子结点位置开始遍历转换了,我们只需要从堆顶元素开始遍历就可以了, 因为我们只是交换了堆顶元素和数组中末尾的元素, 这个时候我们的数组中除了堆顶元素和最后一个元素之外的其余位置的元素其实都是符合大顶堆的要求的, 而我们的数组末尾的元素我们不用去管, 那么也就是我们此时只是堆顶元素是不符合我们的要求的 — > 所以我们直接从堆顶元素开始处理一次即可, 处理好之后我们继续重复交换, 然后继续处理堆顶元素
- 然后我们将堆顶元素和堆中的最后一个元素进行一个值交换, 然后我们的数组中最后一个位置的值就是我们的数组中的最大值了(也就是堆中的最大值), 然后我们对堆中除了最后一个元素之外的元素再转换为一个大顶堆
-
那么我们如何定位到堆中的最后一个叶子结点?
-
我们直接通过 : 堆中元素个数 / 2 - 1 公式就可以定位到堆中最后一个非叶子结点的位置了
-
那么这个公式又是如何推导而来的?(推导思路如下:)
-
我们知道堆是一个完全二叉树结构, 所以最后一个非叶子结点肯定满足如下的条件(最后一个非叶子结点在堆中的位置为x)
-
(arr.length - 1) = 2x + 1 或者是 (arr.length - 1) = 2x + 2
- 上面的arr.length就是堆结构底层数组的长度, 那么arr.length - 1就是表示堆中最后一个叶子结点的索引位置
- 上面的x是我们的最后一个非叶子结点在数组中的索引位置
- 其实这个公式就是因为我们的arr.length - 1可能是最后一个非叶子结点的左子节点, 也可能是最后一个非叶子结点的右子节点, 所以上面才有一个或者关系
-
那么满足了上面的条件之后我们就来进行一个推导:
①arr.length - 1 = 2x + 1 或者 arr.length - 1 = 2x + 2②那么x = (arr.length - 2)/2 或者 x = (arr.length - 3)/2
③那么x = arr.length/2 - 1 或者 x = arr.length/2 - 3/2
④那么由于整数运算中3 /2的结果也是1, 所以有 x = arr.length / 2 - 1, 所以我们就得到了最终的结果
-
-
-
-
-
那么具体的我们如何将对应非叶子结点所引导的子树成为一个大顶堆?
-
我们让当前非叶子结点的左子节点和右子节点进行一个比较, 如果右边的值大, 这个时候我们就用这个当前的非叶子结点和右子节点进行比较, 如果这个右子节点的值大于当前的非叶子结点的值, 那么我们就交换这两个值, 那么我们继续去判断当前右子节点所引导的右子树上判断有没有比自己的值更大的, 如果有,那么就继续交换
-
但是由于我们这里是从下到上递归的, 所以我们很多人认为其实不用去右子树上判断后面的位置的元素,那么这个时候到底要不要循环遍历到右子树上去判断?
-
这个时候是需要的, 我们想一下, 如果我们从最后一个非叶子结点开始向前遍历的时候其余部分都是符合我们的大顶堆的要求的, 然而我们的堆顶元素的值非常的小, 有多小? --> 我们假如这个时候堆顶元素的值要比我们的堆中最后一个位置的值还要小, 那么此时如果我们只是遍历一次, 这个时候会发生什么样的问题? --> 这个时候我们就会只是将我们的堆顶元素和我们的堆顶元素的左右子节点进行了一个值的判断, 也就是我们是先进行判断堆顶元素的左右子节点的值的大小, 假如这个时候我们的右子节点的值更加的大, 此时我们就会是使用这个堆顶元素和我们的右子节点值进行一个交换的操作, 但是这个时候交换了之后问题也就出现了 —> 我们是要变成一个大顶堆, 这个时候要求判断之后的结点的子节点位置的值都要比当前结点的值小, 所以我们一定是要使用当前节点和所有子节点, 孙结点进行判断,保证成为一个大顶堆
- 所以我么就是要循环遍历到右子树中去, 也就是这个时候堆顶结点的右子节点的值如果是比我们的堆顶元素的值大的时候我们先不直接进行元素值的交换,而是先将我们的较大的值赋给我们的堆顶元素的位置, 然后继续使用堆顶元素的右子节点作为子堆的堆顶结点继续进行一个判断, 如果这个时候子堆堆顶元素的值还是要比子堆堆顶元素的右子节点的值小, 那么此时就将我们的子堆对顶元素的值赋给我们的子堆的堆顶元素位置, 然后一直向下继续遍历, 直到遍历到将右子树比那里完为止, 那么这样我们就将这个比较小的值放到了自己应该存在的位置
-
-
-
补充:
此时我们向左子树遍历之后不是一直判断左子节点的值和当前更新后的非叶子结点的值的大小,而是会判断当前更新后结点的左右子节点中的值大的结点来和我们的当前更新后的非叶子结点的值进行一个比较,我们每当判断出有一个子节点(左子节点或者是右子节点)的值比我们的当前非叶子结点的值要大, 那么这个时候我们就要判断对应的值比我们的当前非叶子节点值大的结点所在的子树,判断是否还有比我们的这个结点值更加大的结点值,如果有的话继续循环,直到将这个值放到对应的应该存在的位置为止\
算法核心:
其实堆排序就是合理使用了堆这个数据结构, 通过每次将我们的待排序序列转换为一个大顶堆然后每次得到的堆顶元素就是最大元素, 然后将这个最大元素放到数组中的末尾, 然后对除了这个末尾元素的娶她元素继续开始重新转换为一个大顶堆, 然后继续筛选出当前最大值元素, 然后一直重复, 最开始的时候我们肯定是要将最大值放到最末尾, 然后是倒数第二个位置, 当最后一次的时候就是放到第二个位置, 因为最终最后一个的位置肯定是合理的
算法难点:
要注意: 最开始的时候我们是从堆的底部最后一个非叶子结点开始逐渐向上, 对每个非叶子结点都要转换为大顶堆, 然后最终到了根节点之后才能保证是一个真正的大顶堆, 但是在第一次大顶堆转换完成之后, 其余的时候我们就只用对根节点进行一次转换即可, 因为其他位置肯定是满足大顶堆的要求的, 因为其他位置的元素都没有变, 而其他位置我们第一次的时候都是转换过了
-
相关阅读:
day01-3-界面显示&用户登录&餐桌状态显示
森林防火综合解决方案
用了那么久的Lombok,你知道它的原理么?
【历史上的今天】7 月 21 日:施乐退出计算机市场;《世界版权公约》制定;苹果推出 Apple Airport
【LeetCode75】第七十二题 无重叠区间
【MicroPython】RP2040 MicroPython固件烧录以及Thonny 开发初探
软件供应链攻击的新形式
java.lang.Enum类下equals(Object other)方法起什么作用呢?
利用Bootstrap的分页组件实现分页效果
尺取法总结
- 原文地址:https://blog.csdn.net/m0_57001006/article/details/126457094