-
Unity --- 向量
1.向量是有方向的标量,标量只有值(大小)而没有方向的量
2.向量的模就是向量的大小 : 求模长的公式:头减尾的平方和取根号后的值
3.单位向量 : 大小为1的向量 -- 方向不定
4.向量单位化,归一化 : 将当前向量转为其方向上的单位向量
向量的运算
1.向量的加法运算:
设向量a (x1,y1) , 向量b(x2 , y2)
a+ b = 向量c --- > 向量c(x1 + x2 , y1+y2)
2.向量减法
a -b = 向量c ---> 向量c (x1 - x2 , y1 - y2)
3.向量乘法 ---> 向量只能够和标量相乘,设标量d
a * d = 向量c ---> 向量c (d * x1 , d * y1)
4.向量点乘 ---> 两个向量之间进行点乘得到的是一个标量 --- 快速求两个向量之间的夹角

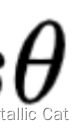
上面这个sitar是两个向量之间的夹角 --- 向量夹角如何求得? --- 将两个向量的起始点平移到同一个起点(一般是原点),此时两个向量之间的夹角就是向量角
5.向量叉乘 --- 用来快速求得某一个面的法向量

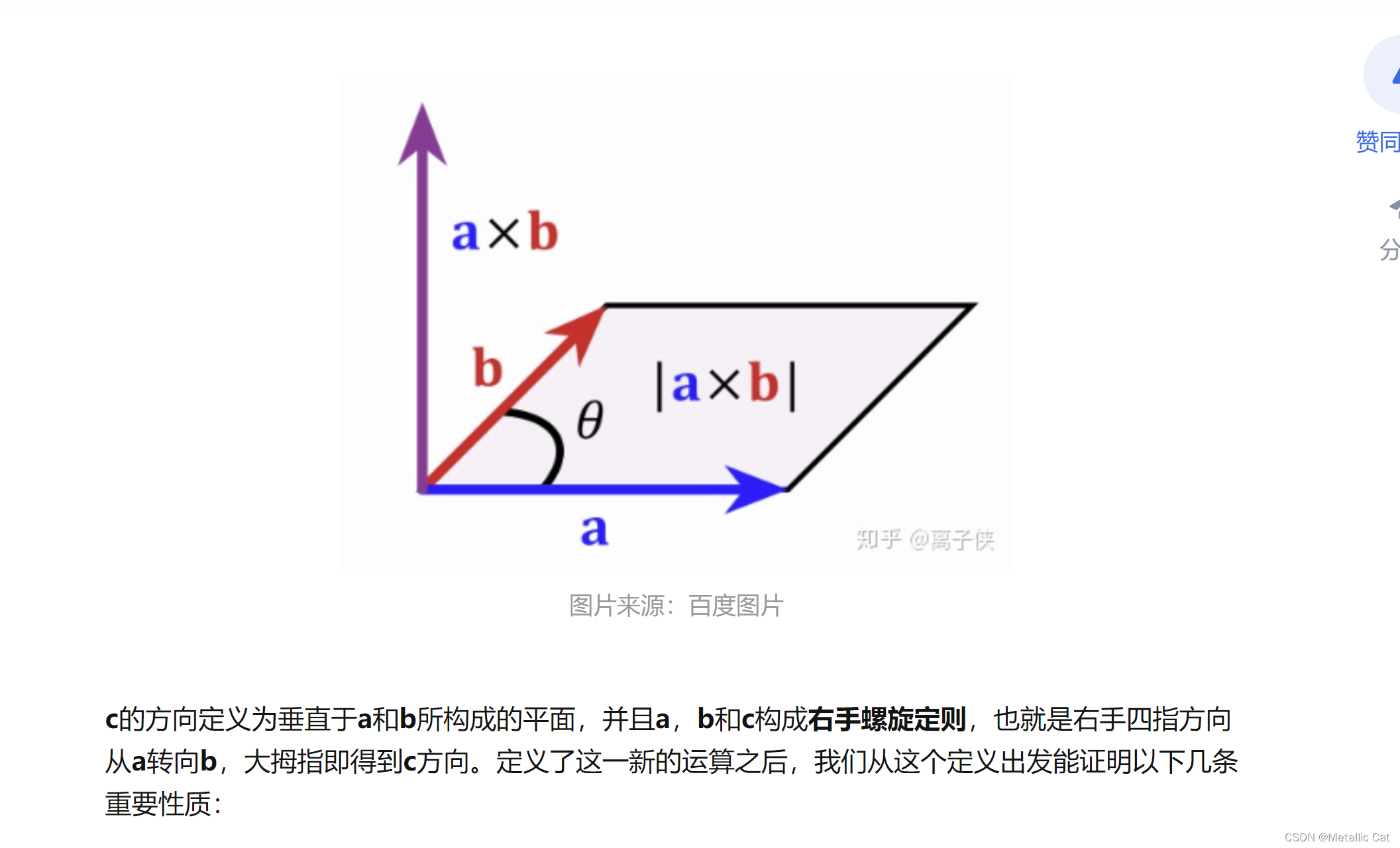
下面这个是向量叉乘的三条性质
ps:a叉乘b,则右手法则从a转向b,得向量c的方向
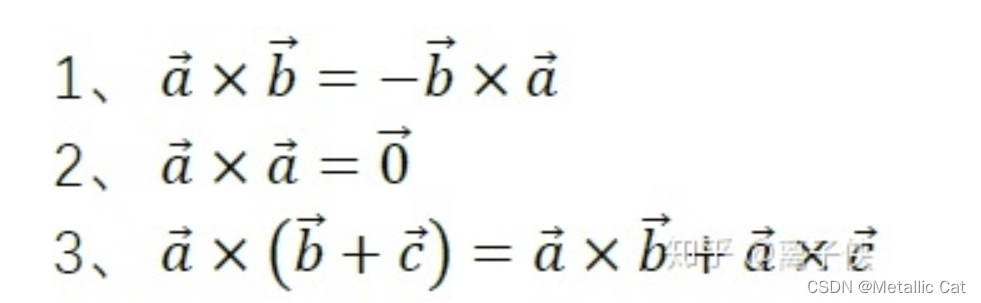
-
相关阅读:
PBR系列-物理材质(上)
xen-trap
leetcode经典题库(简单)
I/O多路复用【Linux/网络】(C++实现select、poll和epoll服务器)
8月19日PMP成绩,预计10月16日公布!附查询入口、流程
c++日期类的实现
AIoT通用组件服务攻略之快速定位http数据推送失败
纯前端js中使用sheetjs导出excel,并且合并标题
哪个才是最适合你的 Web UI 自动化测试框架
C++:mutable 关键字
- 原文地址:https://blog.csdn.net/qq_51947882/article/details/126453062