2022 深度学习 & 计算机视觉 & 感知算法 面经整理 二十五（241 242 243 244 245 246 247 248 249 250）

241 为什么要用MLP，多层全连接网络

MLP：拟合非线性。这个观点的错的！！！！
MLP如果不加激活函数，永远都是线性的。









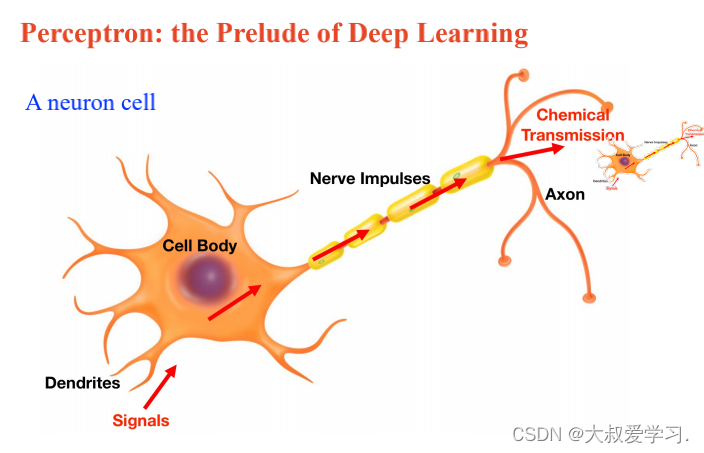
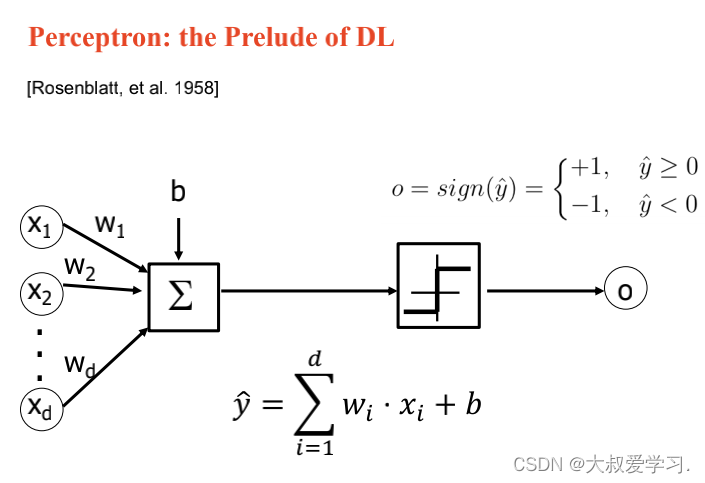
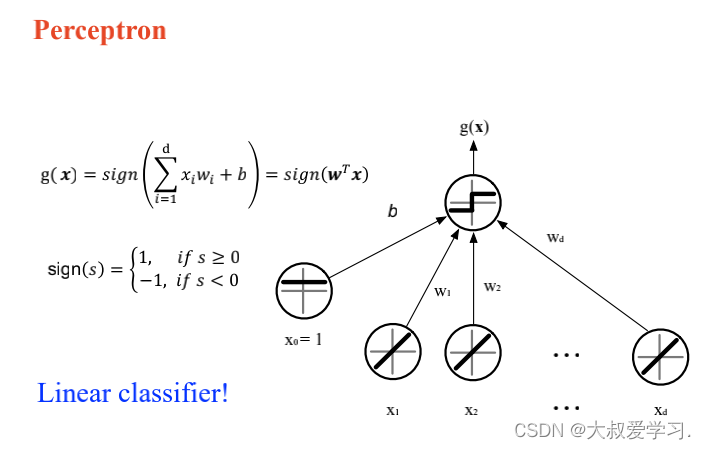
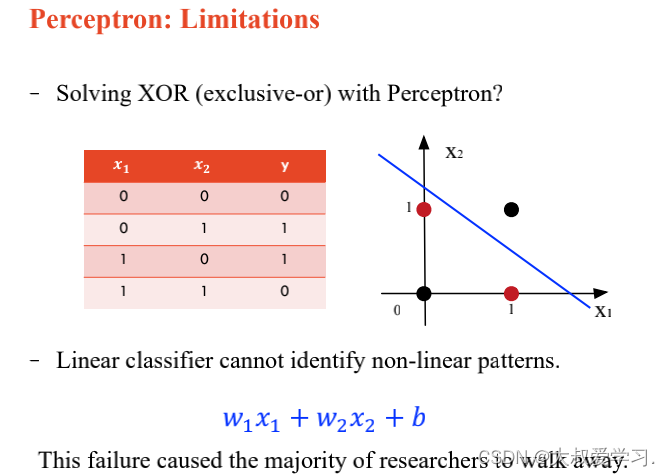
上面说了解决不了XOR的问题，所以用MLP。MLP可以拟合任意连续函数。






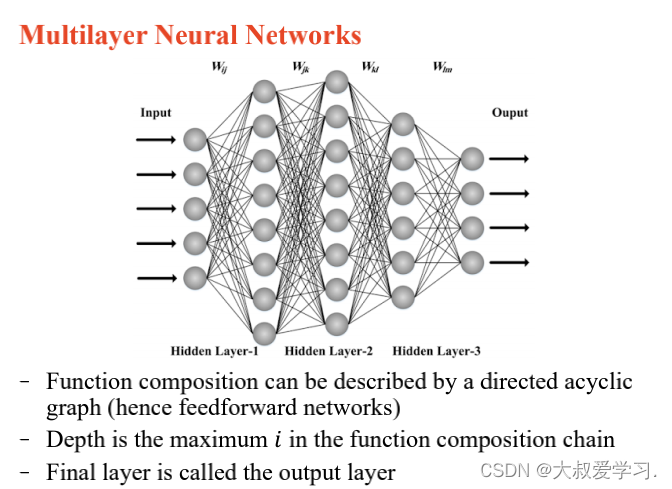
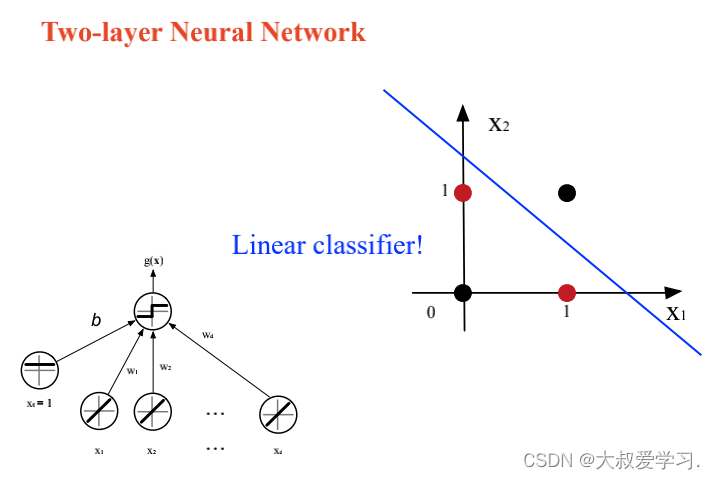
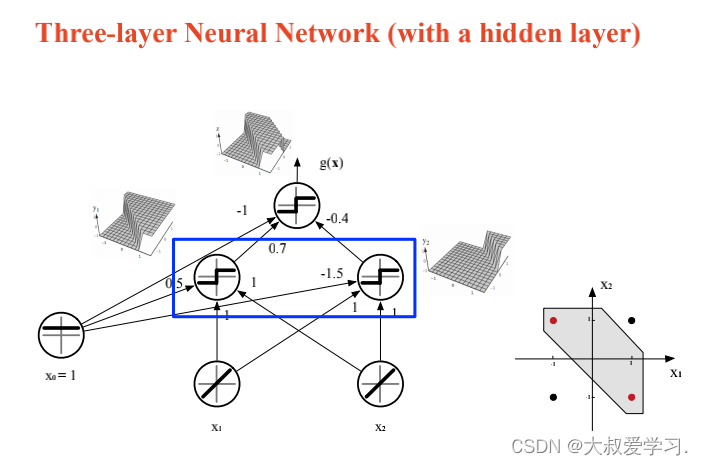
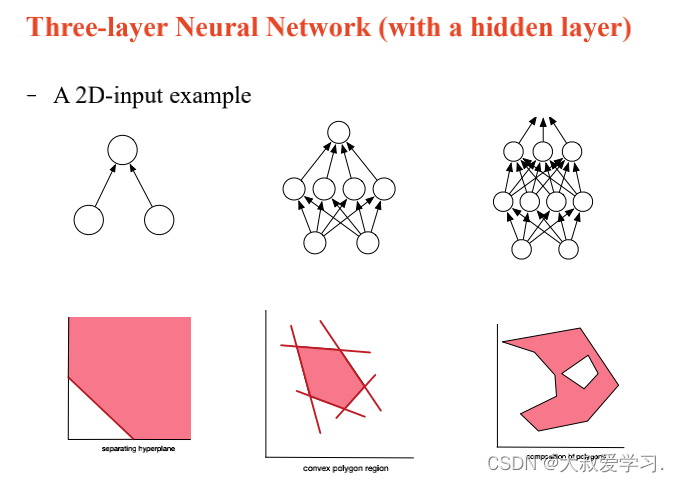
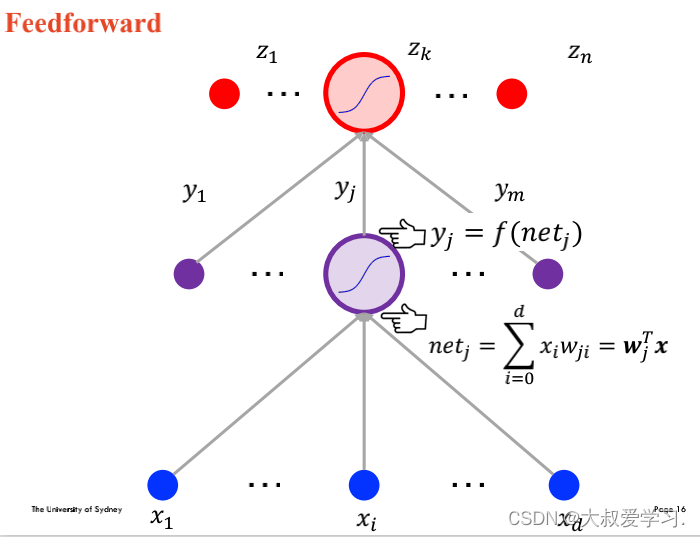
万能逼近定理 Universal Approximation Theorem

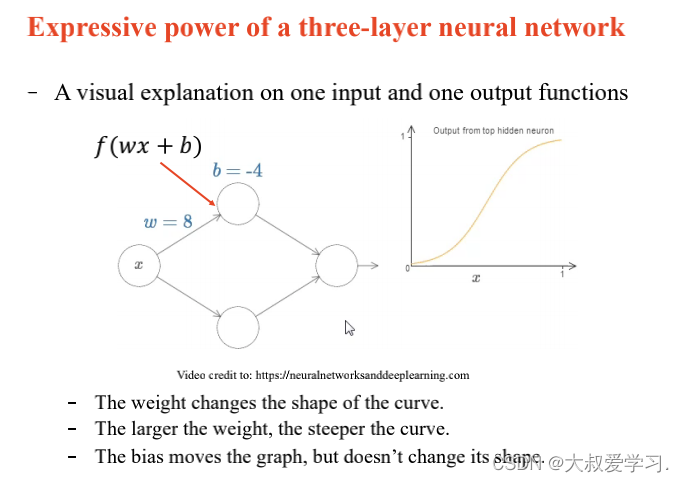
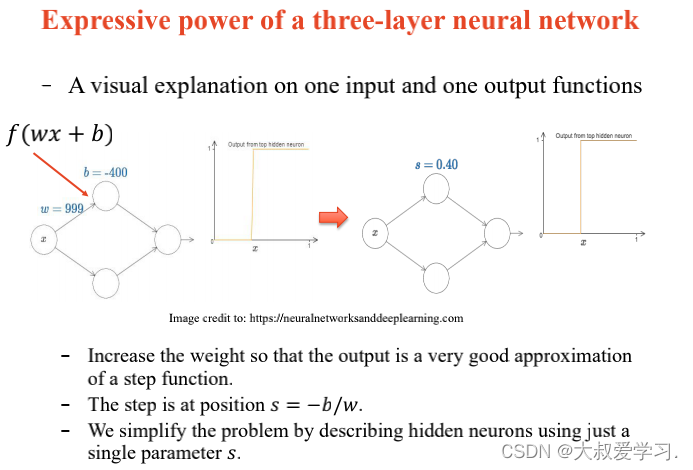
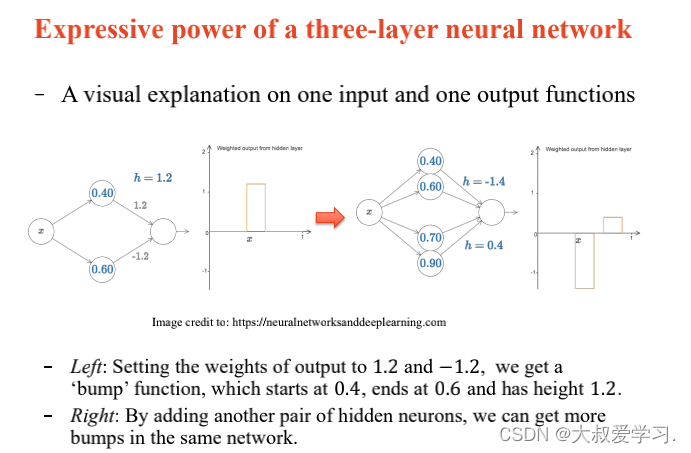
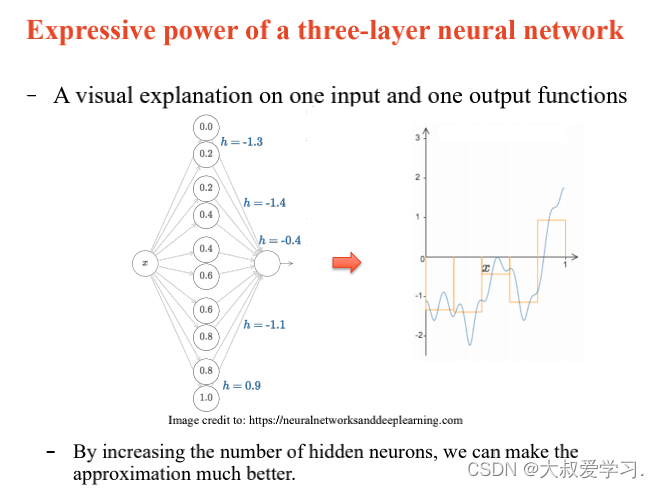
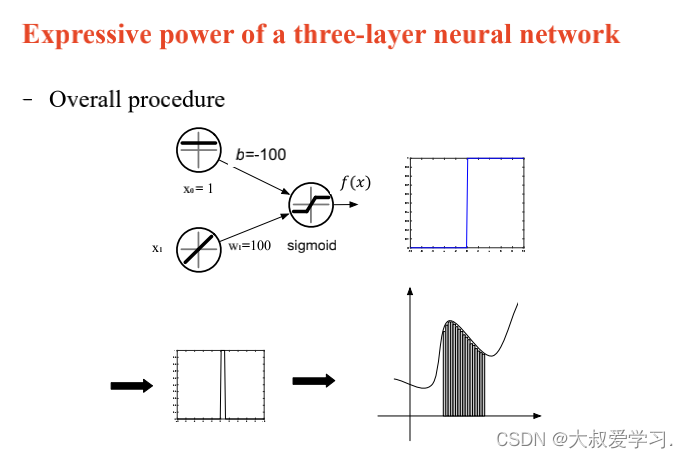
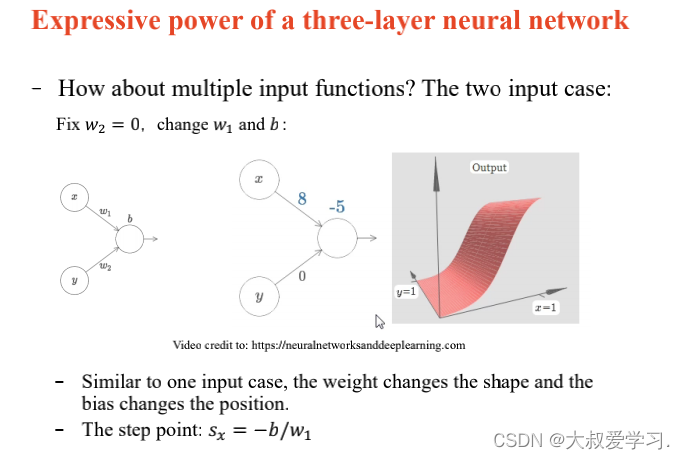
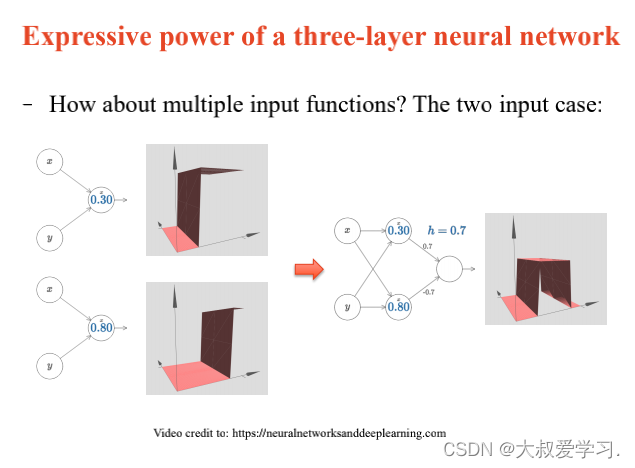
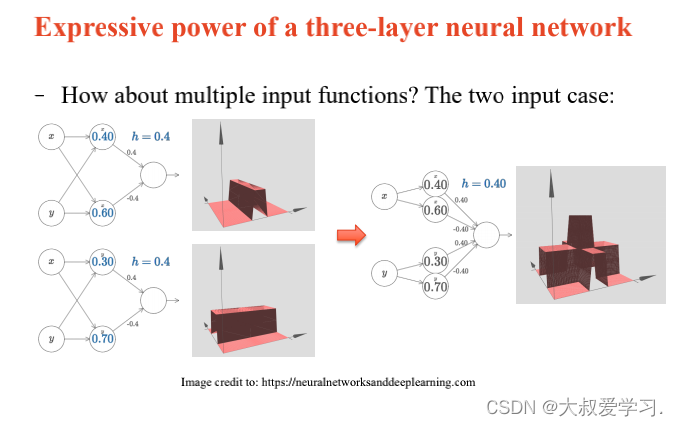
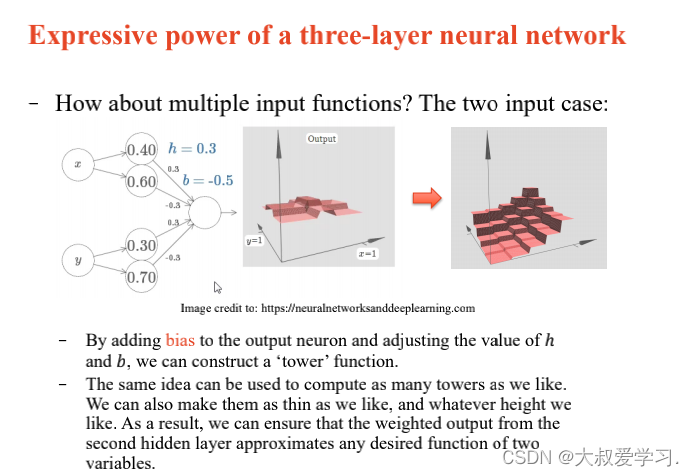
242 backpropogation过程

Backpropogation是修改kernal的weight参数，修改每一个全连接神经元的权重w和b。这些参数都是有初始化的，然后通过训练，计算损失函数，对每一个weight求偏导数，反向传播，更新每一个weight。







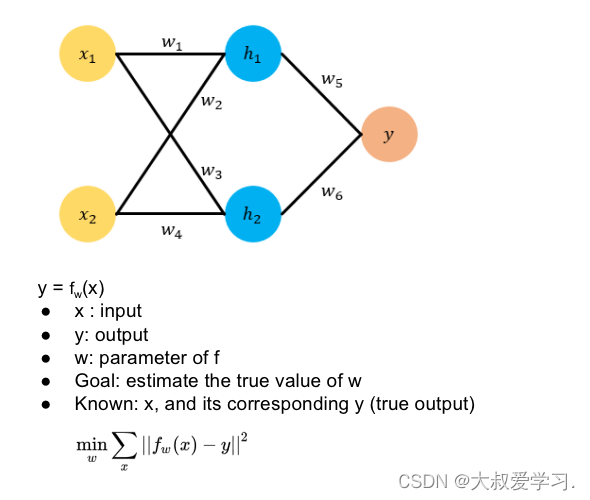
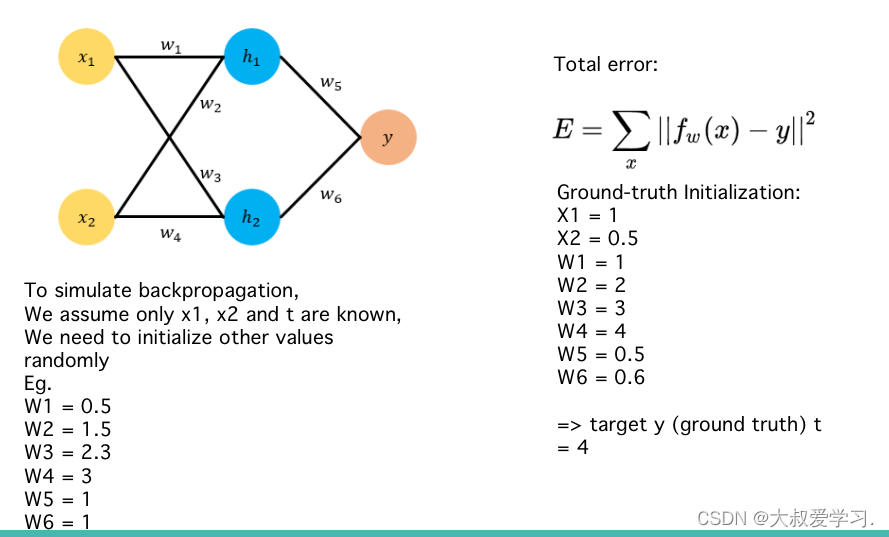
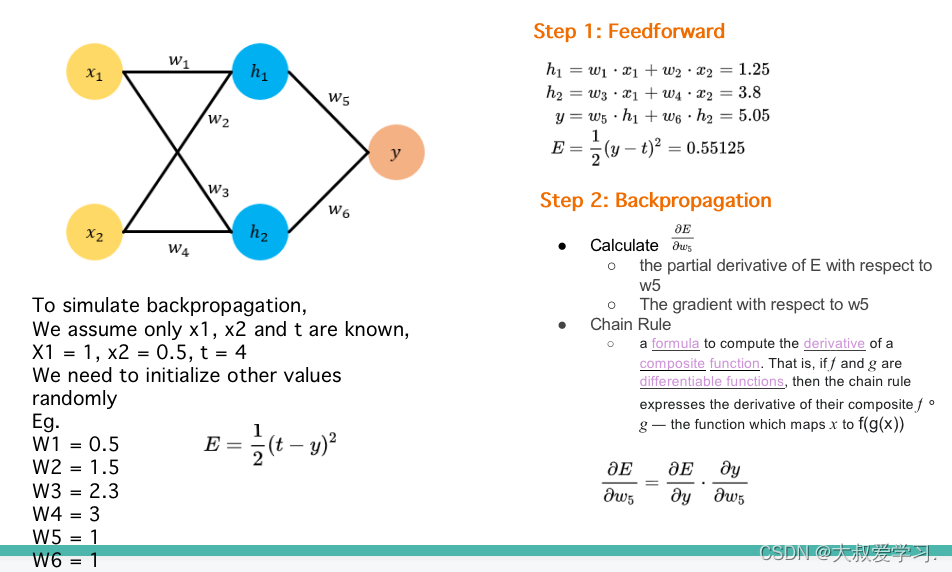
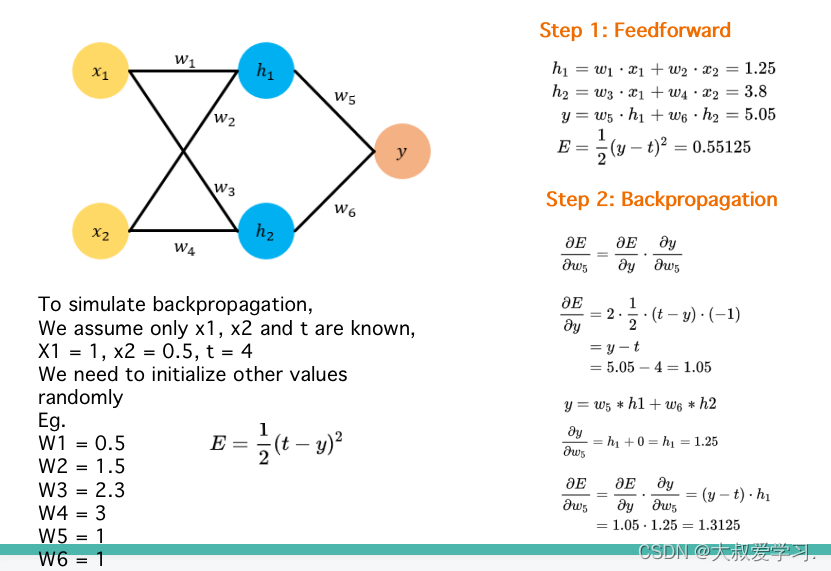
手动实现，还是要用pytorch的矩阵更新方式。

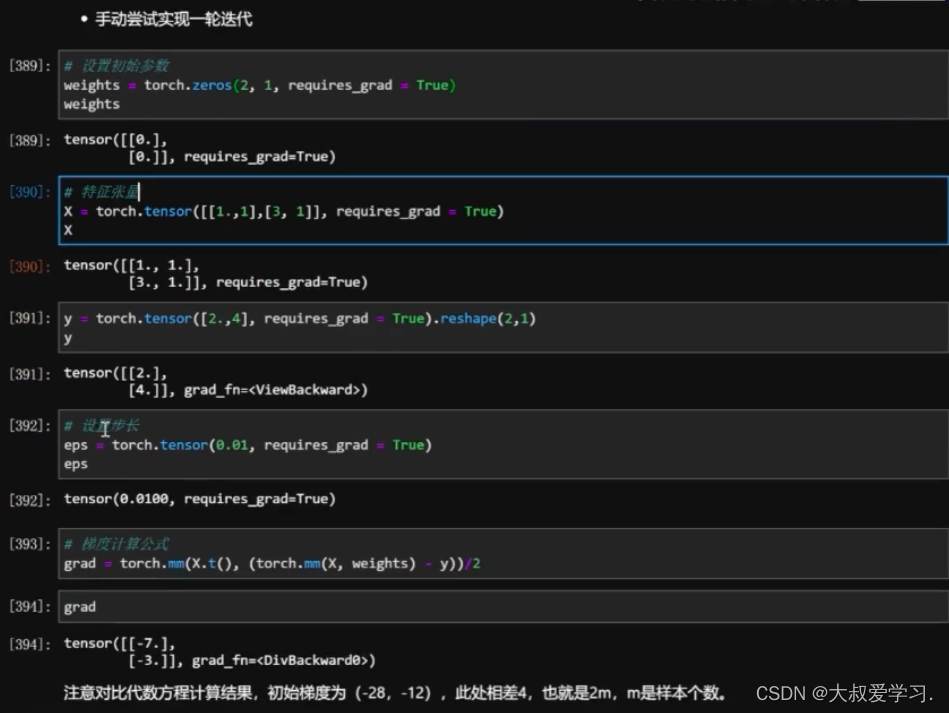
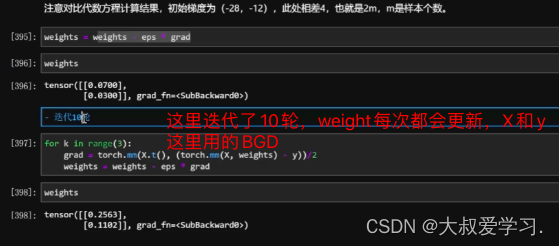
最后返回一个SSE的值。趋近于0.

243 带激活函数的反向传播，如何计算

244 网络 如何识别细颗粒度特征

基于全卷积注意力网络的细粒度识别方法在计算和准确度上都有非常强大的优势。本文首先将介绍什么是细粒度识别，以及一般的细粒度识别方法，然后重点解析百度基于强化学习和全卷积注意力网络的细粒度识别模型。

具体模型相关，参见：https://blog.csdn.net/qq_25439417/article/details/82764183

245 faster RCNN系列 RPN网络解释清楚， Loss公式是什么，ROI Pooling怎么做的

关于faster RCNN 的一切，看着两个。
解读：https://zhuanlan.zhihu.com/p/31426458
代码：https://zhuanlan.zhihu.com/p/145842317

246 如何解决数据长尾（不平衡）问题？

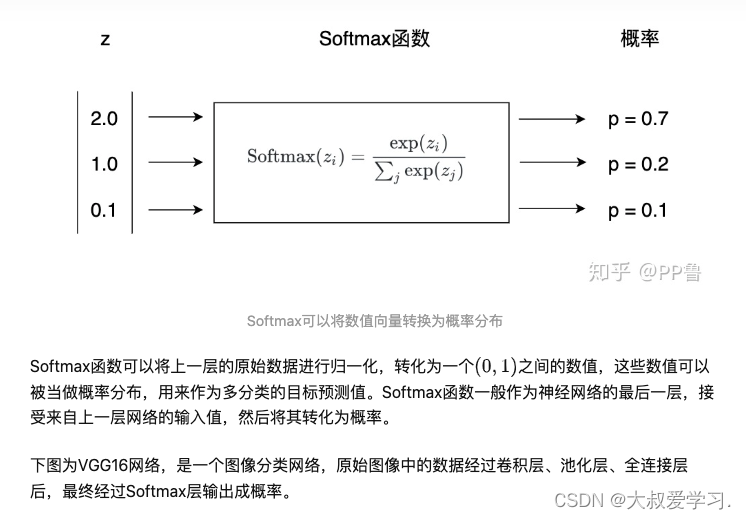
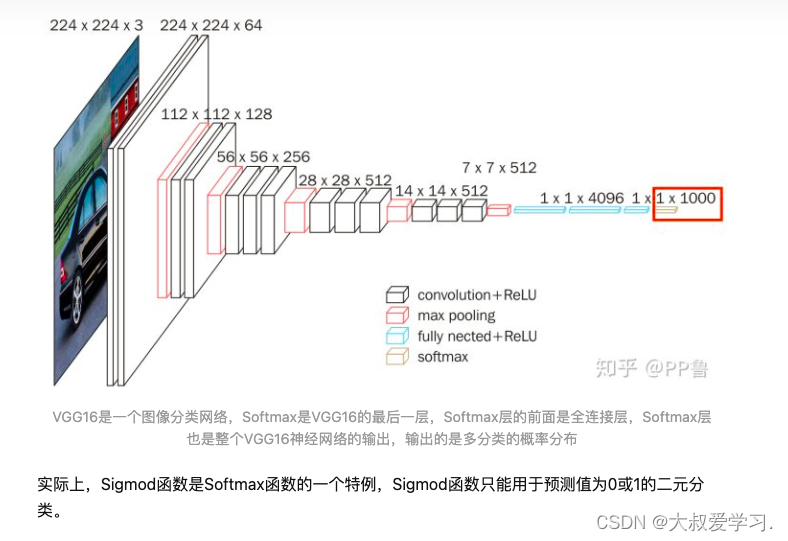
247 softmax公式

Softmax是一种激活函数，它可以将一个数值向量归一化为一个概率分布向量，且各个概率之和为1。Softmax可以用来作为神经网络的最后一层，用于多分类问题的输出。Softmax层常常和交叉熵损失函数一起结合使用。

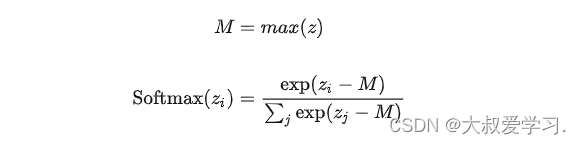
248 CNN权重共享问题？

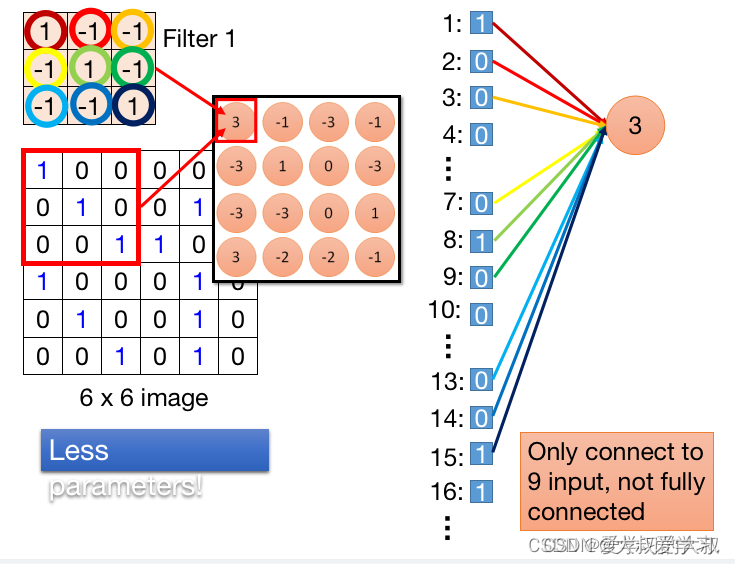
可以看到，CNN神经元链接下一层时，不是全连接的，由上图可以看出，Filter1 对于图片的左上角来说，它只作用于pixel=1，2，3，7，8，9，13，14，15。Filter里面对应的值，可以看到就是DNN的input与神经元3的连线。不同的位置对应不同的颜色。如果是fully conected，一个neuron应该连接36个input（全部的pixel）。但是如果用了Convolution，就只需要连接Filter的大小个。所以我们就用了比较少的参数来完成这个事情。卷积核的参数，就是weight，这点一定要特别注意。

从上图可以看出，-1的neuron分享的input是2，3，4，8，9，10，14，15，16.这里特别注意，neuron 3和neuron -1，其实有一些weight是share的。比如neuron 3 的input 2 和neuron -1 的input 2是共享的。这就意味着卷机操作，使用了更少的参数，因为它们之间的weight是相互share的。在反向传播的过程中，neuron 3 反传input 2 会更新2->3的weight，，neuron -1 反传 input 2 会更新-1->2的weight。这里weight怎么是共享的呢？

249 极大似然解释下

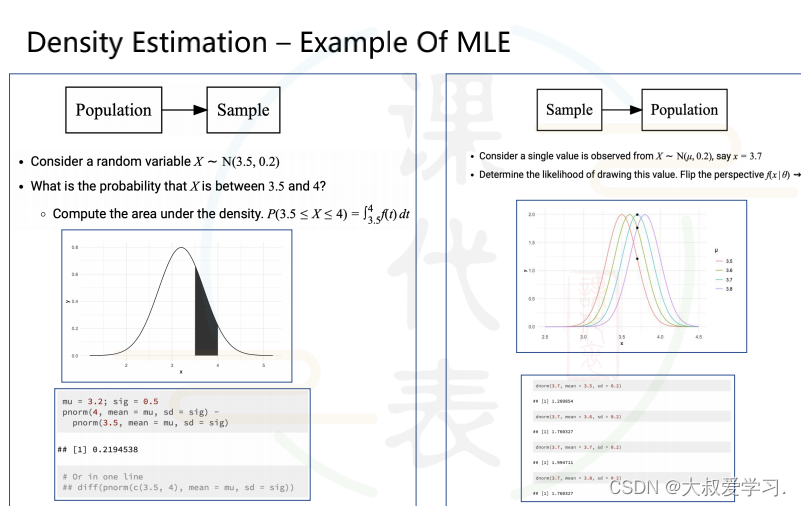
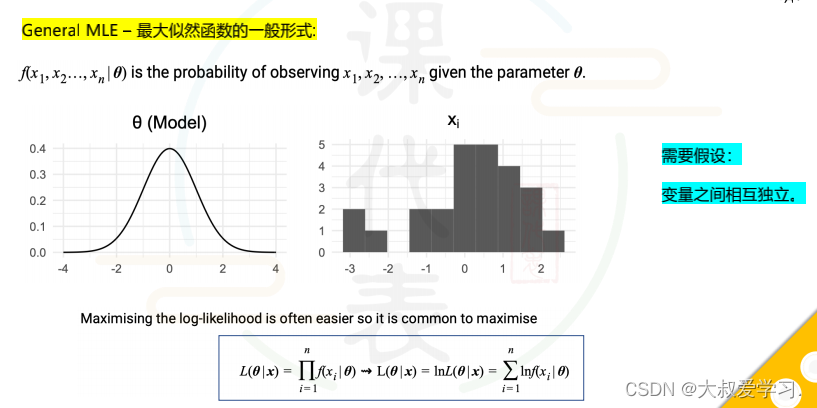
为什么用损失函数而不用准确率作为模型训练目标，因为准确率是不可以求导的，损失函数一般是凸函数，可以用优化方法（梯度下降）来求导。但是由于我们做分类时，一般用的sigmoid或者tanh，输出的都是概率，那么我们就用交叉熵损失来定义分类函数的损失。

250 介绍所有的optim优化方法，包括公式。