数据结构与算法(java版)第二季 - 1 冒泡、选择、堆排序

初识排序

什么叫排序?

十大排序算法 

 冒泡排序(Bubble Sort)

Asserts.test(判断语句);//可以得到判断语句是否是正确的

选择排序还是有优化的空间,使用堆的方式.

选择排序的优化 - 堆数据结构

• 对下面的元素进行原地建堆

  

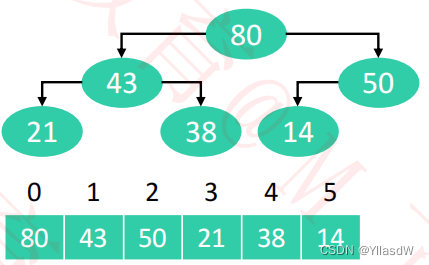
• 将堆顶元素拿出来,放到最后面,并且进行一个下滤操作,操作如下所示

  

•  重复上一步操作,直到元素0位置是最小的.
•  最好、最坏、平均时间复杂度：O(nlogn)，空间复杂度：O(1)，属于不稳定排序

原始的比较代码的写法

  protected void sort() {
        for(int end = array.length -1;end > 0;end--)
        {
            int maxIndex = array[0];
            for(int begin = 1;begin <= end;begin++)
            {
                if(array[maxIndex] <= array[begin]) //<=的原因是要使用稳定的排序算法
                {
                    maxIndex = begin;
                }
            }
            int temp = array[maxIndex];
            array[maxIndex] = array[end];
            array[end] = temp;
        }
    }

但是上述的代码在使用的过程中,交换和比较函数是可以进行提出来的,因此,可以直接进行一个类的外部声明,然后进行调用即可.

父类Sort的写出

import com.sun.xml.internal.ws.api.model.wsdl.WSDLOutput;
 
import java.util.Arrays;
 
public abstract class Sort implements Comparable{
    protected Integer[] array;
    protected int cmpCount;//进行一个比较的次数
    protected int swapCount;//进行交换的此时
    private long time;//记录执行时间
 
    public void sort(Integer[] array)
    {
        if(array == null || array.length < 2) return;
 
        this.array = array;
        long begin = System.currentTimeMillis();
        sort();
        time = System.currentTimeMillis() - begin;
    }
 
    protected abstract void sort();
 
    private String numberString(int number)
    {
        if(number < 10000) return number + " ";//注意这里是返回字符串,因此,必须要加一个" "
 
        if(number < 100000000) return number/10000.0 + "万";
 
        return number/100000000.0 + "亿";
 
    }
    /*
    返回值等于0,代表array[i1] == array[i2]
    返回值小于0,代表array[i1] < array[i2]
    返回值大于0,代表array[i1] > array[i2]
     */
    protected int cmp(int i1,int i2)
    {
        cmpCount++;
        return array[i1] - array[i2];
    }
 
    protected int cmpElements(Integer v1,Integer v2)
    {
        cmpCount++;
        return v1 - v2;
    }
 
    protected void swap(int i1,int i2)
    {
        swapCount++;
        int tmp = array[i1];
        array[i1] = array[i2];
        array[i2] = tmp;
 
    }
 
    @Override
    public String toString() {
        return "Sort{" +
                "array=" + Arrays.toString(array) +
                ", cmpCount=" + cmpCount +
                ", swapCount=" + swapCount +
                ",Consume Time =" + time/1000.000 +
                '}';
    }
 
    public int compareTo(Sort o) {
        int result = (int)(time - o.time);
        if(result != 0) return result;
 
        result = cmpCount - o.cmpCount;
        if(result != 0) return result;
 
        return swapCount - o.swapCount;
    }
}

子类SelectionSort代码是如下所示:

public class SelectionSort extends Sort{
 
    protected void sort() {
        for(int end = array.length -1;end > 0;end--)
        {
            int maxIndex = array[0];
            for(int begin = 1;begin <= end;begin++)
            {
//                if(array[maxIndex] <= array[begin]) //<=的原因是要使用稳定的排序算法
                if(cmp(maxIndex,begin) <= 0)
                {
                    maxIndex = begin;
                }
            }
//            int temp = array[maxIndex];
//            array[maxIndex] = array[end];
//            array[end] = temp;
            swap(maxIndex,end);
        }
    }
 
}

前面的BubbuleSort也是可以进行一个改正的过程,比较好理解,懒得改了.

堆排序HeapSort

public class HeapSort extends Sort{
    //1.记录堆里面的数据
    private int heapSize;
 
    protected void sort() {
        //2.原地建堆 - 将array之中的元素变成一个堆
        heapSize = array.length;
        for(int i = (heapSize >>1) -1;i >= 0;i--)
        {
            siftDown(i);
        }
        //3.交换堆顶的元素与尾部的元素
        while(heapSize > 1)
        {
            swap(0,heapSize-1);
            //4.将堆之中的数据减少
            heapSize--;
 
            //5.对0位置进行siftDown(恢复堆的性质)
            siftDown(0);
        }
 
    }
 
    /**
     * 让index位置的元素下滤
     * @param index
     */
    private void siftDown(int index) {
        Integer element = array[index];
        int half = heapSize >> 1;
        // 第一个叶子节点的索引 == 非叶子节点的数量
        // index < 第一个叶子节点的索引
        // 必须保证index位置是非叶子节点
        while (index < half) {
            // index的节点有2种情况
            // 1.只有左子节点
            // 2.同时有左右子节点
 
            // 默认为左子节点跟它进行比较
            int childIndex = (index << 1) + 1;
            Integer child = array[childIndex];
 
            // 右子节点
            int rightIndex = childIndex + 1;
 
            // 选出左右子节点最大的那个
            if (rightIndex < heapSize && cmpElements(array[rightIndex], child) > 0) {
                child = array[childIndex = rightIndex];
            }
 
            if (cmpElements(element, child) >= 0) break;
 
            // 将子节点存放到index位置
            array[index] = child;
            // 重新设置index
            index = childIndex;
        }
        array[index] = element;
    }
}