[LeetCode周赛复盘] 第 85 场双周赛20220820

一、本周周赛总结

• 前两题wa两次，哭了。
• 后两题都用了树状数组，分别IUPQ模型和PUIQ模型。
  

二、 [Easy] 6156. 得到 K 个黑块的最少涂色次数

链接: 6156. 得到 K 个黑块的最少涂色次数

1. 题目描述

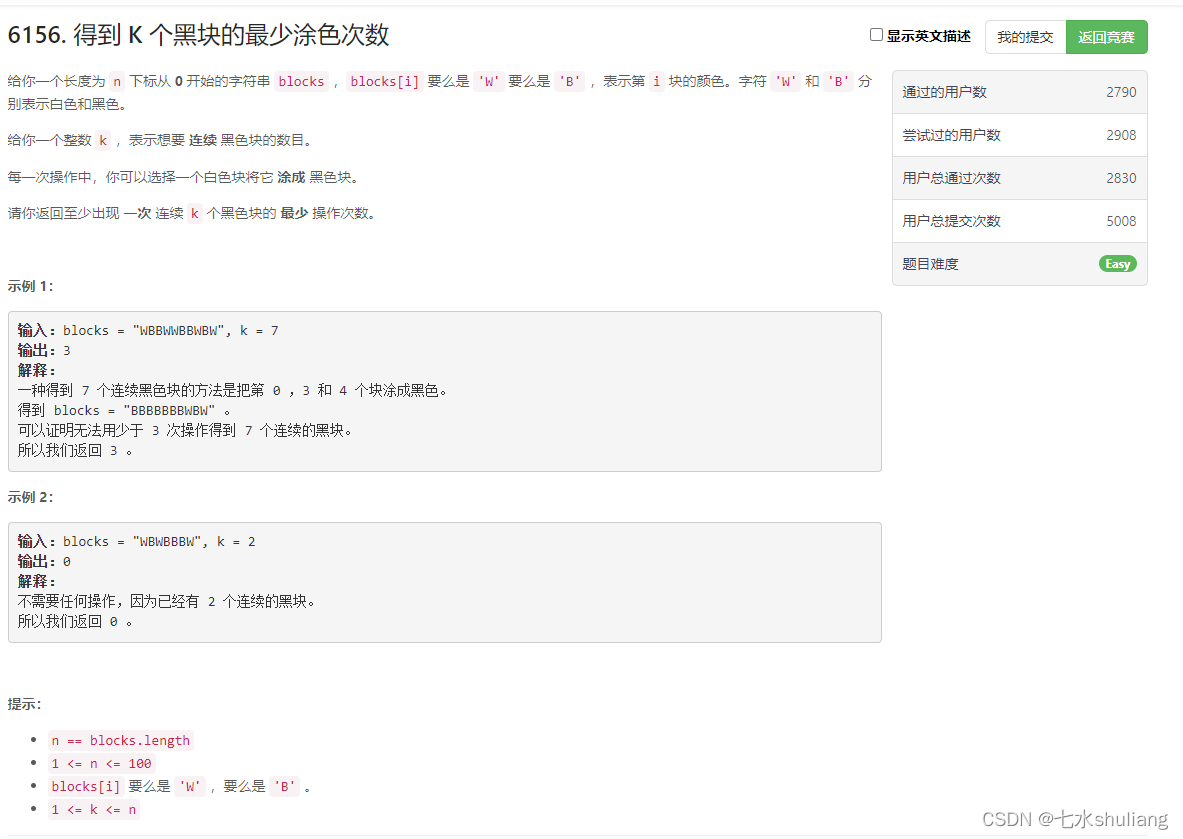
2. 思路分析

定级Easy。
一开始想前缀和浪费了很多时间，过了会发现可以直接滑窗求和减一下就可以了。

3. 代码实现

class Solution:
    def minimumRecolors(self, blocks: str, k: int) -> int:
        n = len(blocks)
        s = [(1 if x == 'B' else 0) for x in blocks ]

        x = sum(s[:k])        
        ans = k-x
        for r in range(k,n):
            l = r - k 
            x -= s[l]
            x += s[r]
            ans = min(ans,k-x)
        return ans            
1
2
3
4
5
6
7
8
9
10
11
12
13

三、[Medium] 6157. 二进制字符串重新安排顺序需要的时间

链接: 6157. 二进制字符串重新安排顺序需要的时间

1. 题目描述

2. 思路分析

定级Medium。
推规律推错了，wa一次。
然后replace暴力过的。

3. 代码实现

class Solution:
    def secondsToRemoveOccurrences(self, s: str) -> int:
        n = len(s)
        ans = 0
        t = s.replace('01','10')
        while s != t:
            s = t
            ans += 1
            t = s.replace('01','10')
        
        return ans
            
1
2
3
4
5
6
7
8
9
10
11
12

四、[Medium] 6158. 字母移位 II

链接: 6158. 字母移位 II

1. 题目描述

2. 思路分析

IQPU模型，我用了树状数组。

• shift数组实际上是告诉你哪个区间范围内的字符向前或向后共移动多少次，那累计+1或-1即可。
• 最后对每个点累计上之后对26取模转换回来即可。
• 由于是区间加，那么可以用树状数组、线段树、甚至珂朵莉。
• 但是最后要遍历每个点，因此我选了从常数最小的树状数组。

3. 代码实现

class BinIndexTree:
    def __init__(self, size):
        self.size = size
        self.bin_tree = [0 for _ in range(size+5)]
    def add(self,i,v):
        while i<=self.size :
            self.bin_tree[i] += v
            i += self.lowbit(i)
    def update(self,i,v):
        val = v - (self.sum(i)-self.sum(i-1))
        self.add(i,val)
    def sum(self,i):
        s = 0
        while i >= 1:
            s += self.bin_tree[i]
            i -= self.lowbit(i)
        return s
    def lowbit(self,x):
        return x&-x
    def _point_query(self,i):
   		return self.sum(i)
    def _interval_add(self,l,r,v):
   		self.add(l,v)
   		self.add(r+1,-v)
class Solution:
    def shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:
        bt = BinIndexTree(50000)
        for a,b,c in shifts:            
            bt._interval_add(a+1,b+1,1 if c == 1 else -1)
        abc = 'abcdefghijklmnopqrstuvwxyz'
        cba = {v:i for i,v in enumerate(abc)}
        n = len(s)
        ans = []
        for i,c in enumerate(s):
            ans.append(abc[(cba[c]+bt._point_query(i+1))%26])
        return ''.join(ans)
        
        
        
        
        
        
        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

五、[Hard] 6159. 删除操作后的最大子段和

链接: 6159. 删除操作后的最大子段和

1. 题目描述

2. 思路分析

定级Hard。
同样用了树状数组，但是用的PUIQ模型。

• 这题子段和经典的dp那道题定义不同，由于所有nums[i]>0 ，因此找0分割的连续数字段求和即可。
• 两个数组长度相同，所以题目其实是把nums中的数字全部依次删除后，求每个动作后的最大子段和，删除后的位置是空缺，切割子段用的。
• 答案的最后一个数字显然是0，因为最后要删光所有数字。
• 那么可以发现，从最后一步到第一步逆向构造是比较简单的思路。
• 一开始认为数组都是0，每加进一个数字，可能和其它数字连接上或不连，但一定构成一个新的子段，产生一个新的子段和，这个和可能是最大的；否则一定是之前跟它不连接的段最大。因此ans=max(ans,sum(cur))。
• 那我们需要快速查询添加一个位置后，它所连接的前后端点。这里其实就是找前后最近的0。那我们用一个有序集合SortedList来储存所有位置的0，当添加数字后删除这个位置的0，查询时只需lgN。
• 找到前后端点后如何计算段的和，用了树状数组。
• 为了方便的处理边界，在原数据前后都添加了一个0。我们讨论添加位置时只讨论1-n位置即可。同时树状数组使用时坐标也不用+1了。

3. 代码实现

class BinIndexTree:
    def __init__(self, size):
        self.size = size
        self.bin_tree = [0 for _ in range(size+5)]
    def add(self,i,v):
        while i<=self.size :
            self.bin_tree[i] += v
            i += self.lowbit(i)
    def update(self,i,v):
        val = v - (self.sum(i)-self.sum(i-1))
        self.add(i,val)
    def sum(self,i):
        s = 0
        while i >= 1:
            s += self.bin_tree[i]
            i -= self.lowbit(i)
        return s
    def lowbit(self,x):
        return x&-x
class Solution:
    def maximumSegmentSum(self, nums: List[int], removeQueries: List[int]) -> List[int]:
        n = len(nums)
        nums = [0]+nums+[0]
        removeQueries = [0]+removeQueries+[0]
        # a = [0]*(n+2)
        bt = BinIndexTree(n+2)
        from sortedcontainers import SortedList
        s = SortedList(range(n+2))
        ans = [0]
        for i in range(n,1,-1):
            # a[i] = removeQueries[i]
            c = removeQueries[i]+1
            bt.add(c,nums[c])
            s.remove(c)
            l = s.bisect_left(c)-1
            r = l + 1
            # print(s[l],s[r],bt.bin_tree)
            ans.append(max(ans[-1],bt.sum(s[r]-1)-bt.sum(s[l])))
        return ans[::-1]                        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39