从交叉熵到Focal Loss

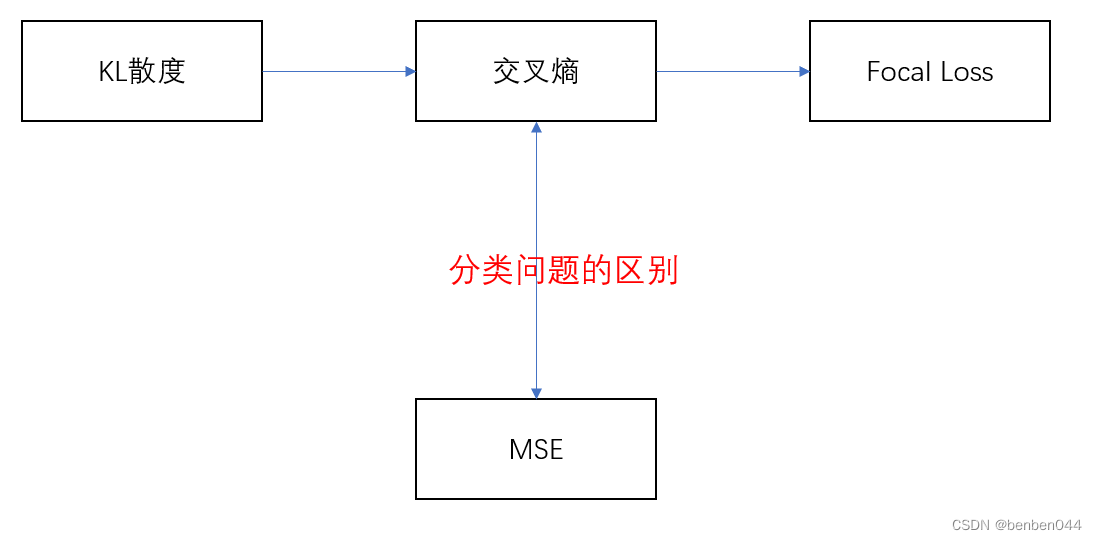
本文的主要脉络如下：

目录

1、交叉熵的由来

（1）参考：

 （2）信息量

（3）信息熵

 （4）相对熵

 （5）交叉熵由来推导

2、分类问题使用交叉熵而非MSE原因

（1）参考

（2） 交叉熵损失与均方差损失

 （3）损失函数直观理由

（4）softmax反向传播角度

3、Focal Loss

（1）参考

（2）整体理解

（3）易分辨、难分辨的含义

（4）交叉熵损失函数

 （5）样本不均衡问题

（6）平衡交叉熵函数

（7）focal loss

（8）focal loss对比平衡交叉熵

（9）focal loss的一点思考

---

1、交叉熵的由来

（1）参考：

损失函数——交叉熵由来_飞驰的拖鞋的博客-CSDN博客

交叉熵带一个”熵“字，所以必定和信息量、熵相关理论有关。 

 （2）信息量

信息量为一件事情的不确定性。概率越大，信息量越小；概率越小，信息量越大。概率和信息量成反比。

（3）信息熵

信息熵表示所有信息量的期望，是试验中每次可能结果的概率乘以其结果的综合，表达式为：

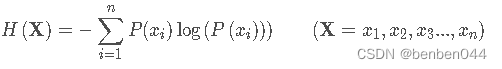
 （4）相对熵

如果对于同一个随机变量，有两个单独的概率分布P(x)和Q(x)，则我们可以使用KL散度来衡量这两个概率分布之间的差异。公式如下：

KL散度越小，表示P(x)和Q(x)越接近。

 （5）交叉熵由来推导

将KL散度公式拆开：

前者H(p(x))表示信息熵，后者为交叉熵。KL散度=交叉熵 - 信息熵。

交叉熵可以表示为：

在分类问题中，我们希望预测的分布和实际分布尽可能接近，所以应该使用KL散度公式作为损失函数。因为信息熵为p(x)的分布，p(x)为实际分布，所以该值为常量，因此只要交叉熵足够小，则KL散度足够小，因而使用交叉熵作为分类的损失函数。

2、分类问题使用交叉熵而非MSE原因

（1）参考

直观理解为什么分类问题用交叉熵损失而不用均方误差损失? - shine-lee - 博客园

分类问题为什么用交叉熵损失不用 MSE 损失_云端FFF的博客-CSDN博客_分类交叉熵 回归mse

（2） 交叉熵损失与均方差损失

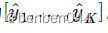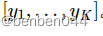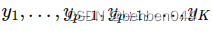假设一共有K类，令网络的输出为，对应每个类别的概率，令label为。实际结果为onehot类型，对某个属于p类的样本，令label中，其他的均为0。

对于这个样本，交叉熵为：

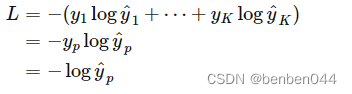
MSE为：

对比交叉熵损失与均方差损失，只看这单个样本的损失即可。

 （3）损失函数直观理由

由损失函数可见，MSE关注全部类别熵预测概率和真实概率的差；交叉熵关注的是正确类别的预测概率。

在分类问题中，对于类别之间的相关性缺乏先验知识，此时关注所有类别的预测值会给出错误的提示。比如猫、老虎、狗的3分类问题，label为[1,0,0]，在MSE看来，预测为[0.8, 0.1, 0.1]要比[0.8, 0.15, 0.05]要好，即认为平均总比倾向性要好，这个有悖于我们的常识（因为猫与老虎更接近）。

而交叉熵只关注样本所属的哪个类别，只要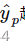越接近1就好，这个更合理。

（4）softmax反向传播角度

分类问题基本上最后通过softmax映射分布，以获得某种概率的解释。

 softmax求导见：

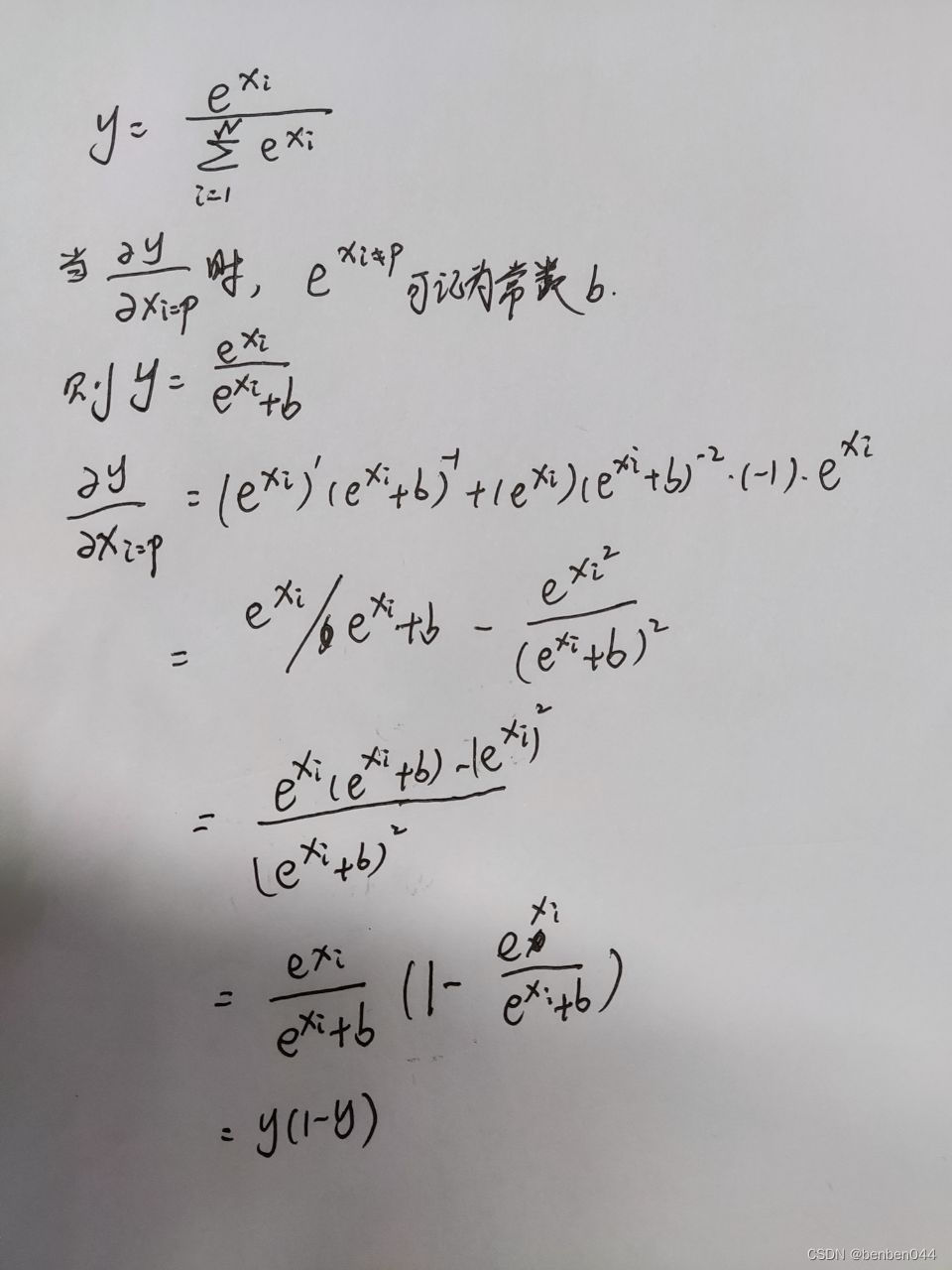
对于交叉熵：

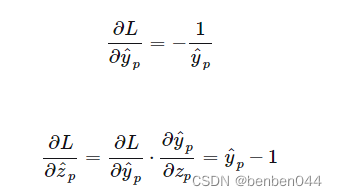
此时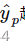越接近于1，偏导越接近于0，即分类越正确越不需要更新权重，这与期望相符。

对于MSE：

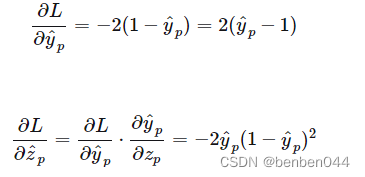
此时会出现当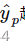=0时，分裂错误，但是不更新权重，即分类完全错误时却出现了梯度消失的问题。

3、Focal Loss

（1）参考

focal loss 通俗讲解 - 知乎

focal loss详解_为了写博客，要取一个好的名字的博客-CSDN博客_focal loss

（2）整体理解

focal loss是一种处理样本分类不均衡的损失函数。

 它侧重的点是根据样本分辨的难易程度给样本对应的损失添加权重，即给容易区分的样本添加较小的权重α1，给难分辨的样本添加较大的权重α2，损失函数的表达式为：

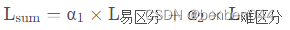
因为α2的值较大，所以损失函数的重点集中于难分辨的样本上。

（3）易分辨、难分辨的含义

这两个的区别藏在分类置信度上。

通常将分类置信度接近1的样本称为易分辨样本，其余的称之为难分辨样本。换句话说，有把握确认属性的样本称之为易分辨样本，没有把握确认属性的样本称之为难分辨样本。

（4）交叉熵损失函数

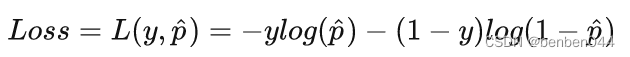
其中 为预测概率大小。

y为label，在二分类中对应0,1。

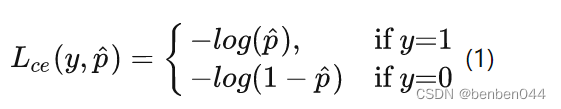
 （5）样本不均衡问题

对于所有样本，损失函数为：

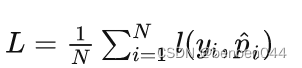
 对于二分类问题，损失函数可以写为：

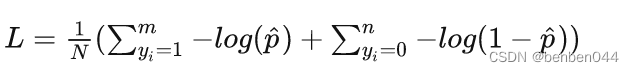
其中m为正样本个数，n为负样本个数，N为样本总数，m+n=N

当样本分布失衡时，在损失函数L的分布也会发生倾斜，如m<

（6）平衡交叉熵函数

 对于样本不平衡造成的损失函数倾斜，一个直观的做法就是在损失函数中添加权重因子，提高少数类别在损失函数中的权重，平衡损失函数的分布。比如上述二分类问题，添加权重参数后：

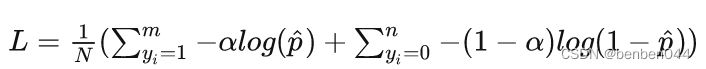
其中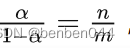， ，即权重的大小根据正负样本的分布进行设置。

（7）focal loss

focal loss也是针对样本不均衡问题提出了另外一种解决方案。

对于表达式(3)和(4)，focal loss相比交叉熵多了一个调节参数即 

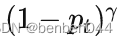
对于分类准确的样本，pt趋近于1，调节参数趋近于0.

对于分类不准确的样本呢，pt趋近于0，调节参数趋近于1.

所以相比交叉熵损失函数，focal loss对于分类不准确的样本，损失没有改变；

对于分类准确的样本，损失会变小。

整体而言，相当于增加了分类不准确样本在损失函数中的权重。

pt也反应了分类的难易程度，pt越大，说明分类的置信度越高，代表样本越易分；pt越小，分类的置信度越低，代表样本越难分。因此focal loss相当于增加了难分样本在损失函数的权重，使得损失函数倾向于难分的样本，有助于提高难分样本的准确度。针对pt为0的情况，它指的是判断某类的置信度为0，假如实际上是该类，则就变成了非常难分辨。

（8）focal loss对比平衡交叉熵

focal loss相比平衡交叉熵，两者都是试图解决样本不平衡带来的模型训练问题。后者从样本分布角度对损失函数添加权重因子，前者从样本分类难易程度出发，使loss聚焦于难分样本。

focal loss为什么有效？样本非平衡造成的问题就是样本数少的类别分类难度较高。因此从样本难易分类角度出发，使得loss聚焦于难分样本，解决样本少的类别分类准确率不高的问题，也就是focal loss解决了样本非平衡的问题。

（9）focal loss的一点思考

难分类样本与易分类样本其实是一个动态概念，也就是说pt会随着训练过程而变化。原先易分类样本即pt大的样本，可能随着训练过程变化为难训练样本即pt小的样本。

在loss梯度中，难训练样本起主导作用，即参数的变化主要是朝着优化难训练样本的方向改变。当参数变化后，可能会使原先易训练的样本pt发生变化，即可能变为难训练样本。当这种情况发生时，可能会造成模型收敛速度慢。

为了防止难易样本的频繁变化，应当选取小的学习率，防止学习率过大，造成w变化较大从而引起pt的巨大变化，造成难易样本的改变。