LeetCode 热题 HOT 100 第七十八天 406. 根据身高重建队列 中等题 用python3求解

题目地址

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：
输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例 2：
输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

提示：
1 <= people.length <= 2000
0 <= hi <= 10^6
0 <= ki < people.length
题目数据确保队列可以被重建

解法：先排序，再插队
参考：指路

解题思路:
题目描述：整数对 (h, k) 表示，其中 h 是这个人的身高，k 是排在这个人前面且身高大于或等于 h 的人数。

一般这种数对，还涉及排序的，根据第一个元素正向排序，根据第二个元素反向排序，或者根据第一个元素反向排序，根据第二个元素正向排序，往往能够简化解题过程。

在本题目中，我首先对数对进行排序，按照数对的元素 1 降序排序，按照数对的元素 2 升序排序。原因是，按照元素 1 进行降序排序，对于每个元素，在其之前的元素的个数，就是大于等于他的元素的数量，而按照第二个元素正向排序，我们希望 k 大的尽量在后面，减少插入操作的次数。

图解：

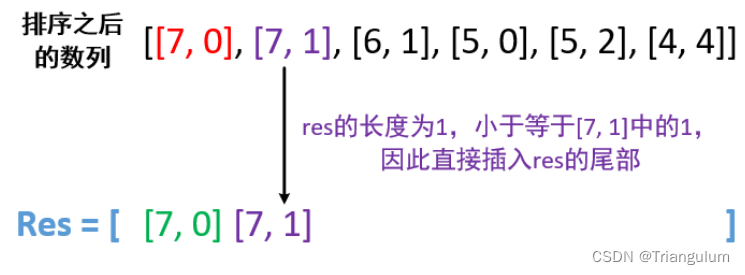
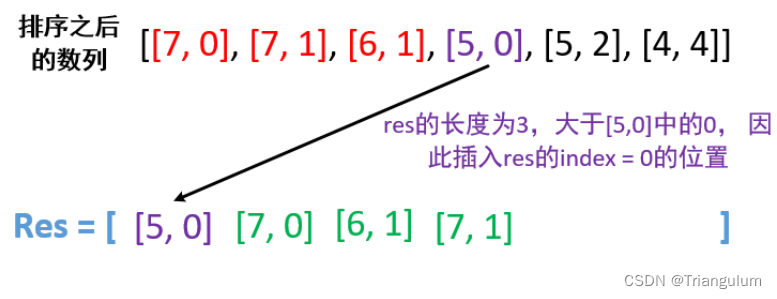
代码实现：
法一：for 循环实现，额外 res 数组空间存储
如果题目没有要求一定要在原数组上修改，或者要求一定不能在原数组上进行修改，那么可以用for循环实现。
但由于多了个res数组，会占据一定的空间存储。

class Solution:
    def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
        res = []
        people = sorted(people, key = lambda x: (-x[0], x[1]))
        for p in people:
            if len(res) <= p[1]:
                res.append(p)
            elif len(res) > p[1]:
                res.insert(p[1], p)
        return res

1
2
3
4
5
6
7
8
9
10
11

法二：while 循环实现，原地改变
同理，如果题目要求一定要在原数组上修改，或者没有要求一定不能在原数组上进行修改，那么可以用while循环实现。
由于while循环是在原来的people数组上进行操作，不会由额外数组的产生，所以占据的存储空间会比用for循环实现要少。

class Solution:
    def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
        people = sorted(people, key = lambda x: (-x[0], x[1]))
        i = 0
        while i < len(people):
            if i > people[i][1]:
                people.insert(people[i][1], people[i])
                people.pop(i+1)
            i += 1
        return people

1
2
3
4
5
6
7
8
9
10
11