OpenCV图像处理学习十七，Canny边缘检测算法实现

一.Canny 边缘检测算法的诞生

提取图片的边缘信息是底层数字图像处理的基本任务之一。边缘信息对进一步提取高层语义信息有很大的影响。Canny 边缘检测算法 是 John F. Canny 于 1986年开发出来的一个多级边缘检测算法，至今仍然是边缘检测的最优算法, 最优边缘检测的三个主要评价标准是:

低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报。
高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。
最小响应: 图像中的边缘只能标识一次。

=================================================================

二.Canny 边缘检测算法

（1）使用高斯平滑滤波器卷积处理图像，降噪消除噪声，平滑图像

#API 函数接口
GaussianBlur(Mat src,Mat dst,Size(w,h),sigmax,sigmay)
//参数说明
src：输入源图像
dst：目标图像
Size(w,h) : 要使用的内核的大小。w 和H必须是奇数和正数，否则将使用σX和σÿ参数计算大小。
sigmax : x中的标准差。写0表示使用内核大小计算σx
sigmay : y的标准差。写0表示使用内核大小计算σy。

（2）计算图像的梯度大小和方向

计算梯度幅值和方向可选用soble算子、Prewitt算子、Roberts算子模板等等.这样就可以得图像在X和Y方向梯度大小，求出总的图像梯度G,并且有X和Y方向上的梯度分量就可以求出梯度方向θ的大小，从而的到图像的边缘方向（边缘方向总是垂直于梯度方向)。

Sorbel算子X和Y方向的图像梯度分别为:

---------------------------------------------------------------------------------------------------------------------------------

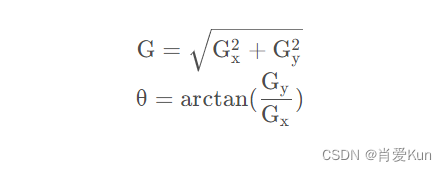
第一是通过Sorbel算子X和Y方向的图像梯度可以判断

在待处理的图像中，C是需要判断梯度方向的像素，梯度方向一般都划分为4类，其反方向由于关于中心对称，因此也属于同一方向。分别为水平（0°），45°，垂直（90°）和135°这四个方向，有图像梯度的计算公式   θ  =  arctan(Gy/Gx) 可以得出θ角度的值，再通过该θ值属于哪个区间范围把图像梯度量化到某一个方向上。

将各点的梯度方向近似/量化到0°、90°、45°、135°四个梯度方向上进行,每个像素点梯度方向按照距离这四个方向的相近程度，用这四个方向来代替。通过量化，意味着图像中各点的梯度方向只能沿着0°、90°、45°、135°四个方向中的某一个。

•  图像水平边缘——梯度方向为垂直： 
•  图像135°边缘——梯度方向为45°：                             
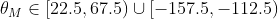
•  图像垂直边缘——梯度方向为水平：                            
•  图像45°边缘——梯度方向为135°：                               

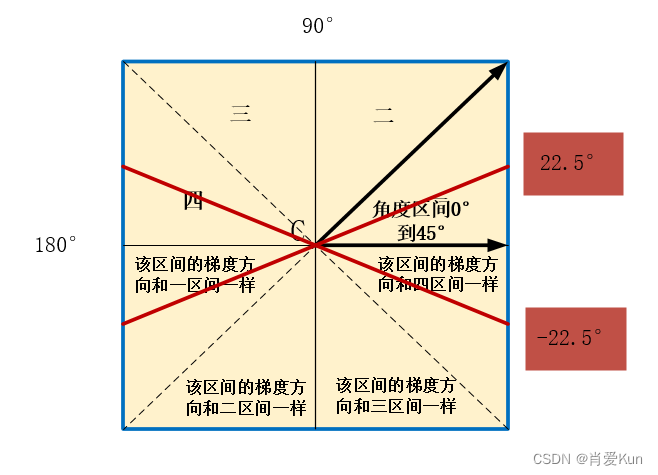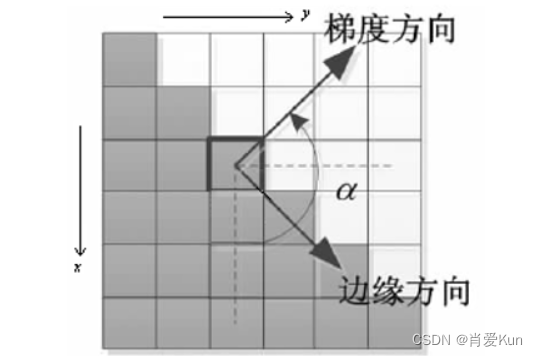
梯度方向划分如上图所示：

当计算出来的角度θ的值位于22.5°和-22.5°红色线夹角区域时，此时最接近于0°，所以图像梯度被量化为 0°，图像边缘的角度为垂直90°。边缘方向总是垂直于梯度方向，如下图所示，下图的梯度方向为45°，边缘方向为135°。

=================================================================

（3）图像非极大值抑制

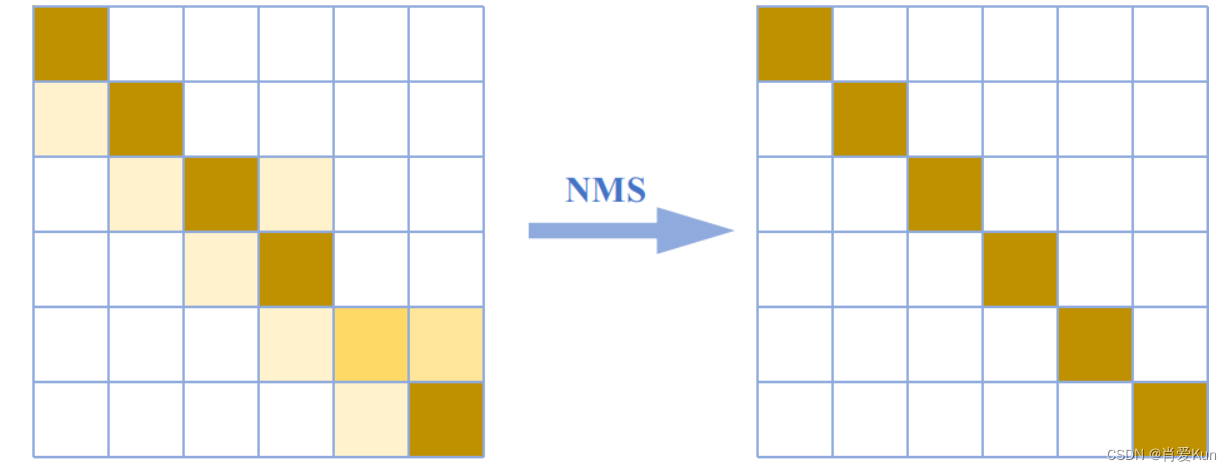
非极大值抑制（Non-Maximum Suppression，NMS）： 抑制不是极大值的元素，可以理解为局部最大搜索。保留局部最大值，抑制非局部最大值的所有值。

图像像素最大值在图像梯度方向上时

在每一点上，领域中心像素与沿着其对应的图像梯度方向的两个像素相比，若中心像素为最大值，则保留下来；否则中心像素置0，这样可以抑制非极大值，保留局部梯度最大的点，以得到细化的边缘。 非极大值抑制的目的在于细化边缘，将原有粗略边缘检测图中的宽边细化为真正的边缘，从而可以更好的凸显物体的轮廓。非极大抑制是一种瘦边经典算法。它抑制那些梯度不够大的像素点，只保留最大的梯度，从而达到瘦边的目的。

重点：Canny中的非极大值抑制是沿着图像梯度方向对幅值进行非极大值抑制，而非边缘方向。

图像梯度方向并非特定角度（0°，45°，90°，135°）时，采用线性插值的方法来求取

在上图中，C是中心像素点，A1、A2、A3、A4都代表在图像梯度上的像素点，红色的直线是它的梯度方向，并不在0°，45°，90°和135°的图像梯度上，如果判断C是否为局部极大值，需要比较梯度幅值C和直线与g1g2和g2g3的交点处的dtmp1和dtmp2处的梯度幅值的大小关系。但是dtmp1和dtmp2不是整像素，而是亚像素点，也就是坐标是浮点的，这时就要利用线性插值求取。

写个线性插值的公式：设1的幅值M(A1)，A2的幅值M(A2),则dtmp1可以得到：
 M(dTmp1)=w*M(A2)+(1-w)*M(A1)  ;
其中w=distance(dTmp1,A2)/distance(A1,A2) ;distance(A1,A2) 表示两点之间的距离。实际上w是一个比例系数，这个比例系数可以通过梯度方向(幅角的正切和余切)得到。

=========================================================================

（4）滞后阈值处理

滞后阈值处理是为了清除由于噪声和颜色变化引起的一些边缘像素，这时必须用弱梯度值过滤边缘像素,并保留具有高梯度值的边缘像素,可以通过选择高低阈值来实现。

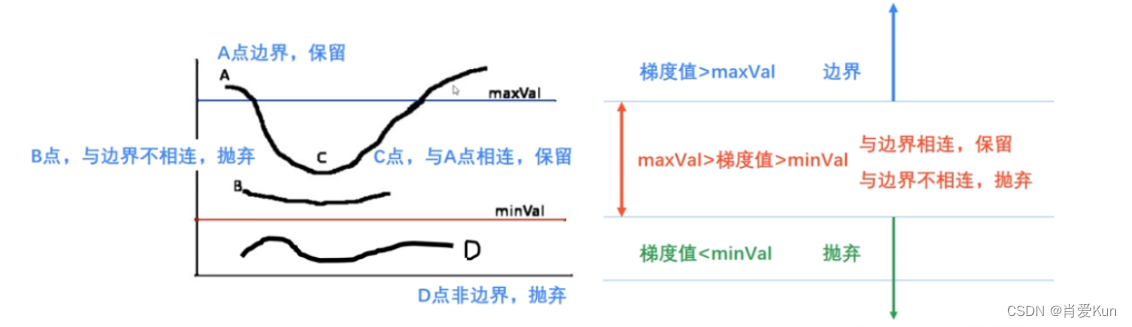
用双阈值算法检测和连接边缘像素，选取高阈值和低阈值系数TH和TL，比率为2:1或3:1。（一般取TH=0.3或0.2,TL=0.1）；将小于低阈值的像素点抛弃，赋值为0；将大于高阈值的像素点立即标记（这些点为确定边缘点），赋1或255；将小于高阈值，大于低阈值的点使用8连通区域确定（即：只有与TH像素连接时才会被接受，成为边缘点，赋 1或255）；通过滞后阈值(双阈值)能够减少伪边缘,同时对真正的边缘进行连接.如下为滞后阈值示意图,经过滞后阈值后,存在缝隙的边缘被连接起来。

=========================================================================

三.Canny边缘检测API函数接口

#Canny边缘检测API
cv::Canny（ 
        InputArray src,    // 8-bit的输入图像 
        OutputArray edges, // 输出边缘图像， 一般都是二值图像，背景是黑色 
        double threshold1, // 低阈值，常取高阈值的1/2或者1/3 
        double threshold2, // 高阈值 
        int aptertureSize, // Soble算子的size，通常3x3，取值3 
        bool L2gradient    // 选择 true表示是L2来归一化，否则用L1归一化 
）

=========================================================================

代码实现

#include <opencv2/opencv.hpp>
#include <iostream>
#include <math.h>
 
using namespace cv;
Mat src, gray_src, dst;
int t1_value = 10;
int max_value = 255;
const char* OUTPUT_TITLE = "Canny Result";
void Canny_Demo(int, void*);
int main(int argc, char** argv) {
	src = imread("D:/vcprojects/images/lena.png");
	if (!src.data) {
		printf("could not load image...\n");
		return -1;
	}
 
	char INPUT_TITLE[] = "input image";
	namedWindow(INPUT_TITLE, CV_WINDOW_AUTOSIZE);
	namedWindow(OUTPUT_TITLE, CV_WINDOW_AUTOSIZE);
	imshow(INPUT_TITLE, src);
 
	cvtColor(src, gray_src, CV_BGR2GRAY);
	createTrackbar("Threshold Value:", OUTPUT_TITLE, &t1_value, max_value, Canny_Demo);
	Canny_Demo(0, 0);
 
	waitKey(0);
	return 0;
}
 
void Canny_Demo(int, void*) {
	Mat edge_output;
	blur(gray_src, gray_src, Size(3, 3), Point(-1, -1), BORDER_DEFAULT);
	Canny(gray_src, edge_output, t1_value, t1_value * 2, 3, false);
 
	//dst.create(src.size(), src.type());
	//src.copyTo(dst, edge_output);
	// (edge_output, edge_output);
	imshow(OUTPUT_TITLE, ~edge_output);
}

---------------------------------------------------------------------------------------------------------------------------------

代码中设置高阈值和低阈值系数TH和TL比例为2:1，设置高阈值为255.低阈值为10

图像处理效果

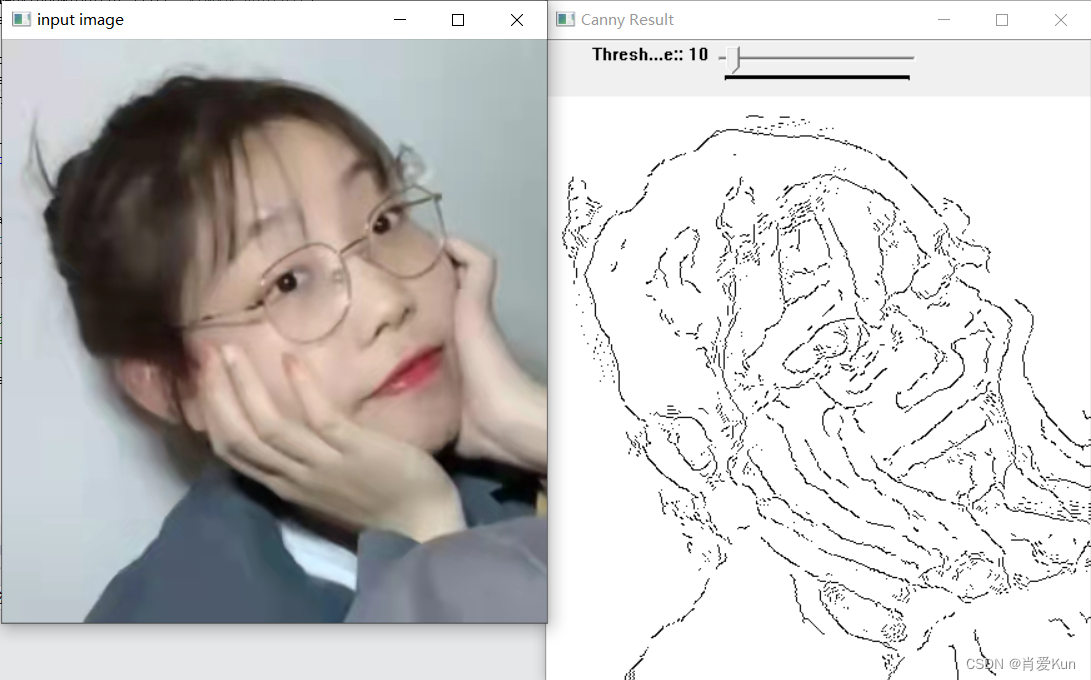
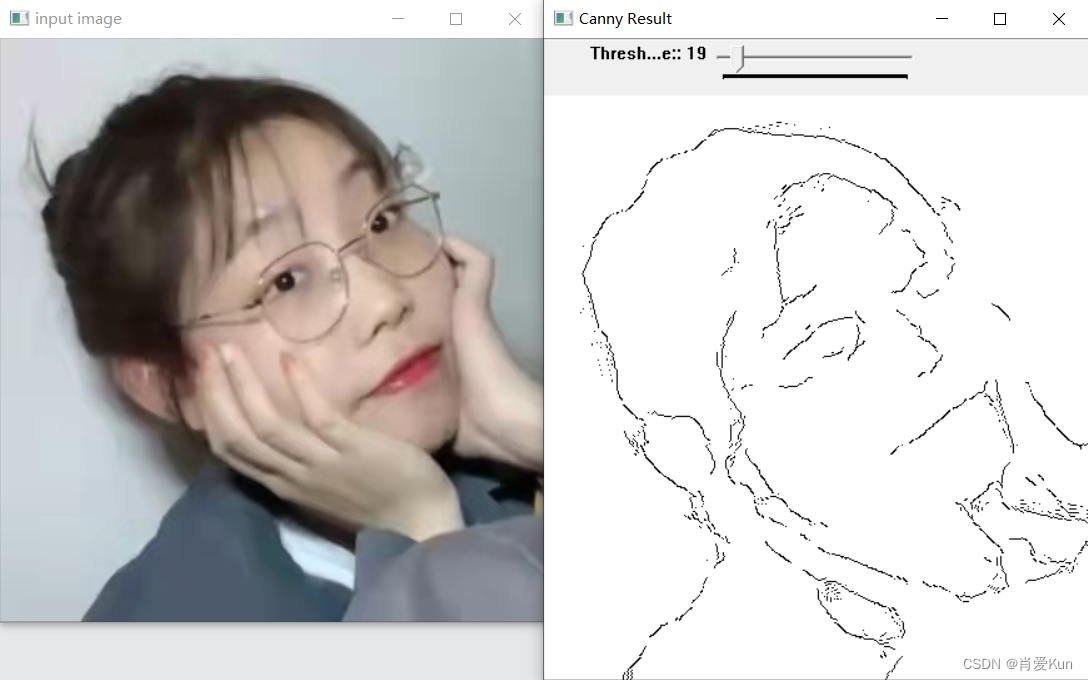
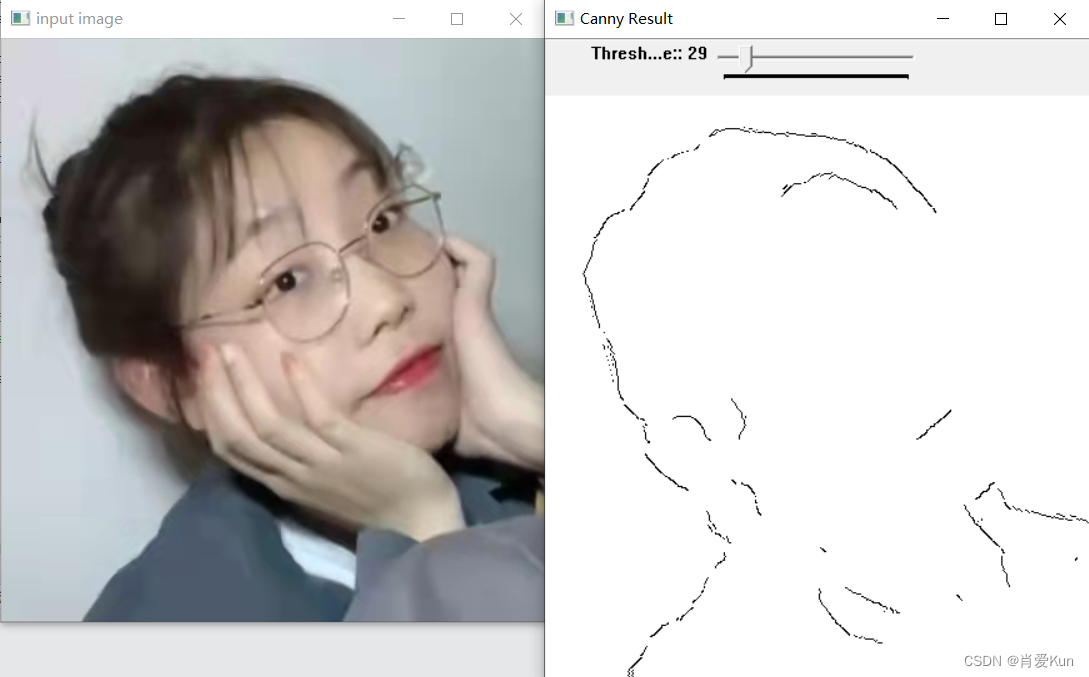
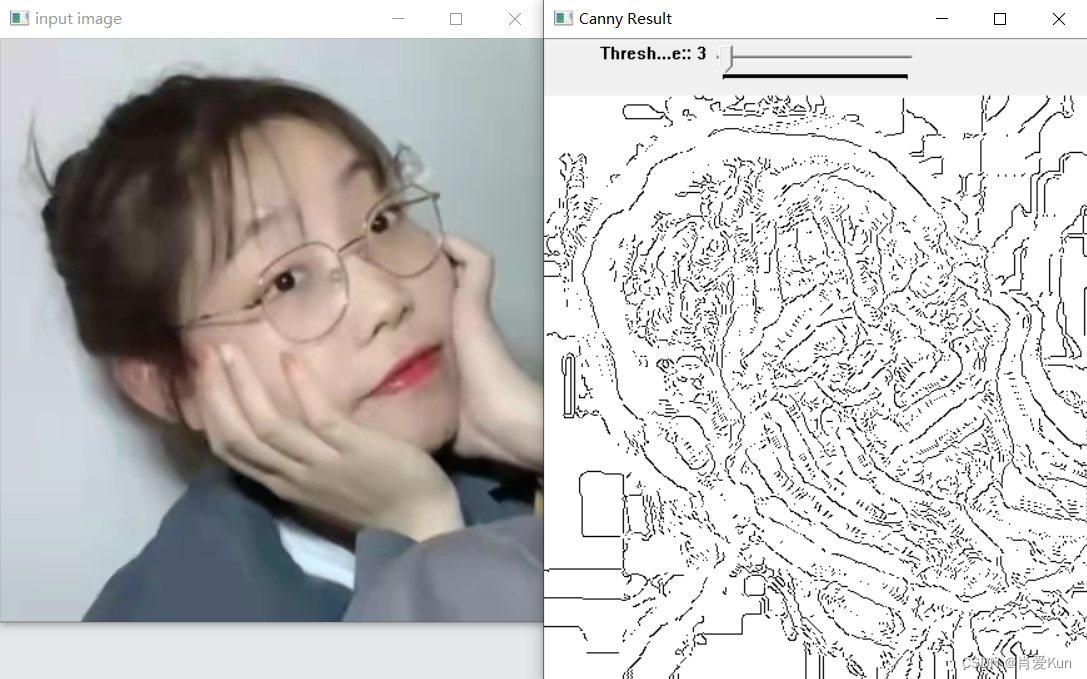
 可以看到，最低阈值设置的越高，被排除过滤的像素就越多，不连续的像素就越少，图像就越简单。