机器学习之决策树

决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。

一、绪论

我们还使用覆盖算法的例子：

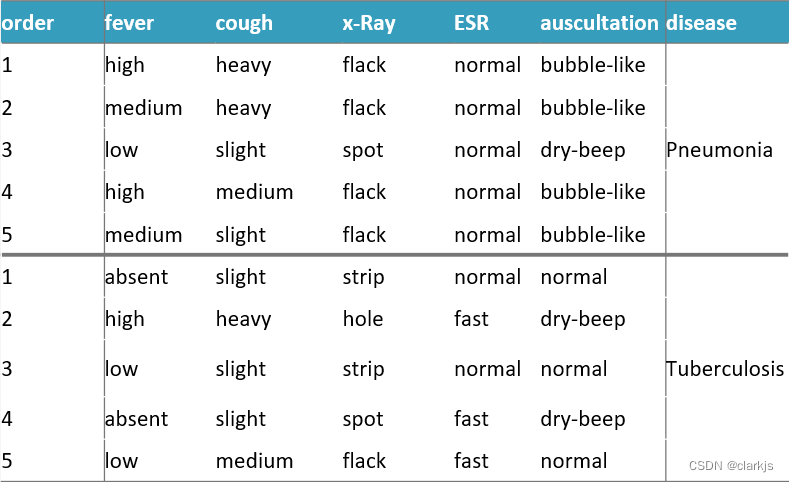
根据正例和反例，尝试构建决策树，使得我们可以区分正例和反例，随便举两个例子👇：

可见：使用不同特征作为根节点，决策树的大小及搜索时间有很大差异，因此选取合适的特征构造决策树很重要。 因此，使用不同的属性次序来建立分类树，其规模是不同的，分类效率也不同 那么，如果选择分类器中使用的属性次序，才能构造规模最小的树？这是决策树的核心问题。

二、决策树算法介绍

1. 熵与信息熵

熵 —— 表示系统的混乱程度，和高中化学中的熵差不多是一个意思。

2. ID3算法

（1）公式

一个好的分类属性讲使得信息增益最大，因此我们每次选取信息增益值gain最大的属性进行分类。

（2） 举例（还是前面的例子）

上面的计算过程以计算gain(x5)为例，当然我们要把x1,x2,x3,x4,x5的gain都计算出来，然后取最大的，可以算出，gain（x5）最大，然后以x5为根画出决策树，👇

在尚未分类结束的例子子集{3+，2-，4-}中，重复以上计算，可以计算出gain（x1）=gain（x4）并且最大，使用x4属性继续分类，即可得到如下分类树：

注：（1）信息熵分类的本质是启发式贪心算法；（2）生成最小规模的决策树是NP问题

3. 评价矩阵算法

和FCV算法一样，先分别建立正例集和反例集的评价矩阵，这里没看懂的话建议参考覆盖算法的博客：https://blog.csdn.net/m0_51339444/article/details/126435474
建立评价矩阵后，利用公式：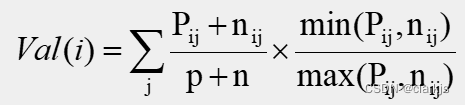
取Val（i）最小值，选取第i个属性作为分类树的节点。还是以x5为例，计算方法如下：

4. C5.0算法

博主认为C5.0和ID3几乎一样，没看出来有什么区别，要是有大佬知道有什么区别，希望能私我以下，十分感谢~