刘二大人 PyTorch深度学习实践 笔记 P7 处理多维特征的输入

P7 处理多维特征的输入

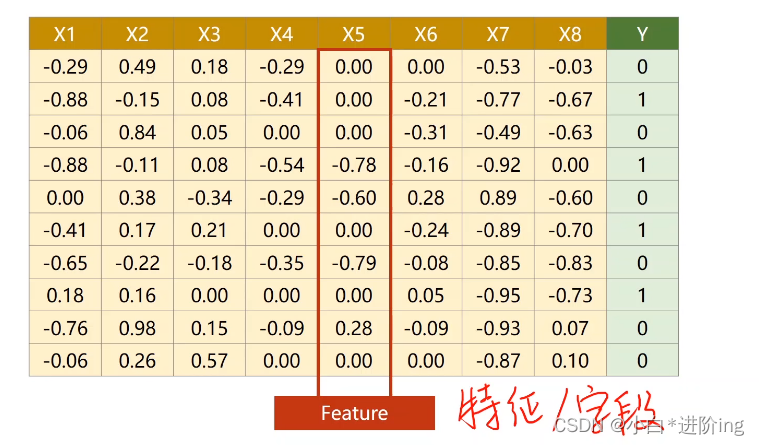
1、行为记录，列为特征

2、Anaconda3 数据存储路径

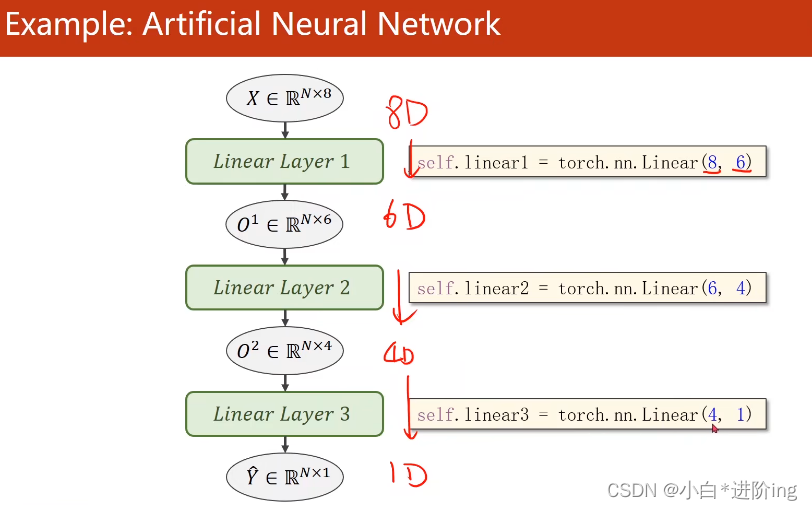
3、转化

转化成矩阵向量化的计算，可以利用CPU等进行并行计算，提高计算的速度

一般来说，中间层数越多，网络对非线性映射的拟合程度越好，学习能力越强，但是学习能力太强可能会将输入的噪声也学习进去，所以网络学习能力太强也不好，学习应该具有泛化能力。

|:😐 学习新知识，提高泛化能力——学会读文档+计算机系统基本架构理解

4、代码实现：

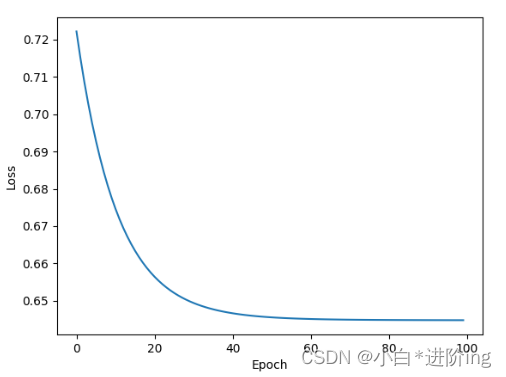
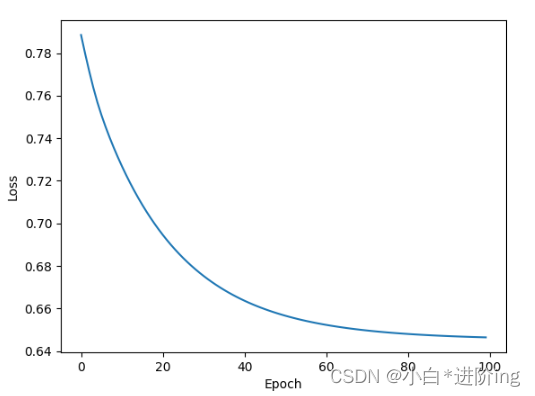
import numpy as np
import torch
import matplotlib.pyplot as plt

# gz压缩包里的文件名一样，就可以用loadtxt把数据读出来
# delimiter=',' , 以逗号作为分隔符
# dtype=np.float32 , 数据类型为32位的浮点数
xy = np.loadtxt('dataset/diabetes.csv.gz', delimiter=',', dtype=np.float32)

# 该函数会创建两个tensor张量出来
x_data = torch.from_numpy(xy[:, :-1]) # 所有行，除了最后一列
y_data = torch.from_numpy(xy[:, [-1]]) # 所有行，最后一列 转为矩阵而不是向量

class Model(torch.nn.Module):
	def __init__(self):
		super(Model, self).__init__()
		self.linear1 = torch.nn.Linear(8, 6) # 第一层是8维到6维的非线性空间变换
		self.linear2 = torch.nn.Linear(6, 4) # 第二层是6维到4维的非线性空间变换
		self.linear3 = torch.nn.Linear(4, 1) # 第三层是4维到1维的非线性空间变换
		self.sigmoid = torch.nn.Sigmoid() # 作为一个运算模块

	def forward(self, x):
		x = self.sigmoid(self.linear1(x))
		x = self.sigmoid(self.linear2(x))
		x = self.sigmoid(self.linear3(x))
		return x

model = Model()

criterion = torch.nn.BCELoss(reduction='mean') # loss均值
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

epoch_list = []
loss_list = []

for epoch in range(100):
	y_pred = model(x_data) # 并没有做mini-batch
	loss = criterion(y_pred, y_data)
	print(epoch, loss.item())
	epoch_list.append(epoch)
	loss_list.append(loss.item())

	optimizer.zero_grad()
	loss.backward()

	optimizer.step()


plt.plot(epoch_list, loss_list)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

输出：

0 0.7222060561180115
1 0.7151467800140381
2 0.708731472492218
3 0.7029024958610535
4 0.697607159614563
5 0.6927972435951233
6 0.6884285807609558
7 0.6844607591629028
8 0.6808571219444275
9 0.6775842308998108
10 0.6746116876602173
11 0.6719117164611816
12 0.6694590449333191
13 0.6672309637069702
14 0.6652066707611084
15 0.6633674502372742
16 0.6616960167884827
17 0.6601769924163818
18 0.6587962508201599
19 0.657541036605835
20 0.6563997864723206
21 0.655362069606781
22 0.6544182300567627
23 0.6535598039627075
24 0.6527788639068604
25 0.6520683765411377
26 0.6514217257499695
27 0.6508333683013916
28 0.6502977609634399
29 0.649810254573822
30 0.6493661999702454
31 0.6489620804786682
32 0.6485939025878906
33 0.6482585668563843
34 0.6479530930519104
35 0.6476748585700989
36 0.6474213600158691
37 0.6471902132034302
38 0.646979570388794
39 0.6467875838279724
40 0.6466125249862671
41 0.6464529037475586
42 0.6463074088096619
43 0.6461746692657471
44 0.6460535526275635
45 0.6459430456161499
46 0.6458422541618347
47 0.6457502841949463
48 0.6456663608551025
49 0.6455896496772766
50 0.6455196738243103
51 0.6454557776451111
52 0.645397424697876
53 0.6453441381454468
54 0.6452954411506653
55 0.6452507972717285
56 0.6452100872993469
57 0.6451728940010071
58 0.6451389193534851
59 0.6451077461242676
60 0.6450792551040649
61 0.6450531482696533
62 0.6450293064117432
63 0.645007312297821
64 0.6449873447418213
65 0.6449688673019409
66 0.6449519991874695
67 0.6449365615844727
68 0.6449223160743713
69 0.6449092626571655
70 0.6448972225189209
71 0.644886314868927
72 0.6448760628700256
73 0.6448667049407959
74 0.6448581218719482
75 0.6448501348495483
76 0.644842803478241
77 0.6448360085487366
78 0.6448296904563904
79 0.6448239088058472
80 0.6448184251785278
81 0.6448134183883667
82 0.6448087096214294
83 0.6448043584823608
84 0.6448003053665161
85 0.6447965502738953
86 0.6447930335998535
87 0.6447896361351013
88 0.6447865962982178
89 0.644783616065979
90 0.6447808146476746
91 0.6447781920433044
92 0.6447756886482239
93 0.6447734832763672
94 0.644771158695221
95 0.6447690725326538
96 0.6447670459747314
97 0.6447651386260986
98 0.6447632908821106
99 0.6447615027427673
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

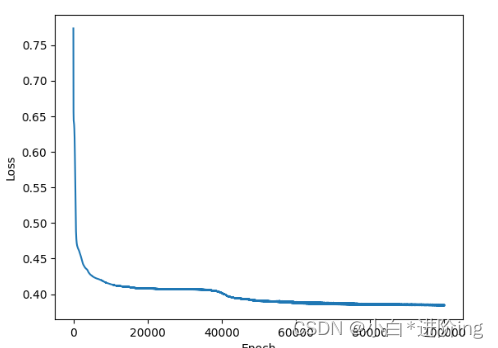
将训练次数提升，精确度明显提升了

for epoch in range(100000):
	y_pred = model(x_data) # 并没有做mini-batch
	loss = criterion(y_pred, y_data)
	# print(epoch, loss.item())
	epoch_list.append(epoch)
	loss_list.append(loss.item())

	optimizer.zero_grad()
	loss.backward()

	optimizer.step()

	if epoch % 100 == 0:
		# 三目运算
		y_pred_label = torch.where(y_pred >= 0.5, torch.tensor([1.0]), torch.tensor([0.0]))
		# 计算精确度
		acc = metrics.accuracy_score(y_pred_label, y_data, normalize=True)
		print("loss = ", loss.item(), "acc = ", acc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

输出：

...
loss =  0.3848259449005127 acc =  0.8287220026350461
loss =  0.3847823441028595 acc =  0.8287220026350461
loss =  0.38398289680480957 acc =  0.8326745718050066
1
2
3
4

5、练习

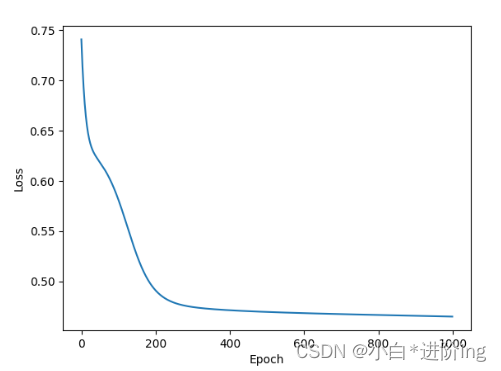
只需要修改如下代码即可

class Model(torch.nn.Module):
	def __init__(self):
		super(Model, self).__init__()
		self.linear1 = torch.nn.Linear(8, 6)
		self.linear2 = torch.nn.Linear(6, 4)
		self.linear3 = torch.nn.Linear(4, 1)
		self.sigmoid = torch.nn.Sigmoid() # 作为一个运算模块
		self.relu = torch.nn.ReLU() # 作为一个运算模块

	def forward(self, x):
		x = self.relu(self.linear1(x))
		x = self.relu(self.linear2(x))
		x = self.sigmoid(self.linear3(x))
		return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14

输出：

0 0.7885610461235046
1 0.7797487378120422
2 0.7715118527412415
3 0.7638062238693237
4 0.7568893432617188
5 0.750842809677124
6 0.7453811764717102
7 0.7403252720832825
8 0.7355858683586121
9 0.7311105728149414
10 0.726868212223053
...
90 0.6470083594322205
91 0.6469311714172363
92 0.6468574404716492
93 0.6467872262001038
94 0.6467201113700867
95 0.6466561555862427
96 0.6465951204299927
97 0.6465367674827576
98 0.6464811563491821
99 0.646428108215332
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

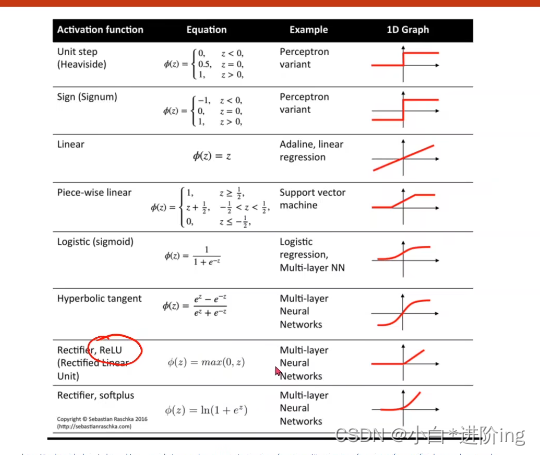
Tanh函数

其他大同小异，略，请自行测试。