图解LeetCode——654. 最大二叉树（难度：中等）

一、题目

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1> 创建一个根节点，其值为 nums 中的最大值。
2> 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3> 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。 

二、示例

2.1> 示例 1：

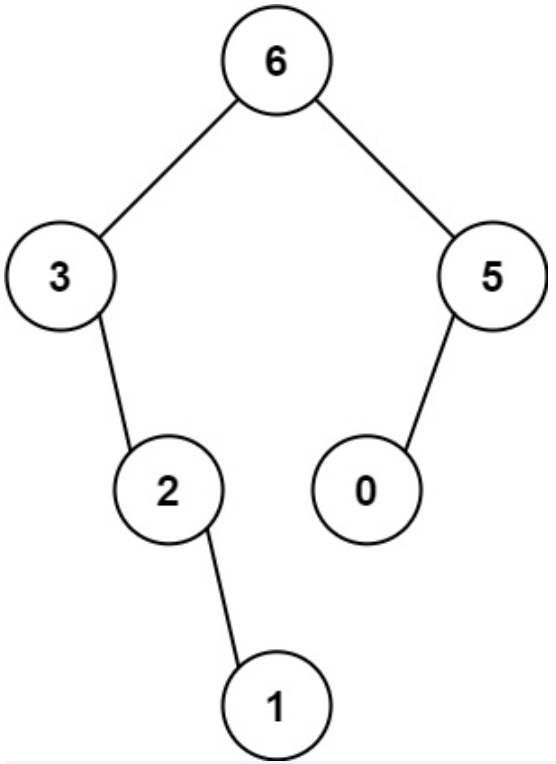
【输入】nums = [3,2,1,6,0,5]
【输出】[6,3,5,null,2,0,null,null,1]
【解释】递归调用如下所示：

• [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5]
• [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1]
• 空数组，无子节点
• [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1]
• 空数组，无子节点
• 只有一个元素，所以子节点是一个值为 1 的节点
• [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 []
• 只有一个元素，所以子节点是一个值为 0 的节点
• 空数组，无子节点

2.2> 示例 2：

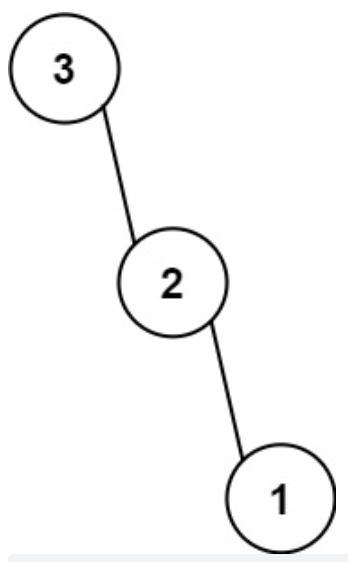
【输入】nums = [3,2,1]
【输出】[3,null,2,null,1]

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• nums 中的所有整数 互不相同

三、解题思路

3.1> 思路1：递归

根据题目描述，我们很容易会想到通过递归的方式对本题进行解答。因为无论是拆分出来左子数组还是右子数组，那么对于子数组的操作，依然都是一样的逻辑。所以，初步思路上面，我们首先确定以递归的方式进行解题。

其次，由于是需要以当前数组的最大值对数组进行“分割”，那么我们可以提供一个通用的方法，即：int maxElementIndex(int[] nums, int startIndex, int endIndex)，获取数组nums在[startIndex，endIndex]范围内的最大元素值，作为返回值进行返回。当然，我们这里采用的是根据指定开始下标（startIndex）和结束下标（endIndex）来确定最大值所在范围的，也可以采取Arrays.copyOfRange(...)方法，来获取一个全新的子串，只是这种操作对于代码执行的效率上，会有一定的影响。

语言描述比较生涩，我们依然采用举例方式进行讲解。假设我们需要处理的数组为nums = [3,2,1,6,0,5]，那么首先，获得最大值为6，创建一个新的树节点Node(6)，并划分左子数组[3,2,1]和右子数组[0,5]。在左子数组[3,2,1]中，最大值为3，创建新的树节点Node(3)，并作为Node(6)的左子树；在右子数组[0,5]中，最大值为3，创建新的节点Node(5)，并作为Node(6)的右子树。下面逻辑以此类推，具体详细步骤，请参照下图：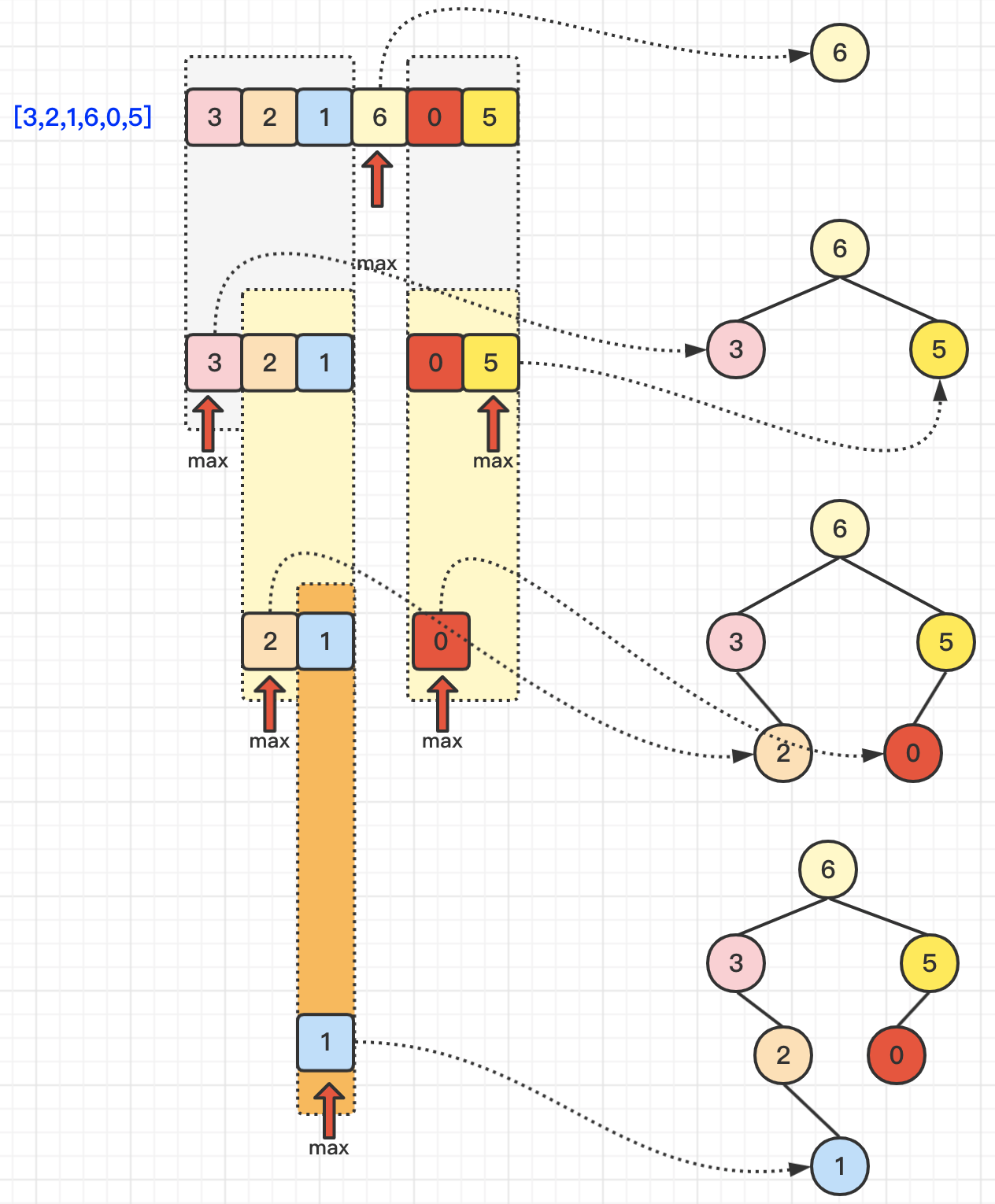

针对于递归和数组分割的方式对题目进行解答，这个思路其实于题目描述的操作方式一样，所以，思路不难。具体实现，请参照 4.1> 实现1：递归

3.2> 思路2：单调栈

我们我们通过递归操作的时候，会发现虽然每次都对数组进行了拆分操作，但是，对数组中的元素也会进行多次的重复遍历，那么有没有一种方式，可以仅通过对数组nums的一次遍历，就可以得出最终结果的呢？ 其实有的，我们可以通过单调栈的方式进行操作。

采用单调栈的基本思路是这样的：

1> 如果栈顶元素大于待插入的元素，那么直接入栈。
2> 如果栈顶元素小于待插入的元素，那么栈顶元素出栈。

当然，在对比两个节点大小和出入栈的同时，依然还是会根据题意，进行二叉树的构造。即：

1> 如果栈顶元素大于待插入的元素，则：栈顶元素.right = 待插入元素。
2> 如果栈顶元素小于待插入的元素，则：待插入元素.left = 栈顶元素。

我们依然以nums = [3,2,1,6,0,5]为例，看一下通过单调栈是怎么创建二叉树的。首先，对于数组中的前三个元素，满足Node(3) > Node(2) > Node(1)，所以，这三个元素直接入栈，并且构造二叉树Node(3).right = Node(2); Node(2).right = Node(1)；具体操作，如下图所示：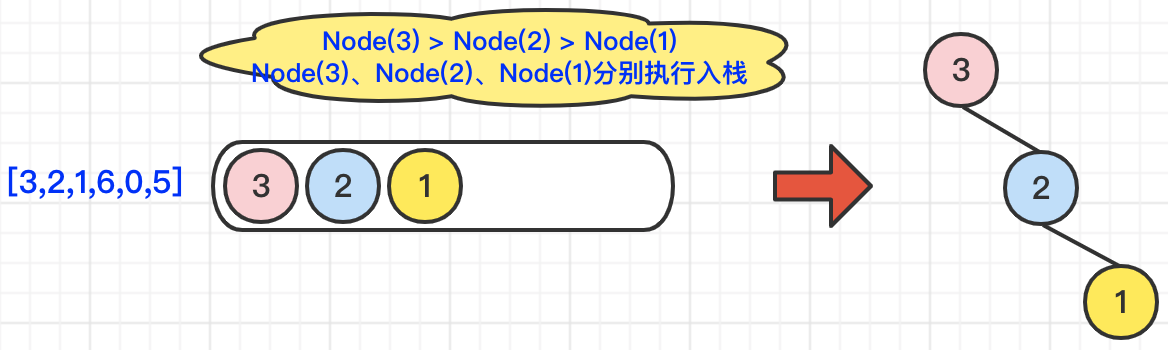

当我们遍历到Node(6)的时候，由于Node(1)小于Node(6)，所以Node(1)出栈，并且执行Node(6).left = Node(1); 又由于Node(2) 也小于Node(6)，所以Node(2)也执行出栈操作，并执行并且执行Node(6).left = Node(2);注意：此时Node(6) 的左子树节点从Node(1)变为了Node(2);由于Node(3)也小于Node(6)，Node(3)也执行出栈操作，并执行并且执行Node(6).left = Node(3);注意：此时Node(6) 的左子树节点从Node(2)变为了Node(3);由于栈中元素都出栈了，没有可以跟Node(6)进行对比的元素了，所以，此时Node(6)入栈，本次操作完毕。具体操作，如下图所示：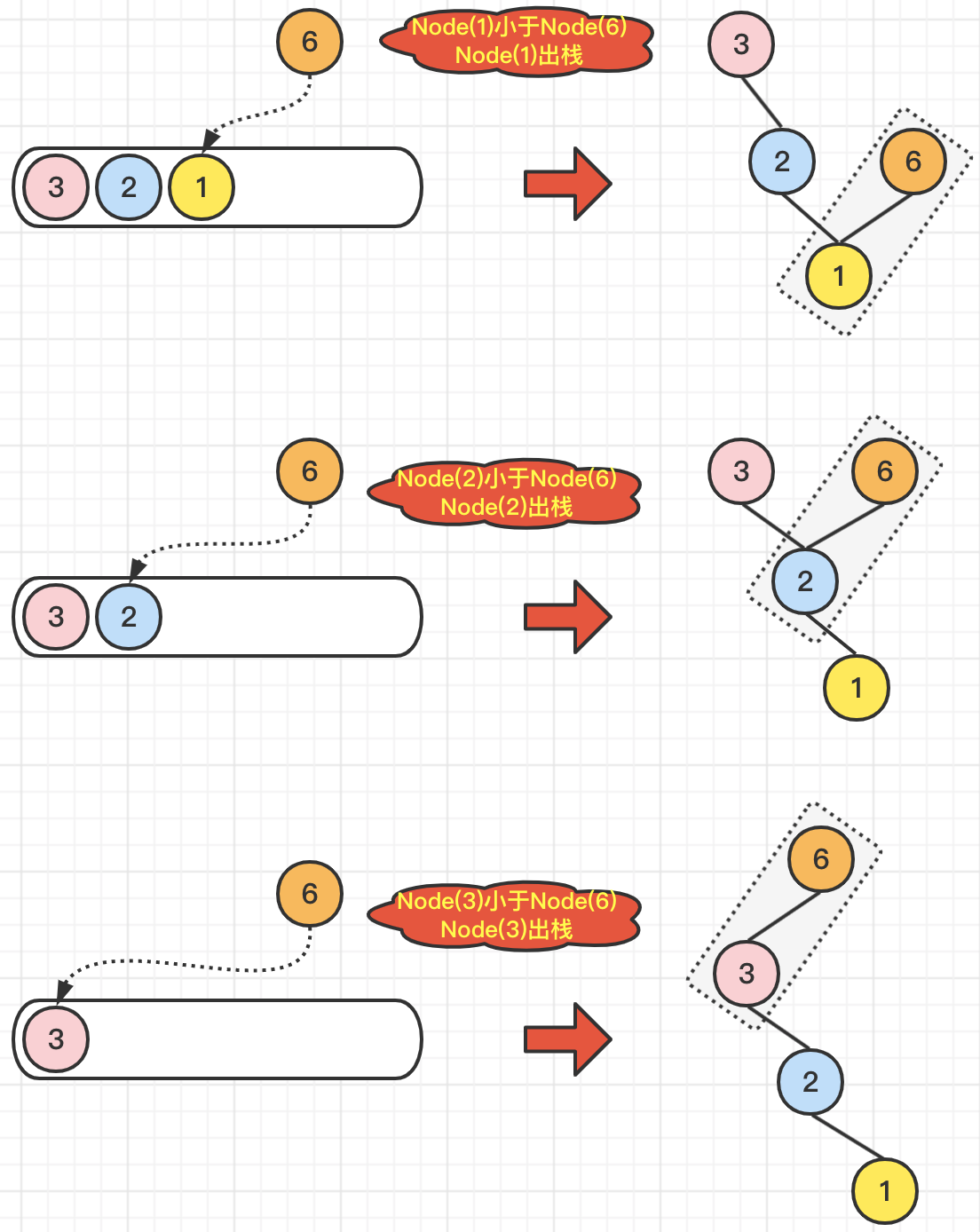

我们继续遍历到Node(0)，由于Node(0)小于栈顶元素Node(6)，所以Node(0)直接入栈就可以了。但是，别忘记维护一下二叉树，也就是说，配置一下Node(6).right = Node(0)。具体操作，如下图所示：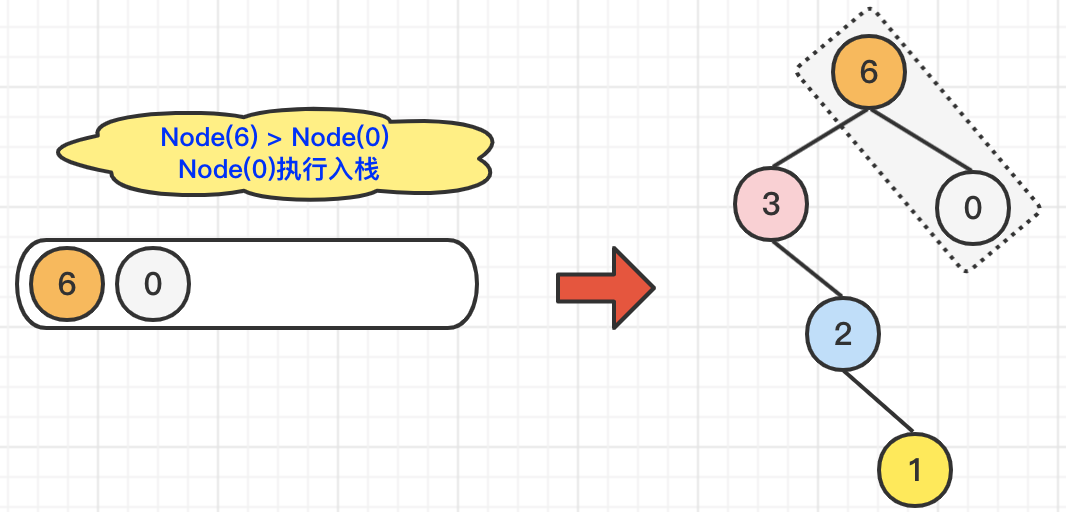

最后，我们遍历到了Node(5)，由于Node(5)大于当前栈顶元素Node(0)，所以Node(0)执行出栈操作，并维护二叉树结构Node(5).left = Node(0);在对比Node(5)小于当前栈顶元素Node(6)，所以，Node(5)直接入栈即可。维护二叉树结构Node(6).right = Node(5)。具体操作，如下图所示：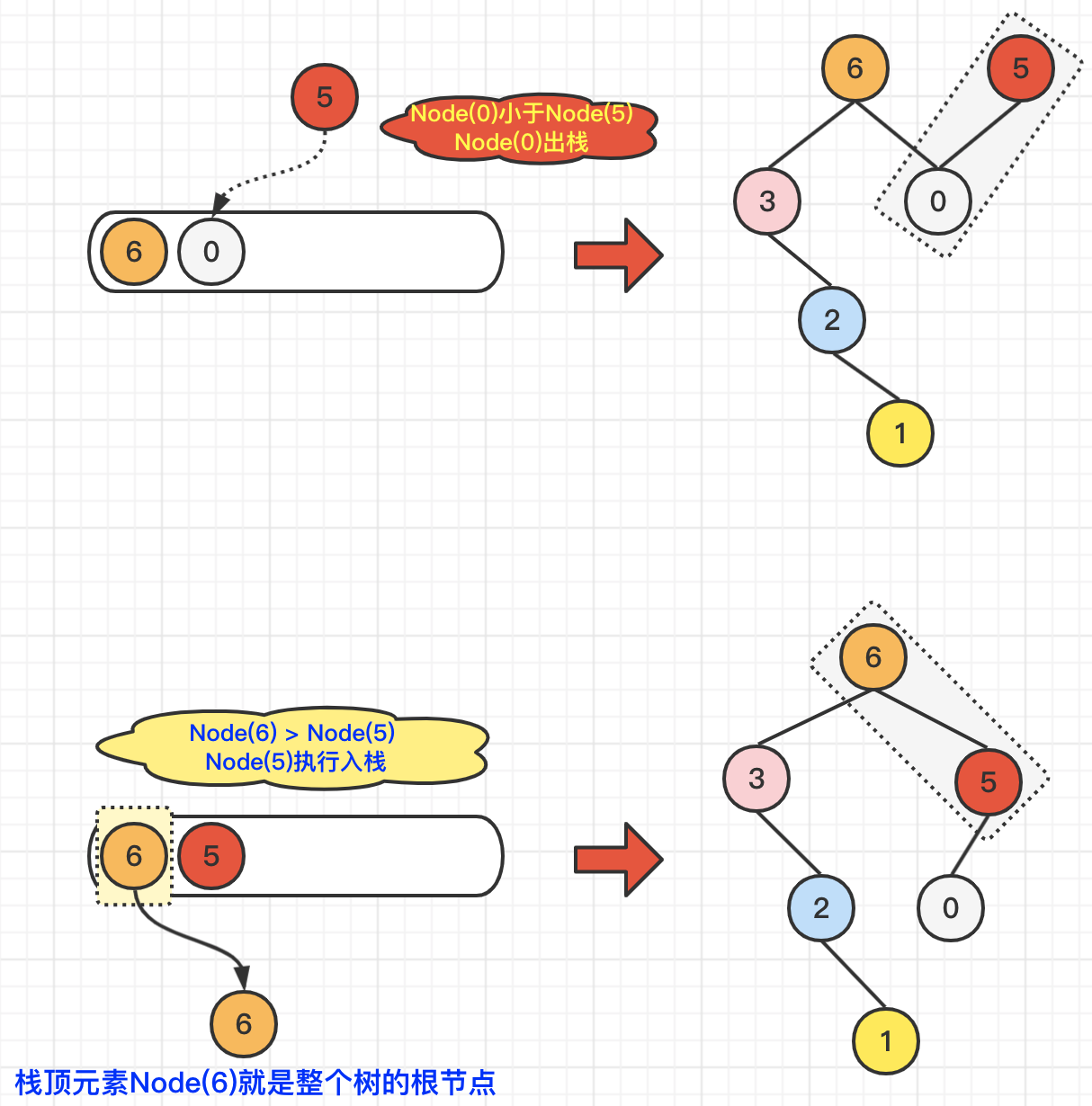

对于单调栈具体实现，逻辑上会没有思路1那么直观，特点其实就在于仅需对数组进行一次遍历，就可以构造好题目中所要求的二叉树结构。具体代码实现请参照 4.2> 实现2：单调栈

四、代码实现

4.1> 实现1：递归

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }
 
    public TreeNode build(int[] nums, int startIndex, int endIndex) {
        if (startIndex > endIndex) return null;
        int index = maxElementIndex(nums, startIndex, endIndex);
        TreeNode newNode = new TreeNode(nums[index]);
        newNode.left = build(nums, startIndex, index - 1);
        newNode.right = build(nums, index + 1, endIndex);
        return newNode;
    }
 
    public int maxElementIndex(int[] nums, int startIndex, int endIndex) {
        int maxIndex = startIndex;
        for (int i = startIndex + 1; i <= endIndex; i++) {
            maxIndex = nums[maxIndex] < nums[i] ? i : maxIndex;
        }
        return maxIndex;
    }
}

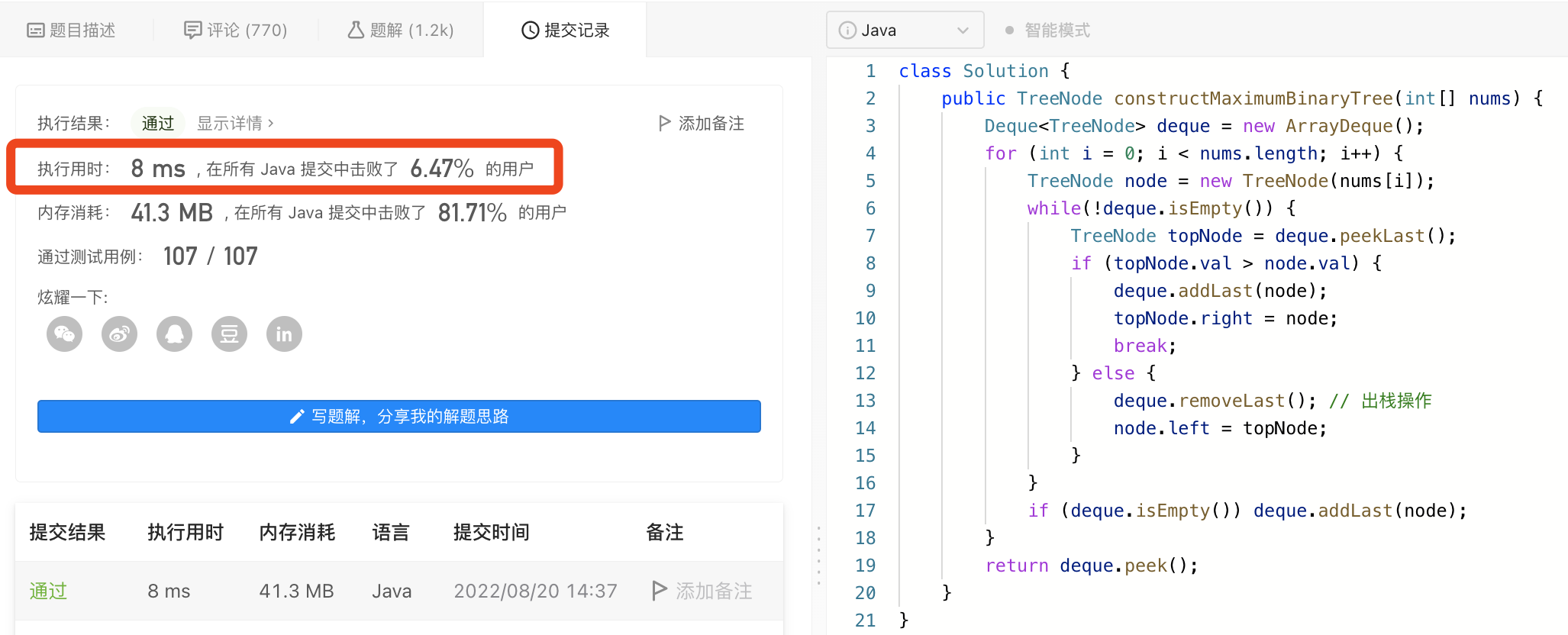
4.2> 实现2：单调栈

采用ArrayDeque实现堆栈结构

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        Deque<TreeNode> deque = new ArrayDeque();
        for (int i = 0; i < nums.length; i++) {
            TreeNode node = new TreeNode(nums[i]);
            while(!deque.isEmpty()) {
                TreeNode topNode = deque.peekLast();
                if (topNode.val > node.val) {
                    deque.addLast(node);
                    topNode.right = node;
                    break;
                } else {
                    deque.removeLast(); // 出栈操作
                    node.left = topNode;
                }
            }
            if (deque.isEmpty()) deque.addLast(node);
        }
        return deque.peek();
    }
}

采用数组实现堆栈结构

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        TreeNode[] deque = new TreeNode[1001];
        int tail = 0;
        for (int i = 0; i < nums.length; i++) {
            TreeNode node = new TreeNode(nums[i]);
            while(tail != 0) {
                TreeNode topNode = deque[tail - 1];
                if (topNode.val > node.val) {
                    deque[tail++] = node;
                    topNode.right = node;
                    break;
                } else {
                    deque[--tail] = null; // 出栈操作
                    node.left = topNode;
                }
            }
            if (tail == 0) deque[tail++] = node;
        }
        return deque[0];
    }
}

今天的文章内容就这些了：

写作不易，笔者几个小时甚至数天完成的一篇文章，只愿换来您几秒钟的 点赞 & 分享 。

更多技术干货，欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享，每天更新」