1339. 分裂二叉树的最大乘积-深度优先遍历

1339. 分裂二叉树的最大乘积

给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

示例 1：

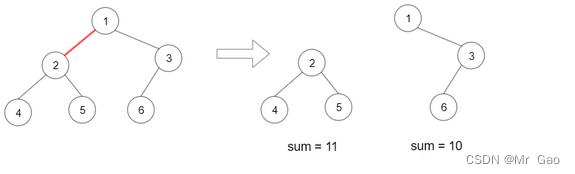
输入：root = [1,2,3,4,5,6]
输出：110
解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：

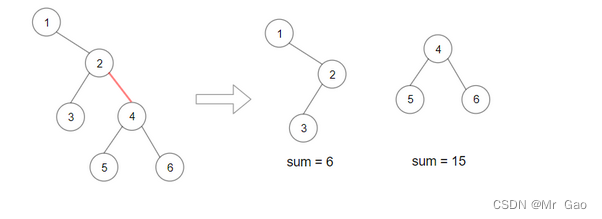
输入：root = [1,null,2,3,4,null,null,5,6]
输出：90
解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：

输入：root = [2,3,9,10,7,8,6,5,4,11,1]
输出：1025

示例 4：

输入：root = [1,1]
输出：1

这题还是很有趣的，建议先求出树的总体和，然后遍历每个子树，再计算最大值就可以了，很不错的题目

解题代码如所示：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

int sum_root(struct TreeNode* root){
    if(root){
        int a=sum_root(root->left);
        int b=sum_root(root->right);
        return a+b+root->val;

    }
    else{
        return 0;
    }
}

long long max;

long long find_max(struct TreeNode* root,int sum){
    if(root){
        long long a=find_max(root->left,sum);
        long long b=find_max(root->right,sum);
        long long maxt1=(sum-a)*a;
        long long maxt2=(sum-b)*b;
        max=fmax(max,fmax(maxt1,maxt2));
        return a+b+root->val;

    }
    else{
        return 0;
    }
}
int maxProduct(struct TreeNode* root){
    int sum=sum_root(root);
    printf(" sum %d ",sum);
    max=0;
    long long s=find_max(root,sum);

    return max%1000000007;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46