MATLAB神经网络编程（六）——BP神经网络的训练函数

《MATLAB神经网络编程》 化学工业出版社 读书笔记
第四章 前向型神经网络 4.3 BP传播网络

本文是《MATLAB神经网络编程》书籍的阅读笔记，其中涉及的源码、公式、原理都来自此书，若有不理解之处请参阅原书

---

1，BP网络的创建函数。
（1）newcf 函数 功能：用来创建级联前向BP网络，调用格式：

net=newcf(P,T,[S1,S2……S(N-1)]{TF1,TF2…TFN},BTF,BLF,PF,IPF,OPF,DDF)

P,T为每组输入元素的最大值和最小值组成的R*2维矩阵；Si为第i层的长度，共计NI层；TFi为第i层的传递函数，默认为”tansig”;BTF为BP网络的训练函数，默认为”trainlm”;BLF为权值和阈值的BP学习算法，默认为”learngdm”;PF为网络的性能函数，默认为”mse”；IPF为行输入的处理单元矩阵，默认为”fixunknowns”、“removeconstantrows”、“mapinmax”;OPF为行输出的处理单元矩阵，默认为“removeconstantrows”或“mapminmax”DDF为函数的定义默认为”dividerand”。

参数TFi可以采用任意的可微传递函数，如tansig,logsig,purelin等；训练函数可以是任意的BP训练函数，如trainlm,trainbfg,trainrp和traingd等。注意BTF默认采用trainlm是因为该函数的速度很快，但是该函数的缺点是运行会消耗大量的内存；如果内存不足建议采用trainfg或者trainrp,虽然这两个函数速度慢，但是占用内存小。

（2）newff 函数 功能：用来创建BP网络，调用格式：

net=newff(P,T,[S1 S2……S(N-1)],{TF1,TF2…TFN},BTF,BLF,PF,IPF,OPF,DDF)

参数含义同上。

（3）newfftd 函数 功能：用来创建一个存在输入延迟的前向型网络，调用格式：

net=newfftd(P,T,ID,[S1 S2……S(N-1)],{TF1,TF2…TFN},BTF,BLF,PF,IPF,OPF,DDF)

参数含义同上。

2,神经元上的传递函数

传递函数是BP网络的重要组成部分；又称激活函数，必须是连续可微的；BP网络常常采用S型对数或者正切函数或线性函数。

（1）logsig 函数 功能：S型的对数函数，调用格式：

A=logsig(N,FP)
info=logsig(code)

N为Q个S维的输入列向量；FP为功能结构参数；A为函数返回值，位于区间（0,1）中。
函数公式：

logsig(n) = 1 / (1 + exp(-n))

函数例子：

         n = -5:0.1:5;
        a = logsig(n);
        plot(n,a)
1
2
3

结果：

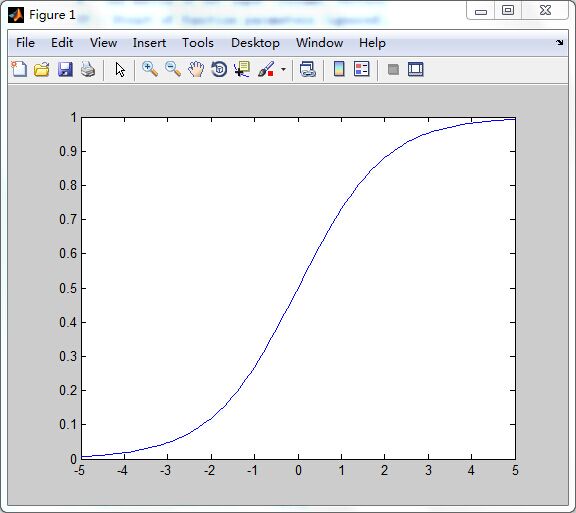
logsig函数可以将神经元的输入（范围是整个实数集）映射到区间（0,1）中。从形状上可以知道为何被称为S型函数。
使用语法：

net.layers{i}.transferFcn = ‘logsig’;

（2）tansig 函数 功能：双曲正切S型传递函数，调用格式：

A=tansig(N,FP)
info=logsig(code)

N为Q个S维的输入列向量；FP为功能结构参数；A为函数返回值，位于区间（-1,1）中(这也是与logsig函数不同的地方)。
函数公式：

a = tansig(n) = 2/(1+exp(-2*n))-1

函数例子：

        n = -5:0.1:5;
      a = tansig(n);
      plot(n,a)
1
2
3

结果：

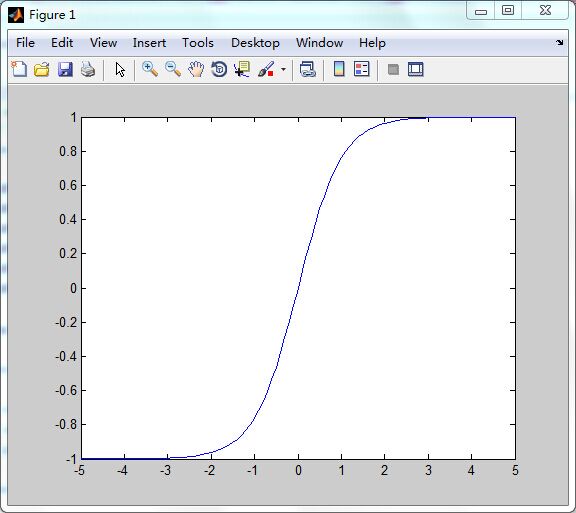
logsig函数可以将神经元的输入（范围是整个实数集）映射到区间（-1,1）中。从形状上可以知道为何被称为S型函数。
使用语法：

net.layers{i}.transferFcn = ‘tansig’;

（3）purelin 函数 功能：线性传递函数，调用格式：

A = purelin(N,FP)
dA_dN = purelin(‘dn’,N,A,FP)
INFO = purelin(CODE)

含义与上述相同，不同在于其输出等于输入，即A=N。

图像：

3，BP网络学习函数

（1） learngd函数 功能：梯度下降权值/阈值学习函数，通过神经元的输入和误差，以及权值和阈值的学习速率，来计算权值或者阈值的变化率。调用格式：

[dW,LS]=learngd(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
[db,LS]=learngd(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
info=learngd(code)

W为S*R维的权值矩阵；b为S维的阈值向量；P为Q组R维的输入向量；ones(1,Q)产生一个Q维的输入向量；Z为Q组S维的加权输入向量；N为Q组S维的输入向量；A为Q组S维的输出向量；T为Q组S维的层目标向量；E为Q组S维的层误差向量；gW为与性能相关的S*R维梯度；gA为与性能相关的S*R维输出梯度；D为S*S的神经元距离矩阵；LP为学习参数，可通过该参数设置学习速率，格式：LP.lr=0.01;LS为学习状态初始为空；dW为S*R维的权值或阈值变化率矩阵；db为S 维的阈值变化率向量；LS为新的学习状态。

info=learngd(code)：根据不同的code值返回有关函数的不同信息，包括：

• pnames——返回设置的学习参数；
• pdefaults——返回默认的学习参数；
• needg——如果函数使用了gW或者gA，则返回1；

（2） learngdm函数 功能：梯度下降动量学习函数，利用神经元的输入和误差、权值和阈值的学习速率和动量常数，来计算权值或阈值的变化率。调用格式：

[dW,LS]=learngdm(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
[db,LS]=learngdm(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
info=learngdm(code)

含义参考learngd函数。

动量常数mc是通过学习参数LP设置的，格式为”LP.mc=0.8”

4，BP网络训练函数。
（1）trainbfg函数 功能：该函数为BFGS准牛顿BP算法函数。除了BP网络外，该函数也可以训练任意形式的神经网络，只要它的传递函数对于权值和输入存在导函数即可。调用格式：

[net,TR]=trainbfg(NET,Pd,trainV,valV,testV)
info=trainbfg(‘info’)

NET是待训练的神经网络；Pd是有延迟的输入向量；trainV是训练向量结构或者为空；valV是确认向量结构或者空；testV是检验向量结构或者空。net是训练之后的神经网络；TR是每一步训练的有关信息记录，包括：

• pnames——返回设定的训练参数；
• pdefaults——返回默认的训练参数；

在利用该函数进行BP网络训练时候，MATLAB已经默认了以下训练参数：

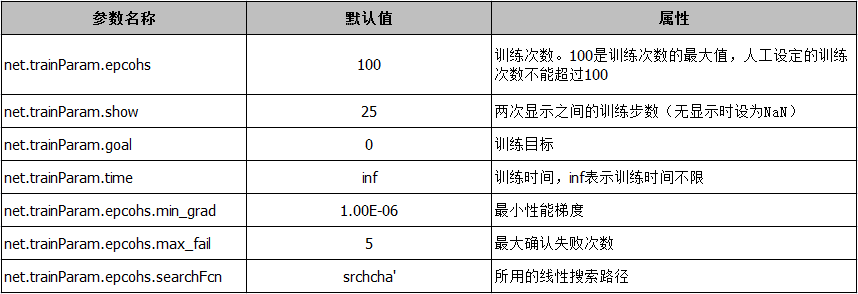
【实例】

clear all;
P = [0 1 2 3 4 5];
T = [0 0 0 1 1 1];
net = newff(P,T,2,{},'trainbfg');
a1 = sim(net,P)
net = train(net,P,T);
a 2= sim(net,P)
1
2
3
4
5
6
7

输出：

a1 =

    0.5644    0.7726    0.8168    0.8255    0.8565    1.0009


a2 =

   -0.1019   -0.0030    0.0405    0.2829    0.9420    1.0963
1
2
3
4
5
6
7
8

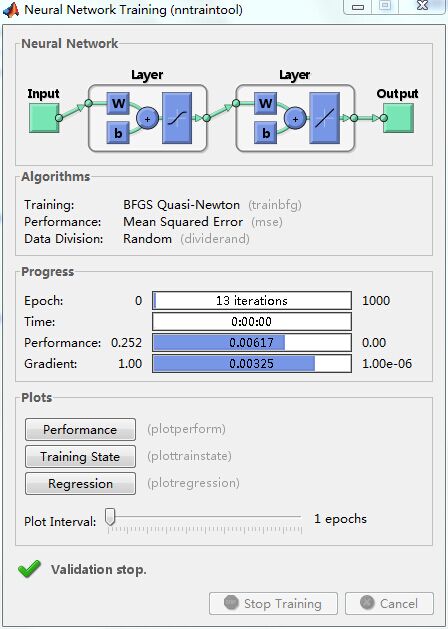
（2） traingd函数 功能：该函数为梯度下降BP算法函数。调用格式：

[net,TR]=traingd(NET,TR,trainV,valV,testV)
info=traingd(‘info’)

参数含义、函数用法与trainbfg相同

5，性能函数
（1） mse函数 功能：均方误差性能函数。调用格式：

perf=mse(E,Y,X,FP)
info=mse(code)

含义与mae函数相同。

（1） msereg函数 功能：也是性能函数，通过两个因子的加权和来评价网络的性能，分别是均方误差、均方权值和阈值。调用格式：

perf=msereg(E,Y,X,FP)
info=mse(code)

含义与mae函数相同。

在使用该函数之前，需要设定性能参数FP，格式：FP.ratio=0.3;含义是误差相对于权值和阈值的重要性。函数返回值=均方误差*FP.ratio+均方权值和阈值*FP.ratio

【例子】

clear all;
% 创建一个BP网络
net=newff([-2 2],[4 1],{'tansig','purelin'},'trainlm','learngdm','msereg');
p=[-2 -1 0 1 2];
t=[0 1 1 1 0];
y=sim(net,p)
e=t-y          %误差向量
net.performParam.ratio=20/(20+1);  %设置性能参数
perf=msereg(e,net)
1
2
3
4
5
6
7
8
9

输出：

y =

    1.2278    0.8577   -0.7544   -2.3127   -2.1899


e =

   -1.2278    0.1423    1.7544    3.3127    2.1899

perf =

    3.6676
1
2
3
4
5
6
7
8
9
10
11
12

6，显示函数
（1）plotperf函数 功能：该函数用来绘制网络的性能。调用格式：

plotperf(tr,goal,name,epoch)

tr是网络的训练记录；goal是性能目标，默认是NaN；name是训练函数的名称，默认为空；epoch是训练步数，默认是训练记录的长度。
函数除了可以绘制网络的训练性能外，还可以绘制性能目标、确认性能和检验性能，前提是他们都存在。

（2）plotes函数 功能：用来绘制一个单独神经元的误差曲面。调用格式：

plotes(WV,BV,ES,V)

WV是权值的N维行向量；BV是M维的阈值行向量；ES是误差向量组成的M*N维矩阵。V是视角默认是[-37.5,30]。
函数绘制的误差曲面图是有权值和阈值确定、由函数errsurf计算得出的。

（3）plotep函数 功能：用来绘制权值和阈值在误差曲面上的位置。调用格式：

h=plotep(W,B,E)
h=plotep(W,B,E,H)

W是当前权值；B是当前阈值；E是当前单输入神经元的误差；H是权值和阈值在上一时刻的位置信息向量；h是当前的权值和阈值位置信息向量。

(4) errsurf函数 功能：用来计算单个神经元的误差曲面。调用格式：

errsurf(P,T,WV,BV,F)

P是输入行向量；T是目标行向量；ＷＶ是权值列向量；ＢＶ是阈值列向量；Ｆ是传递函数的名称。
【例４－３３】分析一个ＢＰ网络中某个神经元的误差，并绘制出其误差曲面与轮廓线。

 clear all;
P = 1:8; T = sin(P);
net = newff(P,T,4); 
[net,tr] = train(net,P,T);
p = [3 2];
t = [0.4 0.8];
wv = -4:0.4:4; bv = wv;
ES = errsurf(p,t,wv,bv,'logsig');
plotes(wv,bv,ES,[60 30])
1
2
3
4
5
6
7
8
9

运行结果：

---