学习笔记：机器学习之支持向量机(五、线性支持向量机-合页损失函数)

活动地址：CSDN21天学习挑战赛

​1 合页损失函数

  前一节是通过解决凸二次规划问题获得分类超平面，线性支持向量机还有另一种解释方式，最小化以下目标函数：
$$\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda ||w|{|}^2$$
$L(y(w\cdot x+b))=[1-y(w\cdot x+b){]}_{+}$称为合页损失函数(hinge loss function)
[ z ] + = { z , z > 0 0 , z ⩽ 0 [z]_{+}=\left\{

\right. [z]+​={z,0,​z>0z⩽0​，"+"表示取正值，其他取值为0。
用合页损失函数对原来的目标函数进行变换：
$$\underset{w,b}{\min }C\sum _{i=1}^N{\left[1-y_i\left(w\cdot x_i+b\right)\right]}_{+}+\frac{\Vert w{\Vert }^2}{2}$$
令$\frac{1}{2C}=\lambda$,则：
$$\underset{w,b}{\min }\sum _{i=1}^N{\left[1-y_i\left(w\cdot x_i+b\right)\right]}_{+}+\lambda \Vert w{\Vert }^2$$

2 三个损失函数的比较

  0-1损失函数、感知机损失函数、合页损失函数的比较。

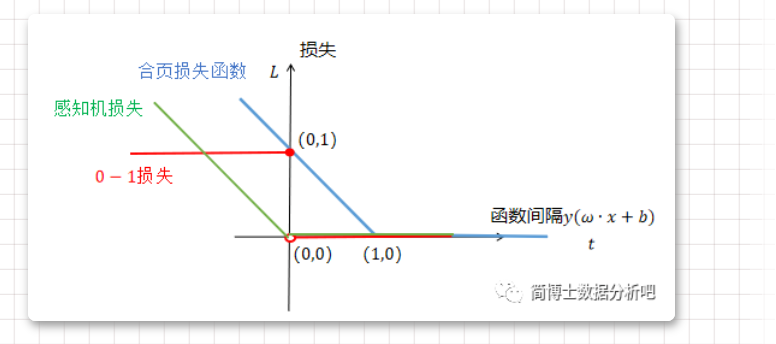
  对于合页损失函数来说，只有函数间隔小于1时，损失值为1-t，由此可见SVM不仅要求分类正确还要确信度尽可能高。

参考

1.《统计学习方法》——李航
2. https://mp.weixin.qq.com/s/mbjigfoc-SXJ6QsR0tc96A