2022_08_08__106期__二叉树_堆

目录

堆排序：

堆排序：

topK问题：

打印文件里前K大的元素：

随机数打印：

---

堆排序：

方法：建堆，向上调整建堆

void HeapSort(int *a, int n)
{
	for (int i = 1; i < n; ++i)
	{
		AdjustUp(a, i);
	}
}
int main()
{
	int a[] = { 65, 100, 70, 32, 50, 60 };
	HeapSort(a, sizeof(a) / sizeof(int));
	return 0;
}

数组a有几个元素，我们调用堆排序函数，传递的参数是数组首元素的地址和数组的元素个数。

我们在函数内部调用for循环，循环n次，调用向上调整函数。

把我们的数组元素以栈的形式重新输入。

我们也可以用向下调整的方法：

我们先求最后一个节点的父亲

 最后一个节点是70，最后一个节点对应的父亲是60，假如我们要求的是大根堆：

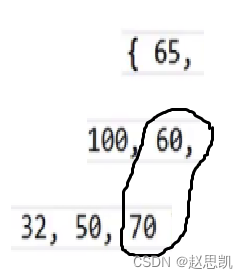
 先让60和70进行比较，60<70，所以我们要进行交换：

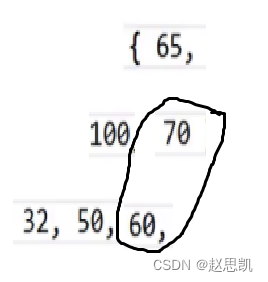
 然后70对应的下标--，找到100，求出100的两个孩子，让100与两个孩子进行比较，因为100这个堆是大根堆，所以不需要调整：

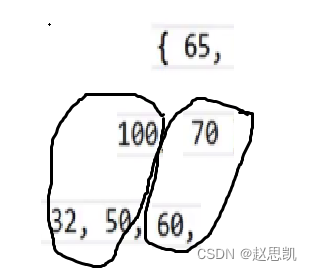
 然后100对应的下标-1，指向堆头。然后我们再进行向下调整

我们再举一个例子：

 我们首先求最后一个节点对应的父亲，也就是8，我们让7和8进行比较。

 比较之后，我们进行交换，交换这里我们先不演示：

然后根据8对应的下标求25对应的下标，让25和两个孩子进行比较：

然后根据25对应的下标再求出19对应的下标，然后让19对对应的两个孩子节点进行比较：

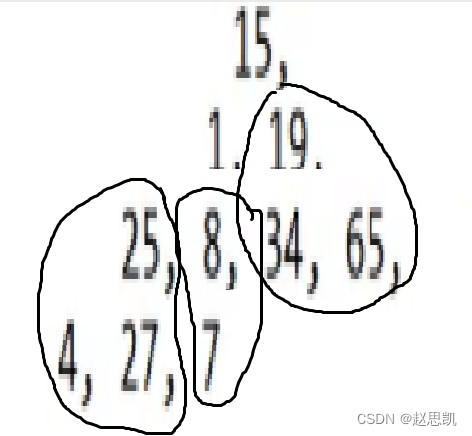
 同理：

 

 我们用代码的形式写一下：

void HeapSort(int *a, int n)
{
	for (int i = (n-1-1)/2; i >=0; --i)
	{
		AdjustDown(a, n, i);
	}
}

n-1表示最后一个元素对应的下标，再-1/2表示求出最后一个节点的父亲节点，然后调用向下调整函数。

向上调整建堆的时间复杂度为O(N*logn),原因是我们循环N次，2^m-1=N,求出m大概等于logN，m就是高度，我们每一个运算执行的次数就是m-1次，所以向上调整建堆的时间复杂度为O(N*logn).

接下来，我们计算向下调整建堆的时间复杂度：

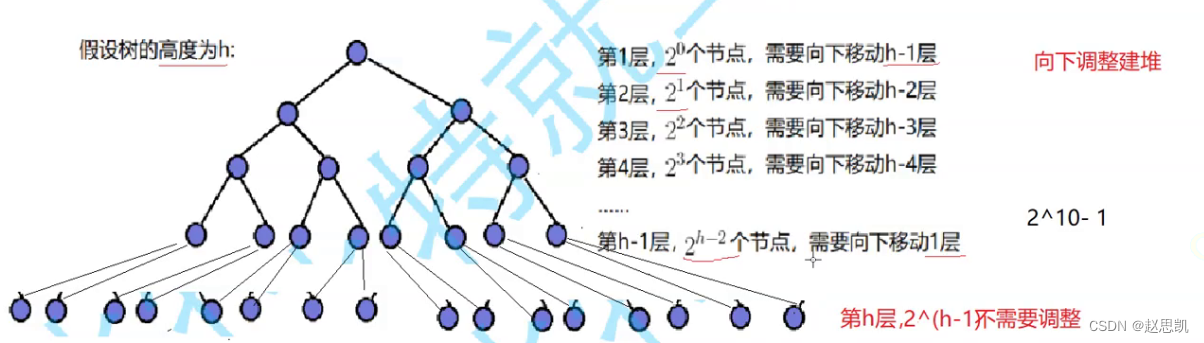
由图像可知，我们的第一层，有一个节点，我们的高度为h的话，第一层最坏要向下移动h-1次，

第二层，有2个节点，每一个节点最坏要向下移动h-2次，第h-1层，有2^h-2个节点，需要向下移动一层，而最后一层我们不需要移动。

所以一共要移动多少次呢？

 我们使用错位相减法：

 

 计算的结果为-h+2^h-1.

高度为h，节点数量为N时，2^h-1=N,所以h=logN，2^h等于N，所以计算的结果就为O(N)

所以向下调整的时间复杂度就是O(N)

所以我们建堆最好用向下调整，向下调整更快。

堆排序：

我们进行思考，假如我们要对大根堆进行排序，那我们应该是升序还是降序：

正常而言是降序的，因为大根堆的堆顶元素是最大的。

 许多人的想法是去掉堆顶元素，然后重新建堆排列，这种方法无论是时间复杂度还是复杂程度都不符合我们的要求，我们可以换一种写一种写法：

我们把堆顶和堆尾的元素进行交换：

 然后对其他元素进行向下调整，就能够找出次大的元素了。

我们写代码进行演示：

void HeapSort(int *a, int n)
{
	for (int i = (n-1-1)/2; i >=0; --i)
	{
		AdjustDown(a, n, i);
	}
	int i = 1;
	while (i < n)
	{
		Swap(&a[0], &a[n-i]);
		AdjustDown(a, n-i, 0);
		++i;
	}
}

 我们第一个for循环表示把我们的数组转化为小根堆或者大根堆

创建变量i为1，执行while循环，n表示数组的元素个数，当i加到与n相等的时候，我们退出循环，我们在循环中首先要交换首位的元素，然后我们把除尾部元素其他元素重新向下排列，这时候堆顶的元素就是次大的元素。

我们持续调用函数：这时候就能把大根堆重新排列成从大到小。

所以，假如我们要从小到大排列时，我们需要首先把数组转化为大根堆

我们要从大到小排列时，我们需要先把数组转化为小根堆。

假设我们的高度为M，2^M=N,所以M=logN，我们有N个元素，每个元素最多计算M-1次，所以时间复杂度为O(N*logN）

topK问题：

 假如我们求前K个最大的元素，我们正常的思路是用大堆，把大的元素放在下面，小的元素放在上面，我们的最后k个元素就是最大的k个元素，我们popK次即可，但是假如我们的N非常大，我们的N是十亿，假如我们使用大堆的方法，我们就需要创建十亿个整型的空间，空间浪费太过于严重。

这种方法的时间复杂度为O(N+KlogN).

假如我们用小堆的思路：

假如我们的N是十亿，我们的k只有20，我们可以采用小堆的方法：我们创建一个20的小堆，包含数组的前20个元素，我们依次遍历后N-k个元素，遇到大的就和堆顶的元素交换，然后向下调整进堆。

时间复杂度为O(K+(N-K)*logK)

打印文件里前K大的元素：

void PrintTopK(const char*filename, int k)
{
	assert(filename);
	FILE*fout = fopen(filename, "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}
	int*minHeap=(int*)malloc(sizeof(int)*k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}
	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	for (int j = (k - 2) / 2; j >= 0; --j)
	{
		AdjustDown(minHeap, k, j);
	}
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}
	for (int i = 0; i < k; ++i)
	{
		printf("%d", minHeap[i]);
	}
	free(minHeap);
	fclose(fout);
}
int main()
{
	const char*filename = "Data.txt";
	int k = 3;
	PrintTopK(filename, k);
}

我们对代码进行分析：

我们首先在电脑中创建一个文件，文件名为“Data.txt"，我们在文件中输入几个数字，创建变量k为3，k表示我们要打印文件中的前3大的元素。

PrintTopK(filename, k);

调用函数PrintTopK，函数的第一个参数是文件名，第二个参数是要打印的元素个数。

接下来，我们看函数的定义：

void PrintTopK(const char*filename, int k)
{
	assert(filename);
	FILE*fout = fopen(filename, "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

首先，我们对文件指针进行断言，防止其为空指针。

然后我们以读的形式打开文件，返回文件指针

如果文件指针为空指针，表示我们打开文件失败，我们打印对应的错误信息，然后退出函数。

int*minHeap=(int*)malloc(sizeof(int)*k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}

接下来，我们进行动态内存开辟空间，这部分空间是用来建堆的。

我们需要求前K个元素的大小，所以我们要开辟k个元素的数组，该数组用来存放K个元素。

如果malloc申请失败的话，打印对应的错误信息，然后退出函数。

for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}

这个循环是把文件中的前K个元素读取到数组的前K个空间中。

fscanf(fout, "%d", &minHeap[i]);

fout为文件指针，我们通过文件指针，读取到文件中的元素，以读取整型的方式，把文件中的元素读取到数组中去。

for (int j = (k - 2) / 2; j >= 0; --j)
	{
		AdjustDown(minHeap, k, j);
	}

这里我们先定义以下向下调整函数：

void AdjustDown(HPDataType*a, int n, int parent)
{
	int minchild = parent * 2 + 1;
	
	while (minchild < n)
	{
		if (minchild + 1 < n&&a[minchild + 1] < a[minchild])
		{
			minchild++;
		}
		if (a[minchild] < a[parent])
		{
			Swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}

向下调整函数一般是用来建堆的，第一个参数表示数组名，表示我们要在该数组中建堆，第二个参数代表我们的堆的元素个数，k-1表示最后一个元素对应的下标，k-1-1/2表示最后一个元素对应的父亲节点对应的下标。

int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}

创建参数val为0，执行循环，读取文件中的值，！=EOF的意思就是文件读取结束了。

逐步进行遍历，当val比堆的堆顶的元素大的时候，我们交换val与堆顶的元素。

然后再次向下调整，时堆从小到大排列，当遍历结束后，我们就找出了文件中前K大的元素。

for (int i = 0; i < k; ++i)
	{
		printf("%d", minHeap[i]);
	}
	free(minHeap);
	fclose(fout);

我们循环打印堆中的元素，打印的就是前K大的元素。

因为我们的堆的空间是动态内存申请的，所以我们使用free释放，防止造成内存泄漏，然后关闭文件。

随机数打印：

void CreateDataFile(filename, N)
{
	FILE*fin = fopen(filename, "w");
	if (fin == NULL)
	{
		perror("fopen fail");
		return;
	}
	srand(time(0));
	for (int i = 0; i < N; ++i)
	{
		fprintf(fin, "%d", rand());
	}
	fclose(fin);
}
 
void PrintTopK(const char*filename, int k)
{
	assert(filename);
	FILE*fout = fopen(filename, "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}
	int*minHeap = (int*)malloc(sizeof(int)*k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	for (int j = (k - 2) / 2; j >= 0; j--)
	{
		AdjustDown(minHeap, k, j);
	}
	int val = 0;
	while (scanf(fout, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}
	for (int i = 0; i < k; i++)
	{
		printf("%d ", minHeap[i]);
	}
	free(minHeap);
	fclose(fout);
}
int main()
{
	const char*filename = "Data.txt";
	int N = 10000;
	int k = 10;
	CreateDataFile(filename, N);
	PrintTopK(filename, k);
	return 0;
}

随机数函数：

void CreateDataFile(filename, N)
{
	FILE*fin = fopen(filename, "w");
	if (fin == NULL)
	{
		perror("fopen fail");
		return;
	}
	srand(time(0));
	for (int i = 0; i < N; ++i)
	{
		fprintf(fin, "%d", rand());
	}
	fclose(fin);
}

我们对代码进行分析：我们以写的形式打开文件filename，返回文件指针fin，进行判断，如果文件指针为空指针，证明打开文件失败，我们打印对应的错误信息，然后退出函数。

srand(time(0))相当与就是一个时间戳，当我们要使用随机数时，我们需要引入时间戳

我们调用for循环，在文件中以整形的形式写入随机数，然后关闭文件。