MATLAB | 如何绘制高斯混合分布分类区域及边界

在下面这篇中，我们已经说明了如何对数据进行高斯混合分布聚类并绘制概率密度曲面及置信椭圆：https://slandarer.blog.csdn.net/article/details/121521677

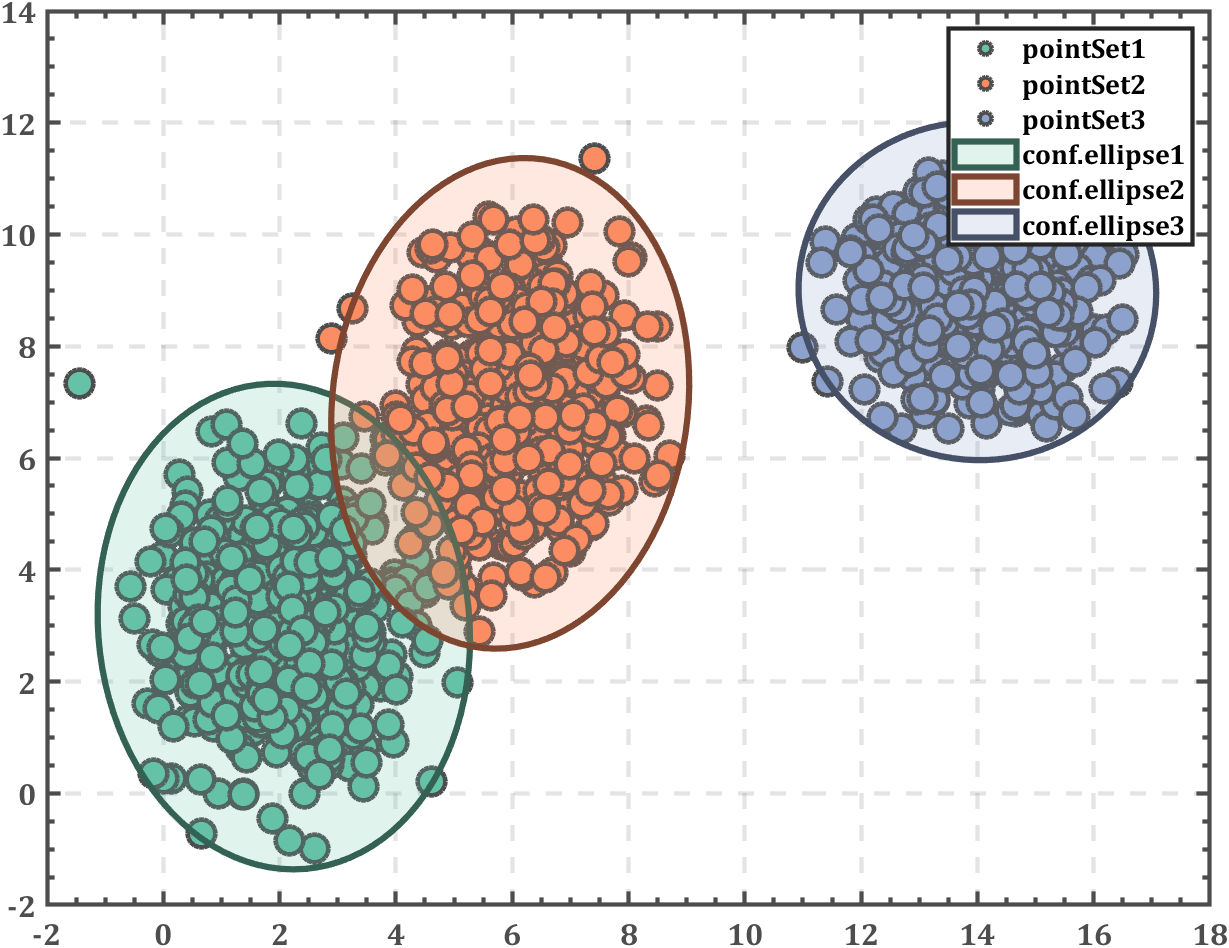
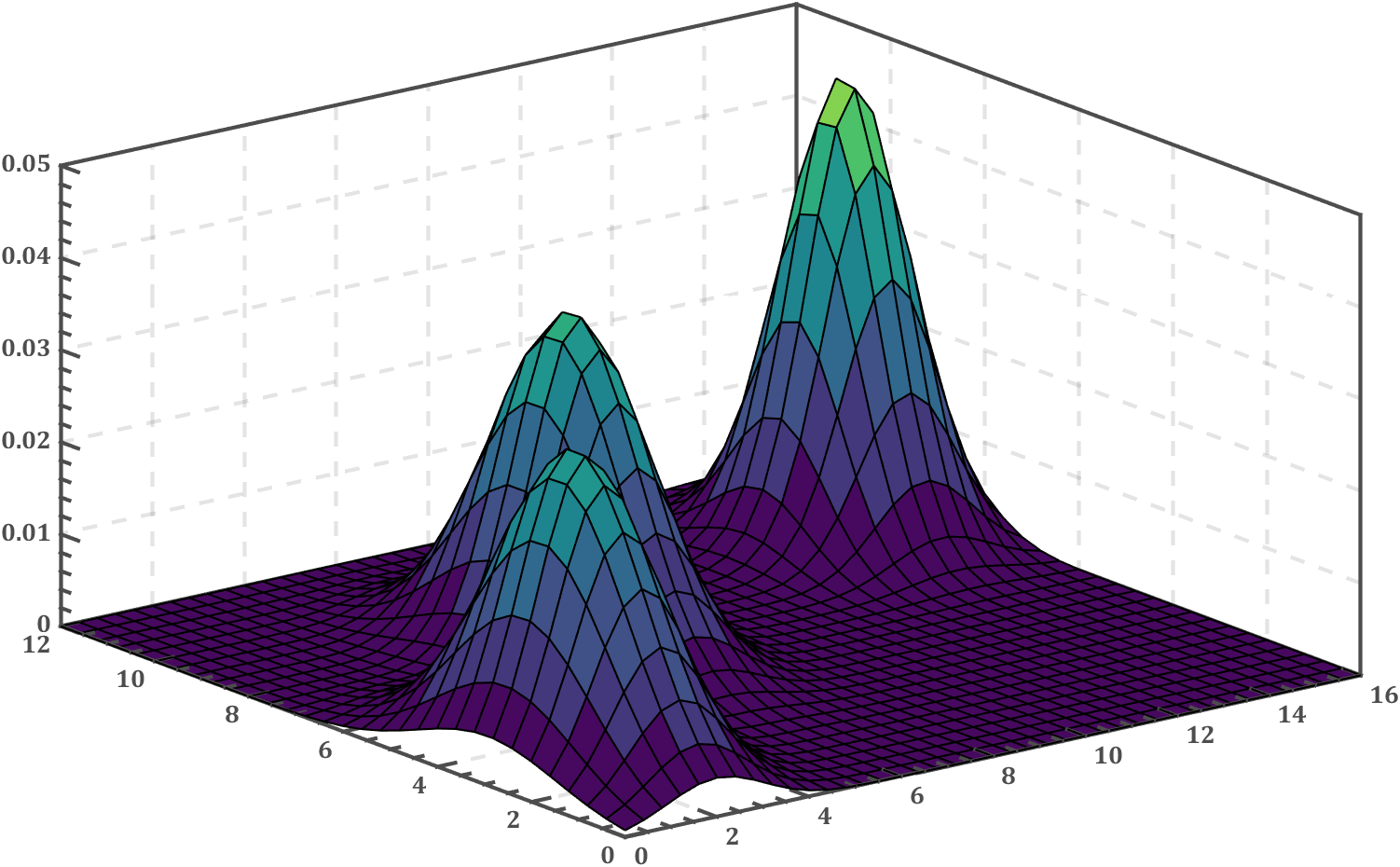
那么这篇要解决的问题就是如何绘制聚类区域与边界：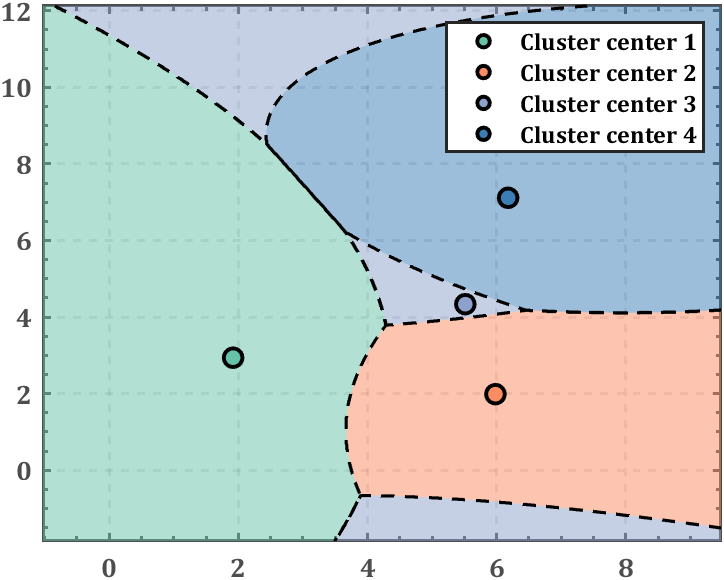

---

1 工具函数

首先先把工具函数都给出一遍，之后讲解如何绘制绘制聚类区域与边界：

1.1 高斯混合模型聚类

function [Mu,Sigma,Pi,Class]=gaussKMeans(pntSet,K,initM)
% @author:slandarer
% ===============================================================
% pntSet  | NxD数组   | 点坐标集                                |
% K       | 数值      | 划分堆数量                              |
% --------+-----------+-----------------------------------------+
% Mu      | KxD数组   | 每一行为一类的坐标中心                  |
% Sigma   | DxDxK数组 | 每一层为一类的协方差矩阵                |
% Pi      | Kx1列向量 | 每一个数值为一类的权重(占比)            |
% Class   | Nx1列向量 | 每一个数值为每一个元素的标签(属于哪一类)|
% --------+-----------+-----------------------------------------+


[N,D]=size(pntSet); % N:元素个数 | D:维数

% 初始化数据===============================================================
if nargin<3
    initM='random';
end
switch initM
    case 'random' % 随机取初始值
        [~,tIndex]=sort(rand(N,1));tIndex=tIndex(1:K);
        Mu=pntSet(tIndex,:);

    case 'dis'    % 依据各维度的最大最小值构建方向向量
                  % 并依据该方向向量均匀取点作为初始中心       
        tMin=min(pntSet);
        tMax=max(pntSet);
        Mu=linspace(0,1,K)'*(tMax-tMin)+repmat(tMin,K,1);

    % case '依据个人需求自行添加'  
    % ... ...
    % ... ...     
end

% 一开始设置每一类有相同协方差矩阵和权重
Sigma(:,:,1:K)=repmat(cov(pntSet),[1,1,K]);
Pi(1:K,1)=(1/K);

% latest coefficient:上一轮的参数
LMu=Mu;        
LPi=Pi;
LSigma=Sigma;

turn=0; %轮次

% GMM/gauss_k_means主要部分================================================
while true
    
    % 计算所有点作为第k类成员时概率及概率和(不加权重)
    % 此处用了多次转置避免构建NxN大小中间变量矩阵
    % 而将过程中构建的最大矩阵缩小至NxD，显著减少内存消耗
    Psi=zeros(N,K);
    for k=1:K
        Y=pntSet-repmat(Mu(k,:),N,1);
        Psi(:,k)=((2*pi)^(-D/2))*(det(Sigma(:,:,k))^(-1/2))*...
                      exp(-1/2*sum((Y/Sigma(:,:,k)).*Y,2))';    
    end
    
    % 加入权重计算各点属于各类后验概率
    Gamma=Psi.*Pi'./sum(Psi.*Pi',2);
    
    % 大量使用矩阵运算代替循环，提高运行效率
    Mu=Gamma'*pntSet./sum(Gamma,1)';
    for k=1:K
        Y=pntSet-repmat(Mu(k,:),N,1);
        Sigma(:,:,k)=(Y'*(Gamma(:,k).*Y))./sum(Gamma(:,k));
    end
    Pi=(sum(Gamma)/N)';
    [~,Class]=max(Gamma,[],2);

    % 计算均方根误差
    R_Mu=sum((LMu-Mu).^2,'all');
    R_Sigma=sum((LSigma-Sigma).^2,'all');
    R_Pi=sum((LPi-Pi).^2,'all');
    R=sqrt((R_Mu+R_Sigma+R_Pi)/(K*D+D*D*K+K));
    
    % 每隔10轮输出当前收敛情况
    turn=turn+1;
    if mod(turn,10)==0
        disp(' ')
        disp('==================================')
        disp(['第',num2str(turn),'次EM算法参数估计完成'])
        disp('----------------------------------')
        disp(['均方根误差:',num2str(R)])
        disp('当前各类中心点：')
        disp(Mu)
    end
    
    % 循环跳出
    if (R<1e-6)||isnan(R)
        disp(['第',num2str(turn),'次EM算法参数估计完成'])
        if turn>=1e4||isnan(R)
            disp('GMM模型不收敛')
        else
            disp(['GMM模型收敛，参数均方根误差为',num2str(R)])
        end
        break;
    end   
    LMu=Mu;
    LSigma=Sigma;
    LPi=Pi;
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

1.2 概率密度函数获取

就是一个比较复杂的函数获取(公式显示不全可左右滑动)：

首先是高斯分布的函数：

$$\mathcal{N}(\mathbf{x}\mid \mathbf{\mu },\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\mathbf{\Sigma }{|}^{1/2}}\exp \left[-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })\right]$$

那么高斯混合分布的函数就是好几个上面的高斯分布函数乘以系数再相加：
$$p(\mathbf{x})=\sum _{k=1}^K{\pi }_k\mathcal{N}\left(\mathbf{x}\mid {\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k\right)$$

function func=getGaussFunc(Mu,Sigma,Pi)
[K,D]=size(Mu);

X{D}=[];
for d=1:D
    X{d}=['x',num2str(d)];
end
X=sym(X);

func=0;
for k=1:K
    tMu=Mu(k,:);
    tSigma=Sigma(:,:,k);   
    tPi=Pi(k);
    tX=X-tMu;   
    func=func+tPi*(1/(2*pi)^(D/2))*(1/det(tSigma)^(1/2))*exp((-1/2)*(tX/tSigma*tX.'));
end

func=matlabFunction(func);
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

1.3 置信椭圆获取

function [X,Y]=getEllipse(Mu,Sigma,S,pntNum)
% 置信区间 | 95%:5.991  99%:9.21  90%:4.605
% (X-Mu)*inv(Sigma)*(X-Mu)=S

invSig=inv(Sigma);

[V,D]=eig(invSig);
aa=sqrt(S/D(1));
bb=sqrt(S/D(4));

t=linspace(0,2*pi,pntNum);
XY=V*[aa*cos(t);bb*sin(t)];
X=(XY(1,:)+Mu(1))';
Y=(XY(2,:)+Mu(2))';
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

---

2 聚类区域及边界绘制

2.1 数据及混合模型

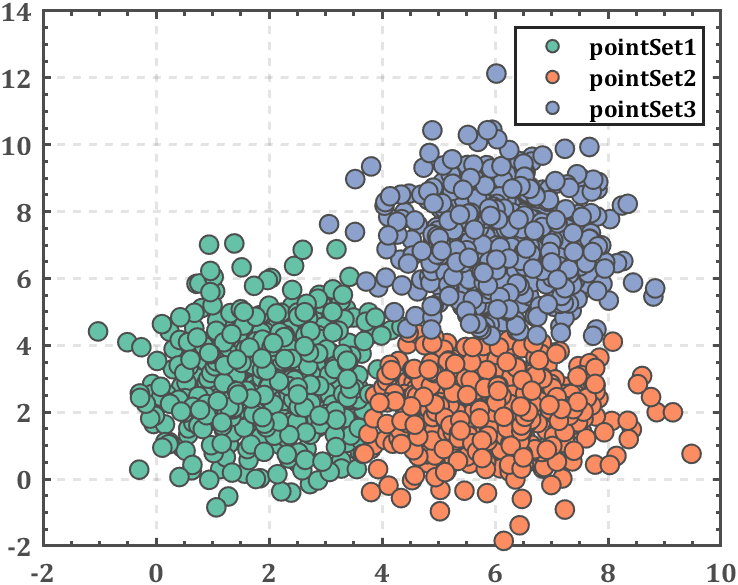
以下是随机生成的一组数据，对其进行一次高斯混合分布聚类：

% 构造三个符合高斯分布的点集并合并
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([6 2],[1 0;0 1],500);
X=[PntSet1;PntSet2;PntSet3];

% 分类数量
K=3;

% 构造GMM模型
tic
[Mu,Sigma,Pi,Class]=gaussKMeans(X,K,'dis');
toc
1
2
3
4
5
6
7
8
9
10
11
12
13

看一下分类结果：

% 配色
colorList=[0.4  0.76 0.65
           0.99 0.55 0.38 
           0.55 0.63 0.80
           0.23 0.49 0.71
           0.95 0.57 0.47
           0.94 0.65 0.12
           0.70 0.26 0.42
           0.86 0.82 0.11];
% -------------------------------------------------------------------------
% 绘制聚类情况
figure()
hold on
strSet{K}='';
for i=1:K
    scatter(X(Class==i,1),X(Class==i,2),80,'filled',...
        'LineWidth',1,'MarkerEdgeColor',[1 1 1]*.3,'MarkerFaceColor',colorList(i,:));
    strSet{i}=['pointSet',num2str(i)];
end
legend(gca,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=13;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

2.2 聚类区域绘制

这里提供俩方法哈，不过不过不管咋样两个方法的思路都是先把坐标区域细分成网格，计算每个格点属于哪个类：

细分网格并计算格点归属

% 构造细密网格
x1=min(X(:,1)):0.01:max(X(:,1));
x2=min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G]=meshgrid(x1,x2);
XGrid=[x1G(:),x2G(:)];

% 检测每个格点属于哪一类
XV=zeros(size(XGrid,1),K);
for i=1:K
    tf=getGaussFunc(Mu(i,:),Sigma(:,:,i),Pi(i));
    XV(:,i)=tf(x1G(:),x2G(:));
end 
[~,idx2Region]=max(XV,[],2);
1
2
3
4
5
6
7
8
9
10
11
12
13

方法一：
假如安装了Statistics and Machine Learning Toolbox工具箱可以直接用gscatter函数：

% 绘制聚类区域方法一
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,colorList,'..');
1
2

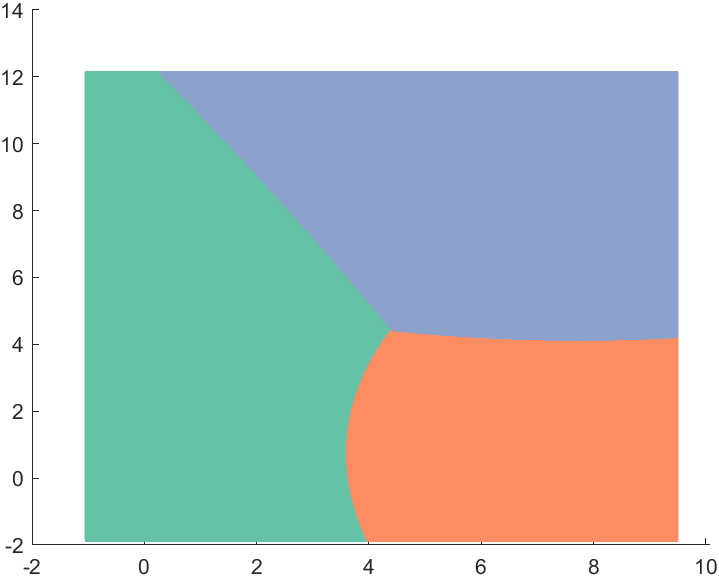
方法二：
假如没安装以上工具箱，可以使用surf函数绘制：

% 绘制聚类区域方法二
RGrid=zeros(size(x1G(:)));
GGrid=zeros(size(x1G(:)));
BGrid=zeros(size(x1G(:)));
for i=1:K
    RGrid(idx2Region==i)=colorList(i,1);
    GGrid(idx2Region==i)=colorList(i,2);
    BGrid(idx2Region==i)=colorList(i,3);
end
CGrid=[];
CGrid(:,:,1)=reshape(RGrid,size(x1G));
CGrid(:,:,2)=reshape(GGrid,size(x1G));
CGrid(:,:,3)=reshape(BGrid,size(x1G));
surf(x1G,x2G,zeros(size(x1G)),'CData',CGrid,'EdgeColor','none')
1
2
3
4
5
6
7
8
9
10
11
12
13
14

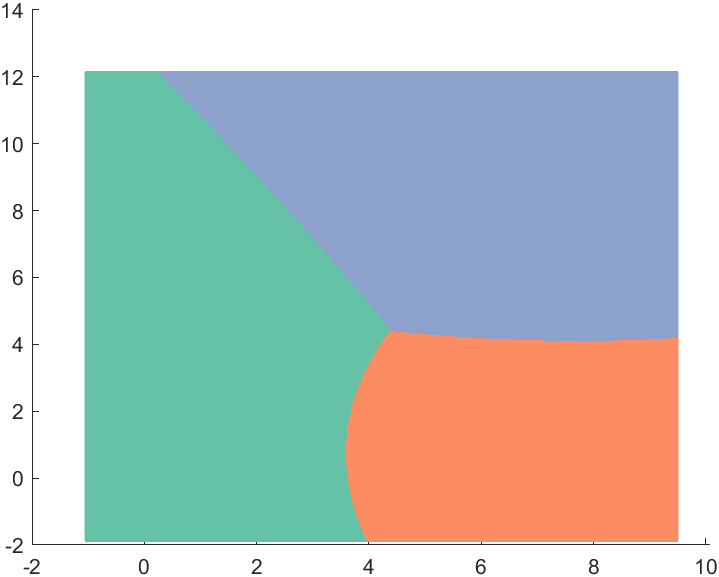
当然可以设置FaceAlpha为0.5将其变成半透明：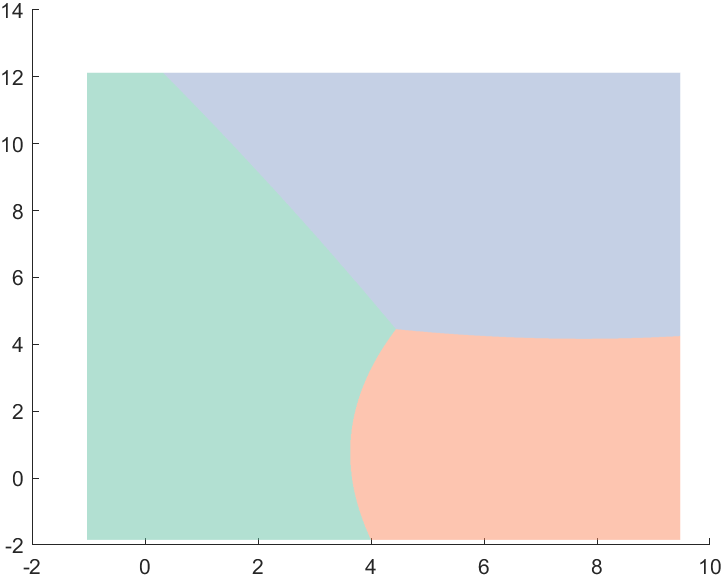

2.3 聚类边界绘制

没找到啥更好的方法，通过绘制等高线的方式绘制：

% 绘制边缘线
contour(x1G,x2G,reshape(idx2Region,size(x1G)),1.5:1:K,...
    'LineWidth',1.5,'LineColor',[0,0,0],'LineStyle','--')
1
2
3

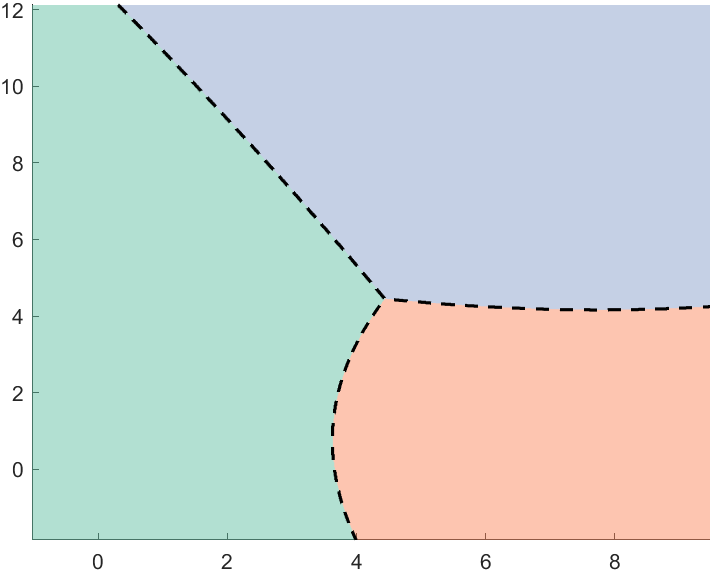
如果格点取得越密集则越精细，格点取得不太精细的话绘图放的非常大是这样：

2.4 修饰

稍微修饰一下：

% -------------------------------------------------------------------------
% 绘制聚类区域及边界
figure()
hold on
% 构造细密网格
x1=min(X(:,1)):0.01:max(X(:,1));
x2=min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G]=meshgrid(x1,x2);
XGrid=[x1G(:),x2G(:)];

% 检测每个格点属于哪一类
XV=zeros(size(XGrid,1),K);
for i=1:K
    tf=getGaussFunc(Mu(i,:),Sigma(:,:,i),Pi(i));
    XV(:,i)=tf(x1G(:),x2G(:));
end 
[~,idx2Region]=max(XV,[],2);

% 绘制聚类区域方法一
% gscatter(XGrid(:,1),XGrid(:,2),idx2Region,colorList,'..');

% 绘制聚类区域方法二
RGrid=zeros(size(x1G(:)));
GGrid=zeros(size(x1G(:)));
BGrid=zeros(size(x1G(:)));
for i=1:K
    RGrid(idx2Region==i)=colorList(i,1);
    GGrid(idx2Region==i)=colorList(i,2);
    BGrid(idx2Region==i)=colorList(i,3);
end
CGrid=[];
CGrid(:,:,1)=reshape(RGrid,size(x1G));
CGrid(:,:,2)=reshape(GGrid,size(x1G));
CGrid(:,:,3)=reshape(BGrid,size(x1G));
surf(x1G,x2G,zeros(size(x1G)),'CData',CGrid,'EdgeColor','none','FaceAlpha',.5)

% 绘制边缘线
contour(x1G,x2G,reshape(idx2Region,size(x1G)),1.5:1:K,...
    'LineWidth',1.5,'LineColor',[0,0,0],'LineStyle','--')


scatterSet=[];
strSet{K}='';
for i=1:K
    scatterSet(i)=scatter(Mu(i,1),Mu(i,2),80,'filled','o','MarkerFaceColor',...
        colorList(i,:),'MarkerEdgeColor',[0,0,0],'LineWidth',1,'LineWidth',1.9);
    strSet{i}=['Cluster center ',num2str(i)];
end
% 添加图例
legend(scatterSet,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=13;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

---

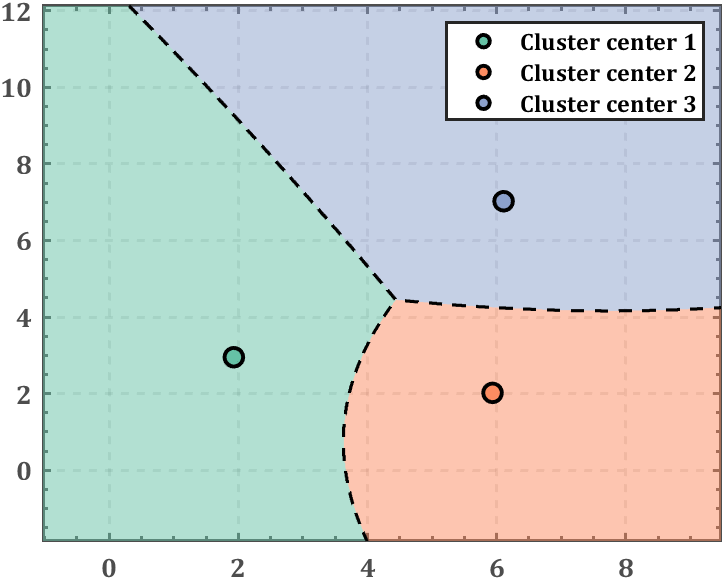
3 完整代码

% 构造三个符合高斯分布的点集并合并
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([6 2],[1 0;0 1],500);
X=[PntSet1;PntSet2;PntSet3];

% 分类数量
K=3;

% 构造GMM模型
tic
[Mu,Sigma,Pi,Class]=gaussKMeans(X,K,'dis');
toc

% 配色
colorList=[0.4  0.76 0.65
           0.99 0.55 0.38 
           0.55 0.63 0.80
           0.23 0.49 0.71
           0.95 0.57 0.47
           0.94 0.65 0.12
           0.70 0.26 0.42
           0.86 0.82 0.11];

% -------------------------------------------------------------------------
% 绘制聚类情况
figure()
hold on
strSet{K}='';
for i=1:K
    scatter(X(Class==i,1),X(Class==i,2),80,'filled',...
        'LineWidth',1,'MarkerEdgeColor',[1 1 1]*.3,'MarkerFaceColor',colorList(i,:));
    strSet{i}=['pointSet',num2str(i)];
end
legend(gca,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=13;
 
% -------------------------------------------------------------------------
% 绘制聚类区域及边界
figure()
hold on
% 构造细密网格
x1=min(X(:,1)):0.01:max(X(:,1));
x2=min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G]=meshgrid(x1,x2);
XGrid=[x1G(:),x2G(:)];

% 检测每个格点属于哪一类
XV=zeros(size(XGrid,1),K);
for i=1:K
    tf=getGaussFunc(Mu(i,:),Sigma(:,:,i),Pi(i));
    XV(:,i)=tf(x1G(:),x2G(:));
end 
[~,idx2Region]=max(XV,[],2);

% 绘制聚类区域方法一
% gscatter(XGrid(:,1),XGrid(:,2),idx2Region,colorList,'..');

% 绘制聚类区域方法二
RGrid=zeros(size(x1G(:)));
GGrid=zeros(size(x1G(:)));
BGrid=zeros(size(x1G(:)));
for i=1:K
    RGrid(idx2Region==i)=colorList(i,1);
    GGrid(idx2Region==i)=colorList(i,2);
    BGrid(idx2Region==i)=colorList(i,3);
end
CGrid=[];
CGrid(:,:,1)=reshape(RGrid,size(x1G));
CGrid(:,:,2)=reshape(GGrid,size(x1G));
CGrid(:,:,3)=reshape(BGrid,size(x1G));
surf(x1G,x2G,zeros(size(x1G)),'CData',CGrid,'EdgeColor','none','FaceAlpha',.5)

% 绘制边缘线
contour(x1G,x2G,reshape(idx2Region,size(x1G)),1.5:1:K,...
    'LineWidth',1.5,'LineColor',[0,0,0],'LineStyle','--')


scatterSet=[];
strSet{K}='';
for i=1:K
    scatterSet(i)=scatter(Mu(i,1),Mu(i,2),80,'filled','o','MarkerFaceColor',...
        colorList(i,:),'MarkerEdgeColor',[0,0,0],'LineWidth',1,'LineWidth',1.9);
    strSet{i}=['Cluster center ',num2str(i)];
end
% 添加图例
legend(scatterSet,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=13;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

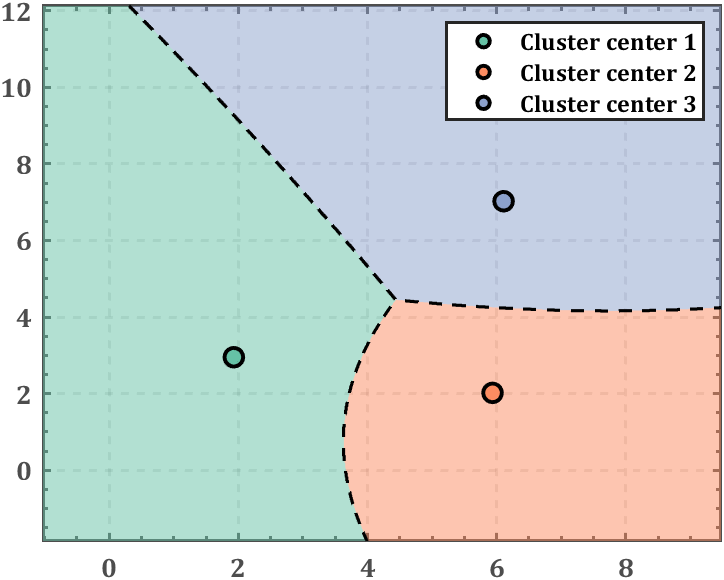
再比如将K聚类簇数量改为4:

---

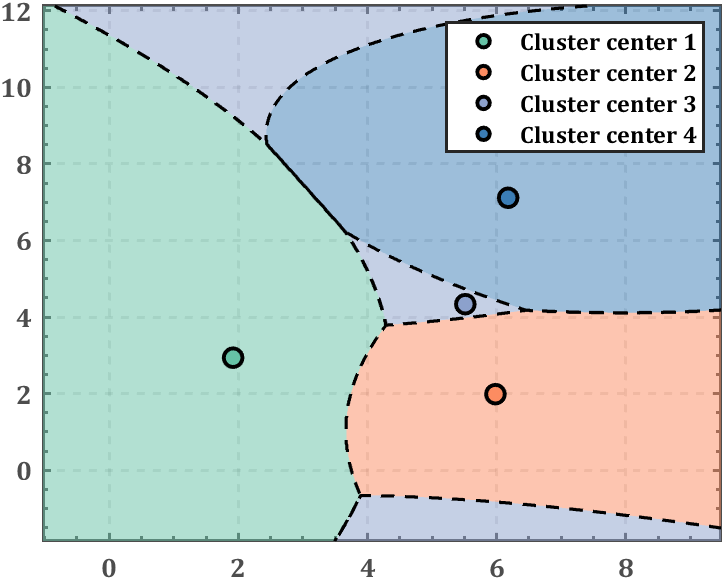
需要把全部工具函数放在一个文件夹，若是不会组装，可直接从以下链接获取文件:
链接：https://pan.baidu.com/s/18pcYK1HKgQ49Qj1uGEdG-A?pwd=slan
提取码：slan