机器学习（三）：多项式回归

如果您的数据点显然不适合线性回归（穿过数据点之间的直线），那么多项式回归可能是理想的选择。它的出现就是为了弥补线性回归。

像线性回归一样，多项式回归使用变量 x 和 y 之间的关系来找到绘制数据点线的最佳方法。

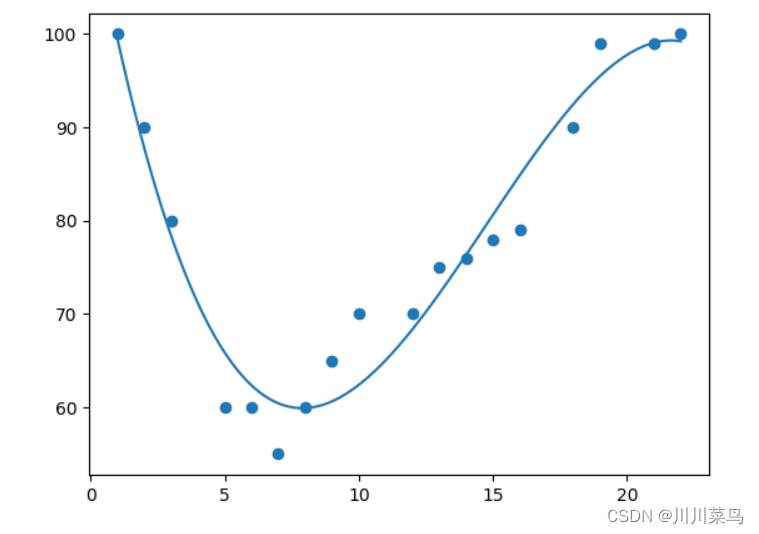
概念

研究一个因变量（目标变量）与一个或多个自变量间多项式的回归分析方法，称为多项式回归（Polynomial Regression）。如果自变量只有一个时，称为一元多项式回归；如果自变量有多个时，称为多元多项式回归。在一元回归分析中，如果因变量 y与自变量x的关系为非线性的，但是又找不到适当的** 函数曲线 ** 来拟合，则可以采用一元多项式回归。

一般来说我们用到的一元多项式模型更多，如下：

多项式回归的最大优点就是可以通过增加x的高次项对实测点进行逼近，直至满意为止，但是缺点就是如果数据太多需要耗更多时间。事实上，多项式回归可以处理相当