第二十一次CCF计算机软件能力认证

1、期末预测之安全指数

ACwing 3297

#include 
#include 
using namespace std;

typedef long long LL;

int n;
LL sum;

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        int w, c;
        scanf("%d%d", &w, &c);
        sum += (LL) w * c;
    }
    printf("%lld\n", max(sum, (LL) 0));
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2、期末预测之最佳阈值

#include 
#include 
using namespace std;

#define x first
#define y second

typedef pair<int, int> PII;
const int N = 1e5 + 10;

int n;
PII p[N];
int s[N], tmp[N];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d%d", &p[i].x, &p[i].y);
    sort(p + 1, p + n + 1);
    for (int i = 1; i <= n; i++) tmp[i] = p[i].x;
    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + p[i].y;
    int maxn = 0, res = 0;
    for (int i = 1; i <= n; i++) {
        int j = lower_bound(tmp + 1, tmp + i + 1, p[i].x) - tmp;
        int sum = s[n] - s[j - 1] + j - 1 - s[j - 1];
        if (sum >= maxn) maxn = sum, res = p[i].x;
    }
    printf("%d\n", res);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3、带配额的文件系统

ACwing 3299

4、食材运输(01覆盖问题、重复覆盖问题)

ACwing 3300

先考虑简单情况，假设只有一种食材，且车辆固定从树的根节点出发，走完所有需要这种食材的点，最少需要走多少时间？

考虑需要回到起点的情况，可以发现，对于每条边而言，如果其对应的子树中如果包含需要该种食材的点，车辆就一定会往下走，由于要回去，因此该边至少要走两次，因此就可以得出该方式的时间下限：每条边「恰好」走两次，「恰好」是因为这个过程类似于树的DFS遍历过程，每条边刚好走两次。故如果需要回到起点，这种情况的「最长时间就是所有子树包含所需食材的边的长度长的两倍」。

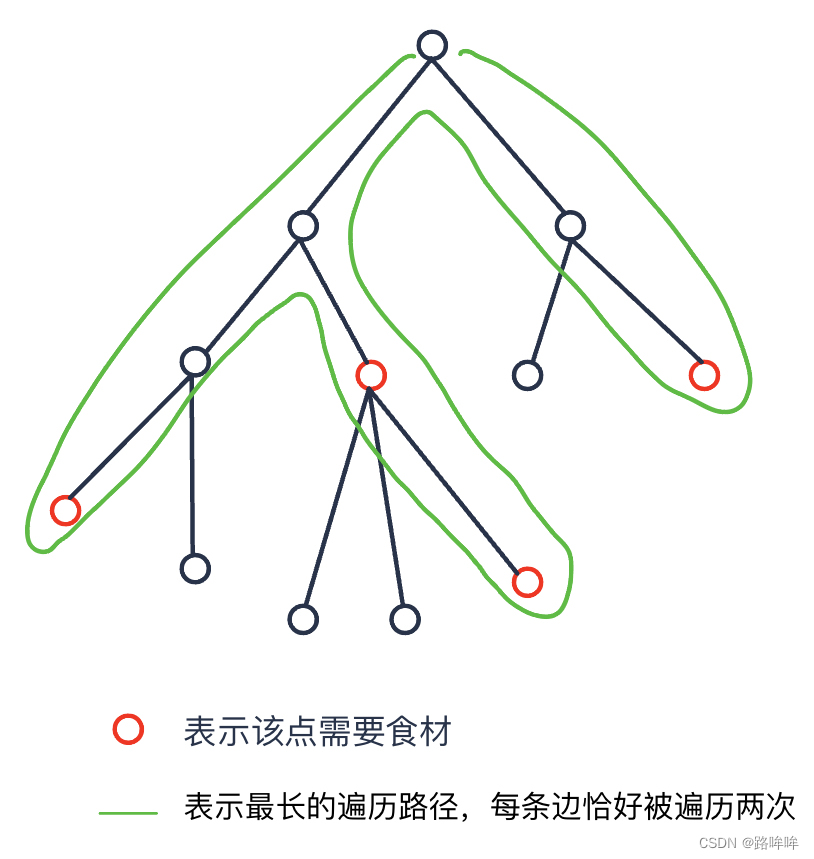
如果不需要回到起点，它的最长路径仅仅比需要回到起点的情况少去最终到达的点与根结点的距离，即有一部分边仅遍历一次。

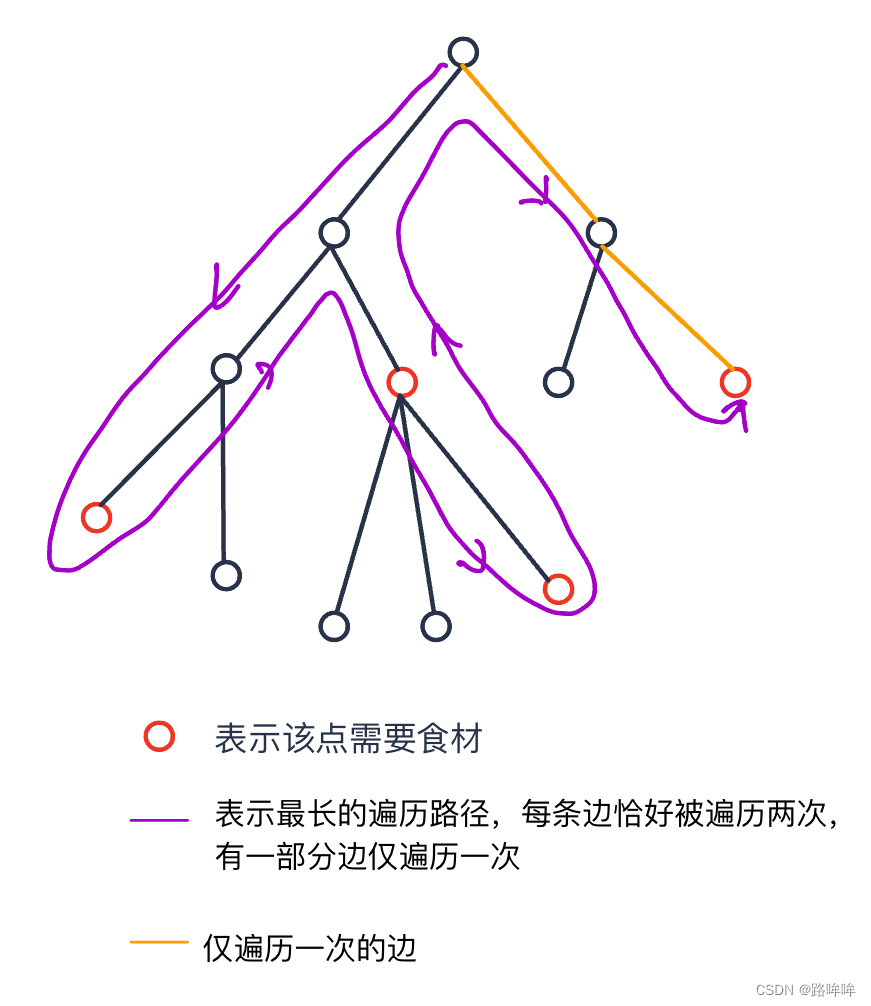
如果需要回到起点的情况下求出来的距离记为 $C$，每个点到根结点的距离记为 $d[i]$。因此对于第 $k$ 个结点，对于不回到起点的遍历情况，终点为 $k$ 的遍历路径长度为 $$S=C-d[k]$$由于 $C$ 固定，为了使 $S$ 尽可能小，就需要选择 $d[k]$ 尽可能大的点作为终点，即「距离根结点更远的点」。

从上面的分析可以得出，在只有一种食材、且必须从起点出发的前提下，能够预先处理出遍历完所有需要食材的点所需时间。

预处理： $d[i][j]$ 表示从 $i$ 点出发走完所有包含食材的点 $j$ 的最短距离。

后面问题为：从 $n$ 个点中最多选择 $M$ 个点，从中选择 $k$ 个点来作为 $k$ 辆车的起点，在 $k$ 种食材都满足的条件下，所有路径的最大值最小的值。

考虑二分，首先二分出来一个距离 $mid$，对于 $k$ 种食材，使用 $0$ 和 $1$ 来表从该点出发每一种食材是否能够满足(即所有需要该种食材的点都能遍历到)，如果 $d[i][j]<=mid$，则该种食材值设置为 $1$，否则为 $0$，即可得出类似于如下 $n\times k$ 的矩形。

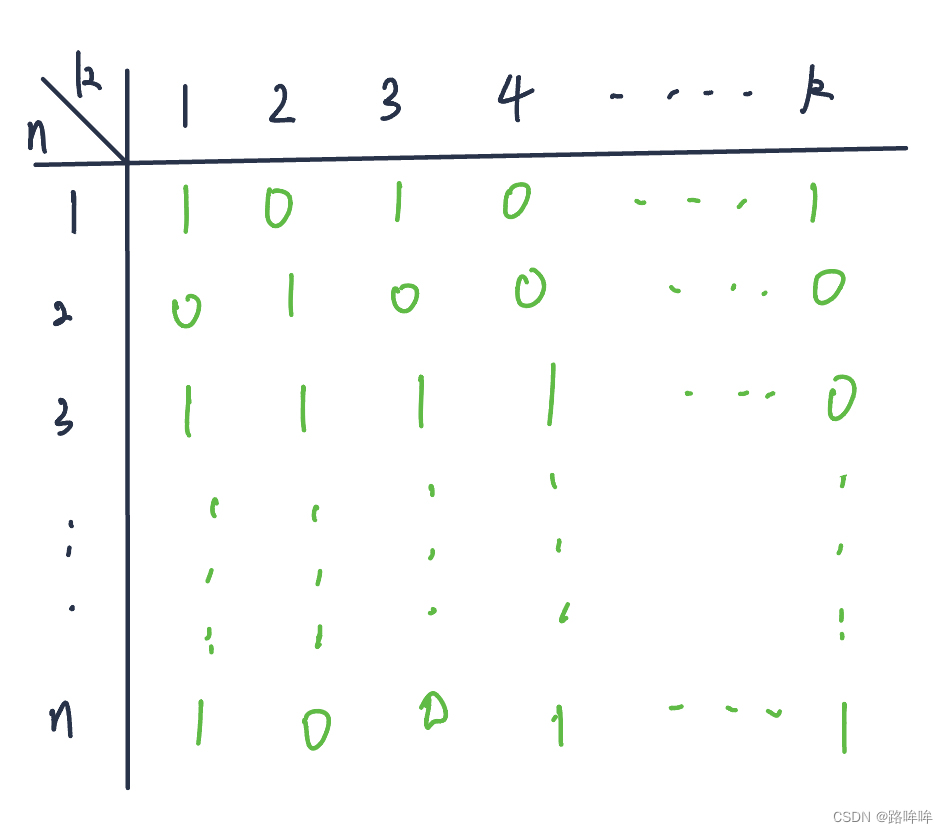
上图中，横向表示 $k$ 种食材，纵向表示 $n$ 个点，其中 $0$ 和 $1$ 表示在最多 $mid$ 距离前提下，从第 $i(i\in [1,n])$ 个点出发是否能到达所有需要第 $j(j\in [1,k])$ 种食材的点。

现在问题是在 $n$ 个点中最多选择 $M$ 个点作为起点使得 $k$ 种食材都能够满足前提下，最少选择多少行，使得选择出来的 $01$ 矩阵的每一列中都至少包含一个 $1$，即对每一列分别求按位或 $|$ ，最终每一列的值都是 $1$。

这就转换为了经典的「01覆盖问题」或者「重复覆盖问题」，其通用解法为 $DanceLinks$，在列数不多情况下可以使用「状态压缩DP」，参考ACwing 524.愤怒的小鸟。

#include 
#include 
#include 
using namespace std;

#define x first
#define y second

typedef pair<int, int> PII;
const int N = 110, M = 10, S = 1 << M;

int n, m, k;
int need[N][M]; // 每个点需要哪些食材
int h[N], e[N * 2], w[N * 2], ne[N * 2], idx;
int d[N][M]; // 预处理结果
int f[S], state[N]; // state表示第i行有哪些列为1

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// u当前结点 fa父结点 v第v种食材
PII dfs(int u, int fa, int v) {
    PII res(0, -1);
    if (need[u][v]) res.y = 0;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa) continue;
        auto t = dfs(j, u, v);
        if (t.y != -1) {
            res.x += t.x + w[i] * 2;
            res.y = max(res.y, t.y + w[i]);
        }
    }
    return res;
}

bool check(int mid) {
    memset(state, 0, sizeof state);
    for (int i = 1; i <= n; i++)
        for (int j = 0; j < k; j++)
            if (d[i][j] <= mid) state[i] |= 1 << j;
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    for (int i = 0; i < 1 << k; i++)
        for (int j = 1; j <= n; j++)
            f[i | state[j]] = min(f[i | state[j]], f[i] + 1);
    return f[(1 << k) - 1] <= m;
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 1; i <= n; i++)
        for (int j = 0; j < k; j++)
            cin >> need[i][j];
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c; scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    for (int i = 1; i <= n; i++)
        for (int j = 0; j < k; j++) {
            // 返回两个值：关键边的两倍 和 距离第i个点最远的被标记的点
            auto t = dfs(i, -1, j);
            if (t.y != -1) d[i][j] = t.x - t.y;
        }
    int l = 0, r = 2e8; // 边权最大1e6，有100个点，路径最大长度1e8，两倍路径长度最大2e8
    while (l < r) {
        int mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%d\n", r);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75