LeetCode 热题 HOT 100 第七十四天 337. 打家劫舍 III 中等题 用python3求解

题目地址

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。
除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:
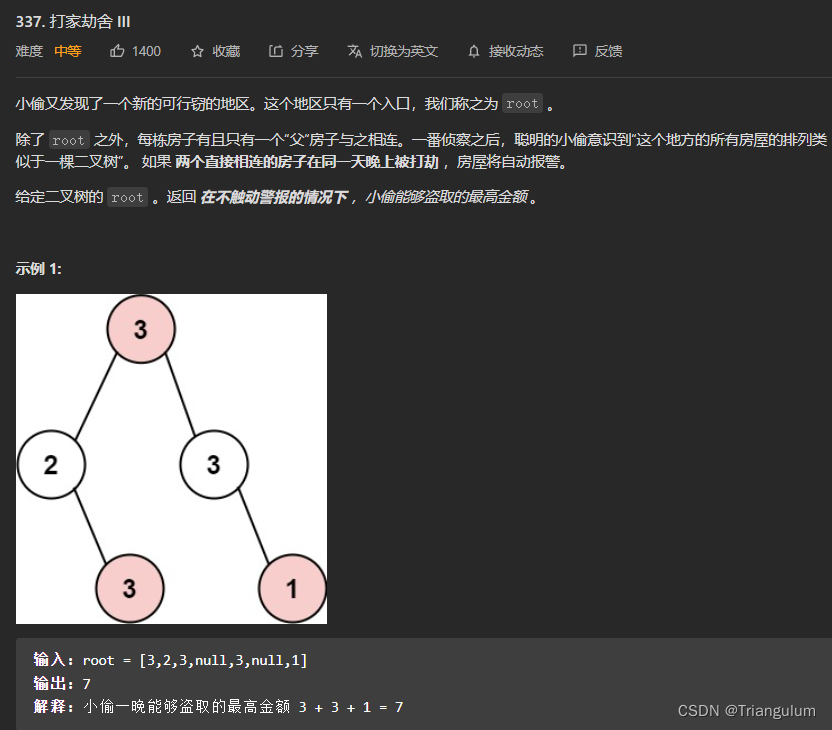
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:
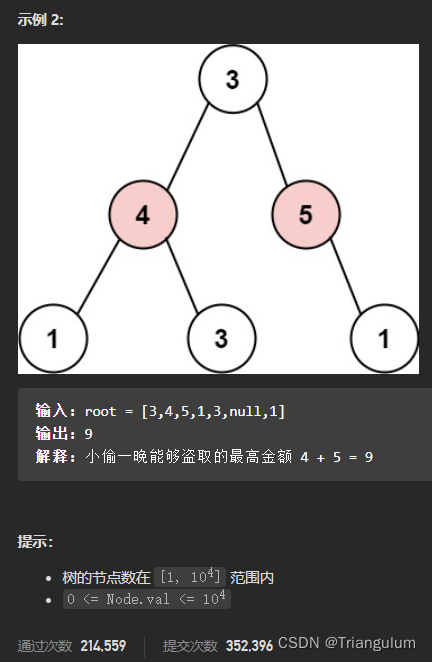
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：
树的节点数在 [1, 10^4] 范围内
0 <= Node.val <= 10^4


解法：递归（后序遍历）
后序遍历的顺序：左子树–>右子树–>根节点
递归处理，返回当前节点偷与不偷的两个结果，取其中最大的一个。

本题一看就是一个经典的DP。
难点在于，如果从上往下看这棵树，是无法在遍历到某一个节点时决定【偷或不偷】这个节点的收益的。
因此，我们要想办法从下往上看，于是就想到了后序遍历。

class Solution:
    def rob(self, root: TreeNode) -> int:
        def DFS(root):
            if not root:
                return 0, 0
            # 后序遍历
            leftchild_steal, leftchild_nosteal = DFS(root.left)
            rightchild_steal, rightchild_nosteal = DFS(root.right)

            # 偷当前node，则最大收益为【投当前节点+不偷左右子树】
            steal = root.val + leftchild_nosteal + rightchild_nosteal
            # 不偷当前node，则可以偷左右子树
            nosteal = max(leftchild_steal, leftchild_nosteal) + max(rightchild_steal, rightchild_nosteal)
            return steal, nosteal
            
        return max(DFS(root))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16