链表经典题带刷(内含精华：链表深拷贝)

目录

链表的回文判断

题目描述

解题逻辑

代码实现

相交链表

题目描述

解题逻辑 

 代码实现

环形链表判断

题目描述

解题逻辑

 代码实现

环形链表进阶版

题目描述

解题逻辑

丐版：

升级版

代码实现

丐版

 升级版

复制带随机指针的链表

问题描述

解题逻辑 

平民版：

贵族版：

代码实现

平民版：

贵族版：

链表的回文判断

题目描述

对于一个链表，请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法，判断其是否为回文结构。

给定一个链表的头指针A，请返回一个bool值，代表其是否为回文结构。保证链表长度小于等于900。

解题逻辑

这道题有些大佬把链表中的数据拷贝到了数组上再处理，跑过了，当然，如果在面试敢那么写也是真的勇士。

普通的解题思路就有些朴实无华且枯燥了：

第一步：利用快慢指针得到中间指针的位置。

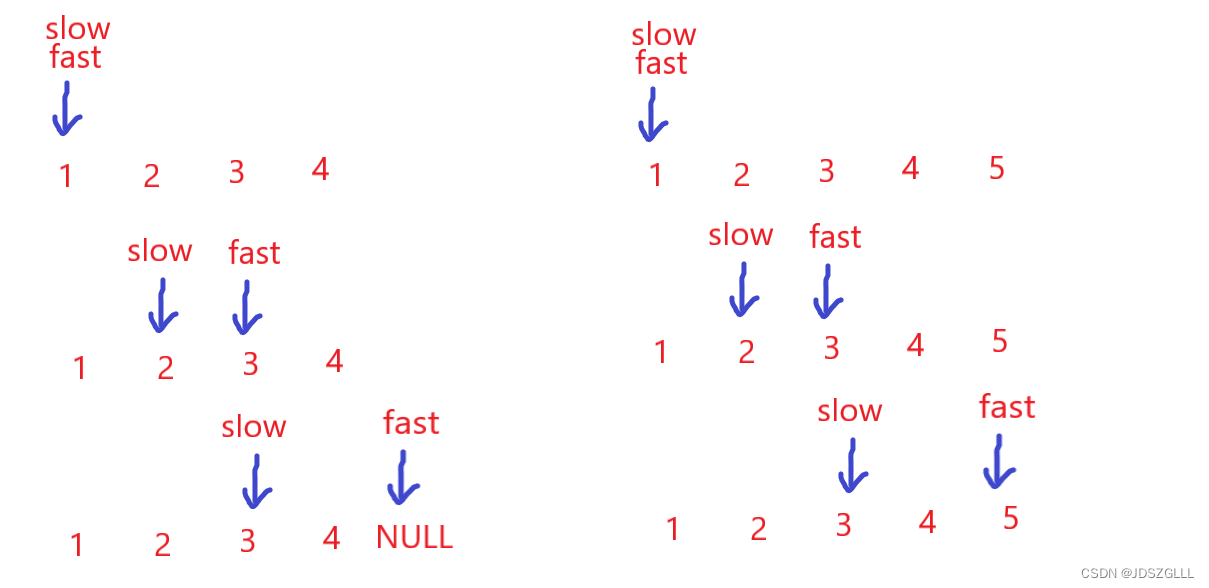
我们可以看到，慢指针走一步，快指针走两步，最后得到中间指针。

第二步：逆置中间指针之后的链表。

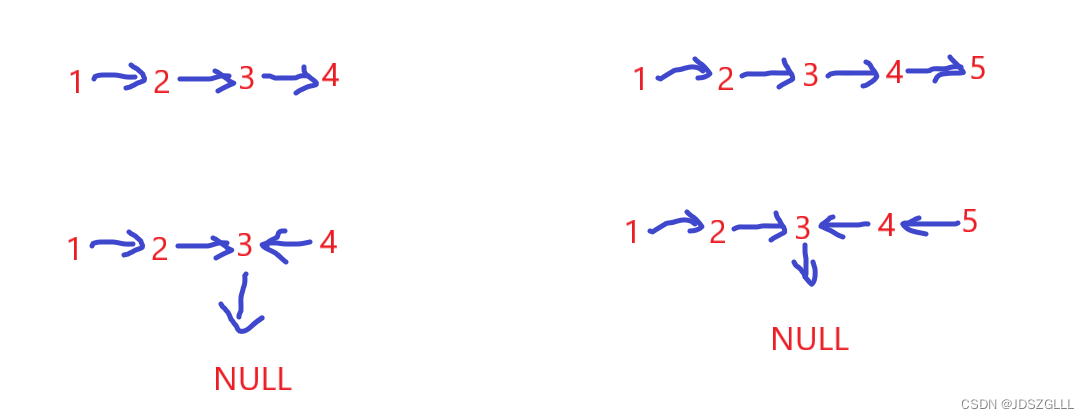
这时候我们的重构已经完成了。

第三步：比较两个新的链表的元素是否相同。

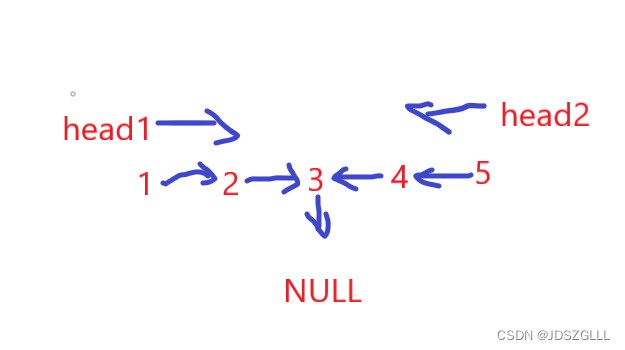
 从图中可以看出，从head1和head2开始，比较两个链表从头到尾的元素是否相同，如果相同就是回文。

代码实现

bool chkPalindrome(ListNode* A)
{
        //排除0个和1个元素的情况
        if(A == NULL || A->next == NULL)
            return true;
 
        //第一步找到中间节点
        ListNode* fast = A;
        ListNode* slow = A;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
        }
 
        //第二步逆置后半段
        ListNode* prev = slow;
        ListNode* cur = slow->next;
        while(cur)
        {
            ListNode* back = cur->next;
            cur->next = prev;
            prev = cur;
            cur = back;
        }
        slow->next = NULL;
 
        //第三步，比较两个链表
        ListNode* cur1 = A;
        ListNode* cur2 = prev;
        while(cur1 && cur2)
        {
            if(cur1->val != cur2->val)
            {
                return false;
            }
            cur1 = cur1->next;
            cur2 = cur2->next;
        }
        return true;
}

相交链表

题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

如图所示，如果是相交链表，返回的应该是C节点的地址。

解题逻辑 

第一步：从headA和headB开始遍历，分别求出两个链表的长度，并且比较尾节点是否是同一个节点，如果是同一个则是交叉链表，如果尾节点不是同一个，则不构成交叉链表，返回NULL。

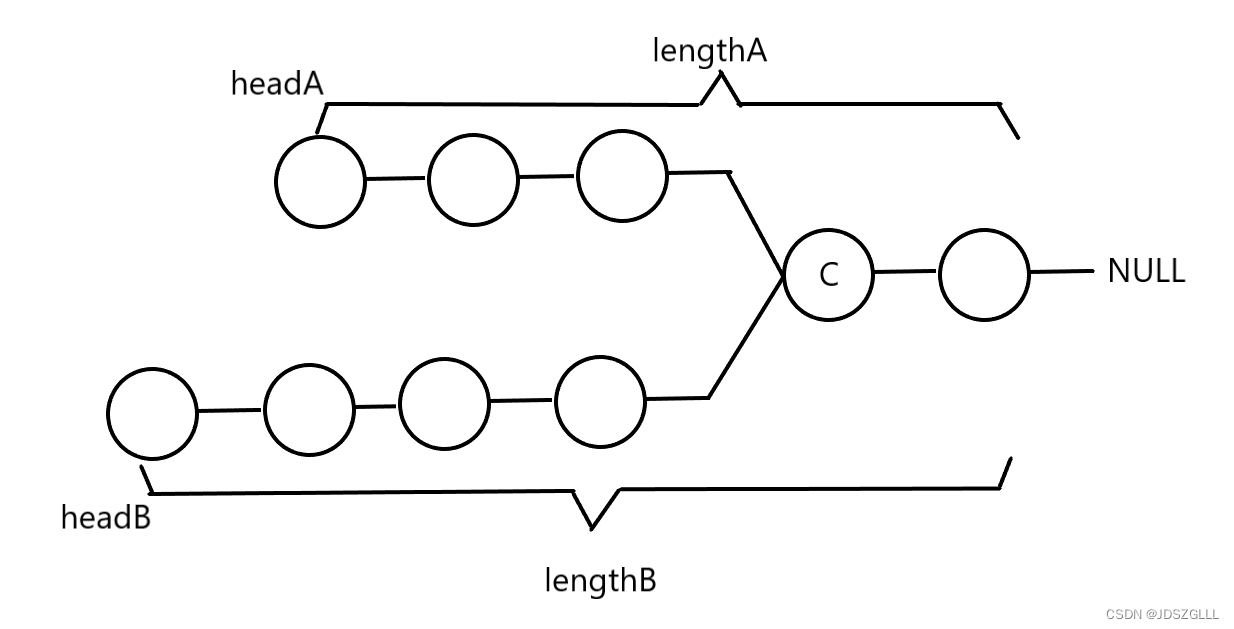
第二步：两个指针都从头开始走，但是较长的链表的遍历指针先走两个长度的差值步（lengthA - lengthB的绝对值）， 然后开始比较两个指针所指向的地址是否相同，一旦相同，则返回相应的地址。

 代码实现

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    //第一步
    if(headA == NULL || headB == NULL)
    {
        return NULL;
    }
    struct ListNode *cur_A = headA;
    struct ListNode *cur_B = headB;
    int length_A = 1;
    int length_B = 1;
    while(cur_A->next)
    {
        ++length_A;
        cur_A = cur_A->next;
    }
    while(cur_B->next)
    {
        ++length_B;
        cur_B = cur_B->next;
    }
    if(cur_A != cur_B)
    {
        return NULL;
    }
 
    //第二步
    struct ListNode * longest_head = headA;
    struct ListNode * shortest_head = headB;
    if(length_A < length_B)
    {
        longest_head = headB;
        shortest_head = headA;
    }
    for(int i = 0; i < abs(length_B - length_A); i++)
    {
        longest_head = longest_head->next;
    }
    while(longest_head != shortest_head)
    {
        longest_head = longest_head->next;
        shortest_head = shortest_head->next;
    }
    return longest_head;
}

环形链表判断

题目描述

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false。

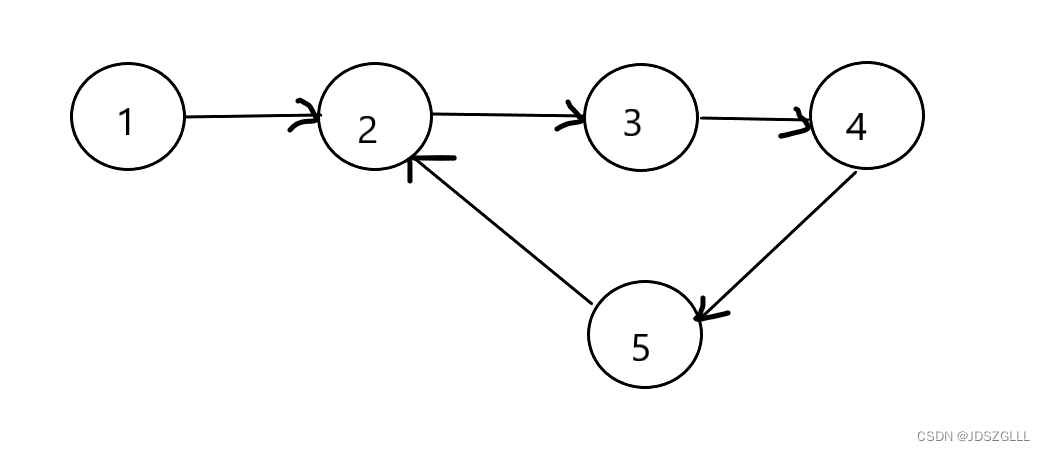
如图所示，链表中尾节点的next链接到第二个节点，带环，返回true。

解题逻辑

这道题可以使用双指针法解决，一快一慢，快指针一次走两步，慢指针一次走一步，如果链表不带环，快指针会先走到空，自然返回false，如果在指针移动过程中，慢指针赶上了快指针，这说明链表带环。

 代码实现

bool hasCycle(struct ListNode *head) 
{
    struct ListNode *fast = head;
    struct ListNode *slow = head;
 
    while(fast != NULL && fast->next != NULL)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        {
            return true;//追上了
        }
    }
 
    return false;//走到头了
}

环形链表进阶版

题目描述

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

也就是在第一题判断一个链表是不是环形链表的基础上，还要找到链表尾链接到的节点的位置（从0开始计算）。

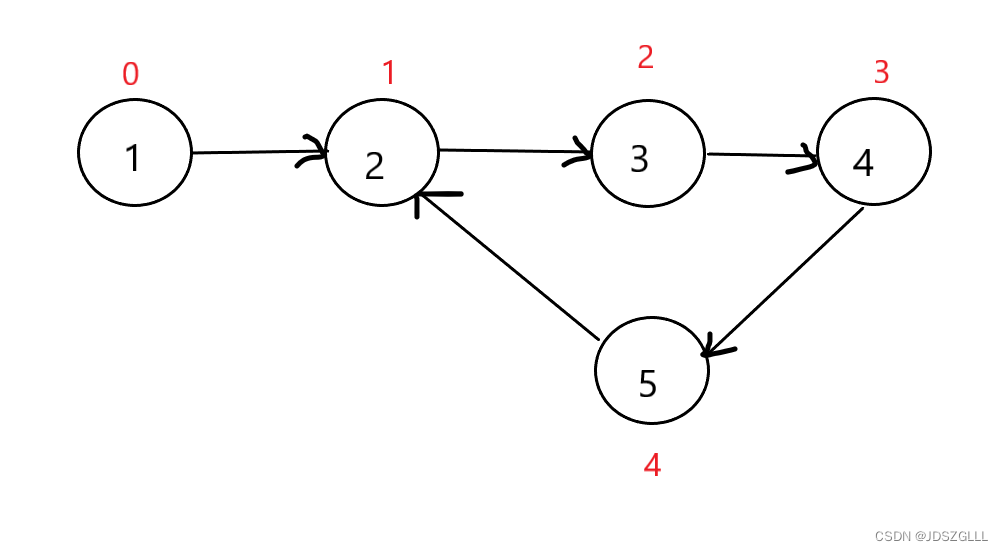
解题逻辑

 这道题可以分为两步，第一步是判断这个链表到底是不是带环链表，如果不是，都不用进入第二步，直接返回-1，如果是带环链表，则进入下一步。

让我们直接快进到快慢指针相遇的那一刻。

第二步有两种解题思路，接下来我们分别讲解：

丐版：

我们把带环链表构造成交叉链表，以原来的头节点作为head1,相遇节点的后一个节点作为head2，这样我们就可以用第二题的方法来解决第二步了。

但是，要知道第二题的解题方法还是有些繁琐的，在求交叉节点位置之前，还要求得两条链表的长度。

升级版

第二种的方法则用到了数学推导的方法，让我们来看看：

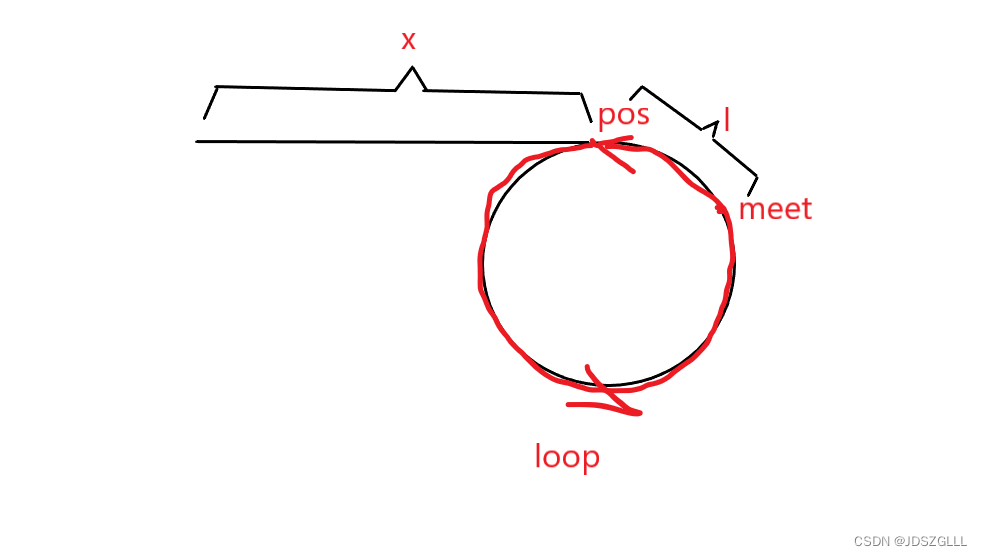
我们设：头节点head到入环节点POS的步数为X，入环节点POS到相遇节点meet的步数为l，绕环一圈要走的步数为loop；

慢指针走过的步数为l + x;

快指针走过的步数为l + x + loop。

因为慢指针走一步，快指针走两步，所以 2 * (l + x) = l + x + loop;

两边化简一下，得到 l + x = loop;

再调整一下得到 l = loop - x。

也就是说，两个指针，一个从头节点head出发，一个从相遇节点meet出发，走过l(l = loop - x)步，会在入环节点处相遇。

代码实现

丐版

//找到交叉链表的交叉节点
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    if(headA == NULL || headB == NULL)
    {
        return NULL;
    }
    struct ListNode *cur_A = headA;
    struct ListNode *cur_B = headB;
    int length_A = 1;
    int length_B = 1;
    while(cur_A->next)
    {
        ++length_A;
        cur_A = cur_A->next;
    }
    while(cur_B->next)
    {
        ++length_B;
        cur_B = cur_B->next;
    }
    if(cur_A != cur_B)
    {
        return NULL;
    }
    struct ListNode * longest_head = headA;
    struct ListNode * shortest_head = headB;
    if(length_A < length_B)
    {
        longest_head = headB;
        shortest_head = headA;
    }
    for(int i = 0; i < abs(length_B - length_A); i++)
    {
        longest_head = longest_head->next;
    }
    while(longest_head != shortest_head)
    {
        longest_head = longest_head->next;
        shortest_head = shortest_head->next;
    }
    return longest_head;
}
 
 
//返回带环链表开始入环的第一个节点
struct ListNode *detectCycle(struct ListNode *head) 
{
    //第一步，判断是不是带环链表
    struct ListNode *fast = head;
    struct ListNode *slow = head;
    if(head == NULL || head->next == NULL)
        return NULL;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == NULL || fast->next == NULL)//走到尽头，不是带环链表
        {
            return NULL;
        }
        if(fast == slow)//快指针追上慢指针
        {
            break;
        }
    }
 
    //构建交叉链表
    struct ListNode * meet = slow;
    struct ListNode * head1 = head;
    struct ListNode * head2 = meet->next;
    meet->next = NULL;
 
    //获得入环节点，并把链表复原
    struct ListNode * ret = getIntersectionNode(head1, head2);
    meet->next = head2;
    return ret;   
}

我们可以看到，把寻找交叉链表的交叉节点的步骤加上，多出来一大堆代码，显然这个方法不太方便。

 升级版

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *fast = head;
    struct ListNode *slow = head;
    if(head == NULL || head->next == NULL)
        return NULL;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == NULL || fast->next == NULL)
        {
            return NULL;
        }
        if(fast == slow)
        {
            break;
        }
    }
    slow = head;
    while(slow != fast)
    {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;   
}

明显感觉到，第二种方法的代码简洁了许多，第一种的优势是思路比较简单，第二种方法要进行一定的推导，两种方法各有千秋，还是看自己如何取舍。

复制带随机指针的链表

问题描述

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

 

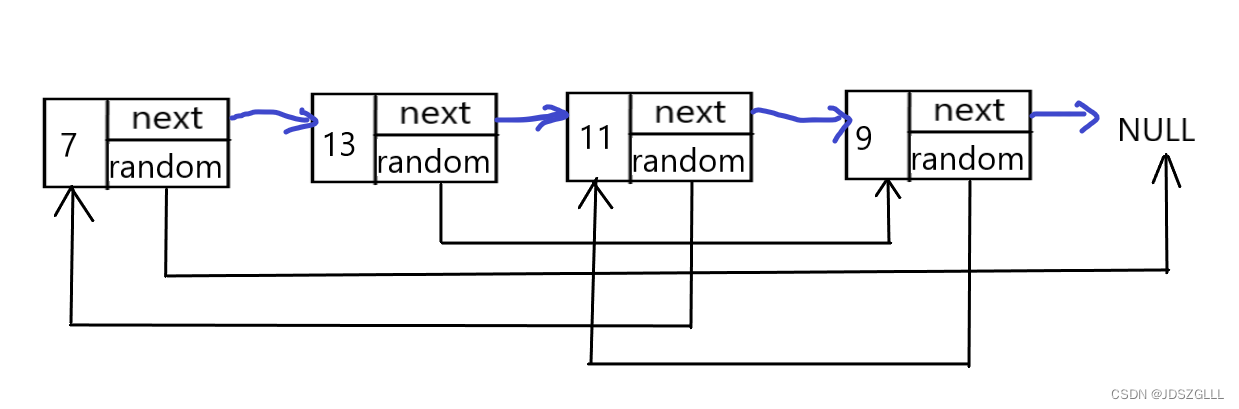
解题逻辑 

这道题的解题思路也有两种：

平民版：

第一步，忽略random指针，构建一个其他指向关系已经内容与原指针相同的链表，这一步还是很容易实现的。

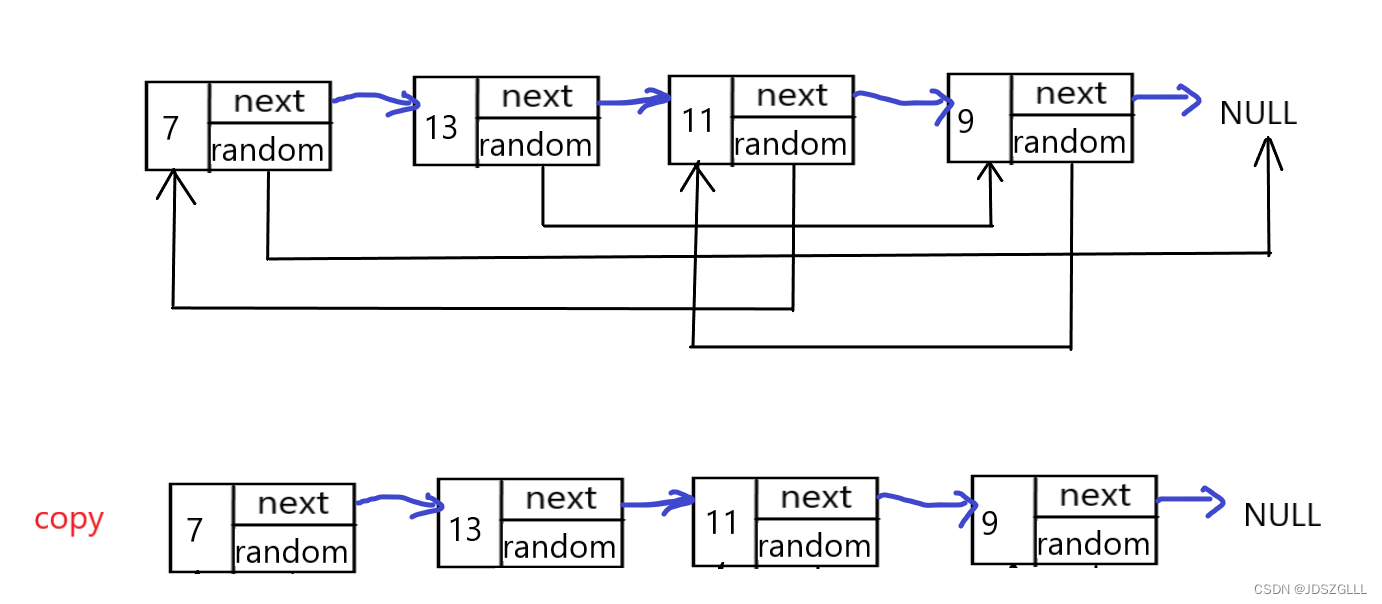
 接下来要捋清楚copy的链表的random指向何处，就要和原链表比较，从头开始遍历，指向的节点排第几位，就链接到相应节点。

我们可以清楚地看到，prev1指针遍历链表，直到遇到NULL，prev1走一步，prev2也走一步，cur1指针遍历链表找到与prev1->random相同的节点时，cur2正好也到达pre2->randow应该指向的位置，prev2（newprev）和cur2(newcur)根据原链表的关系链接。

贵族版：

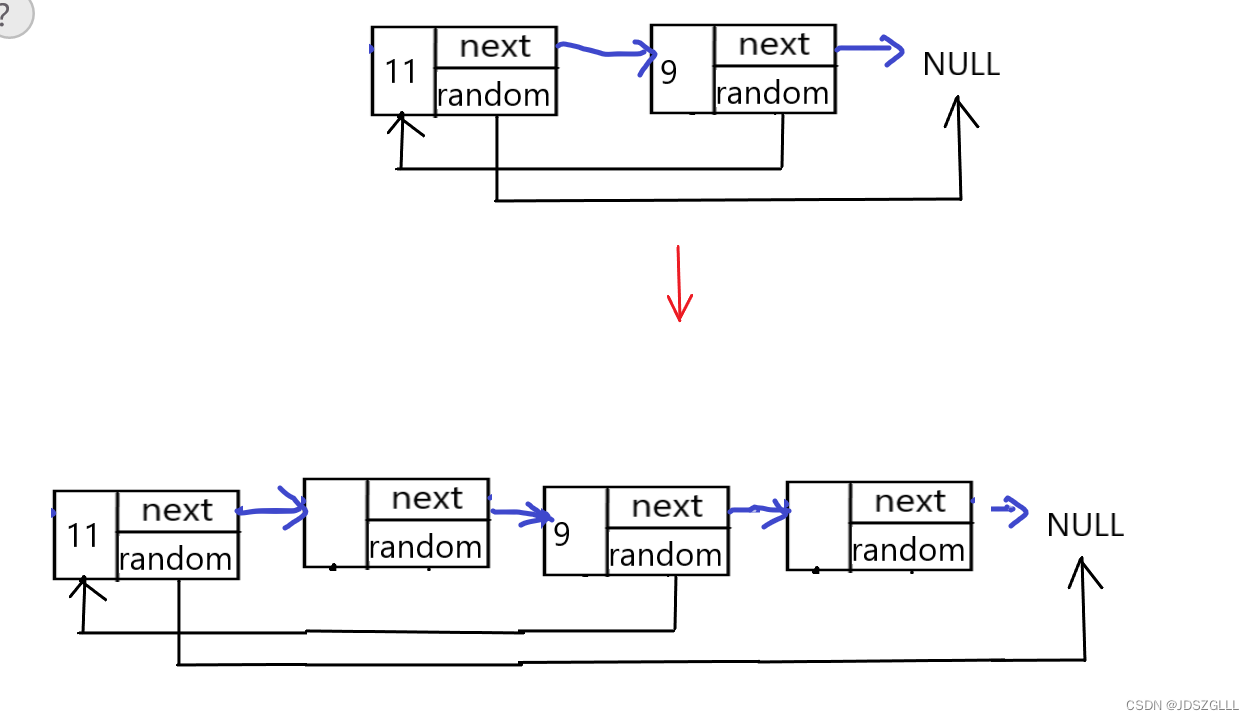
 第二种方法要一些巧思，一般来说靠自己比较难想到。我们先在原链表的每个节点之后插入一个新的节点。

 

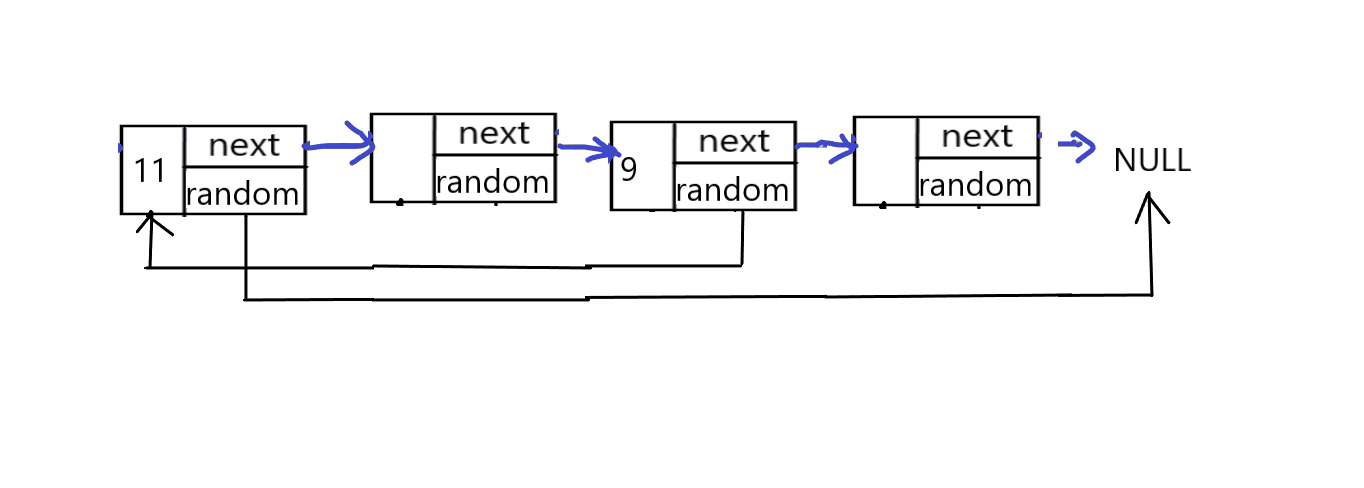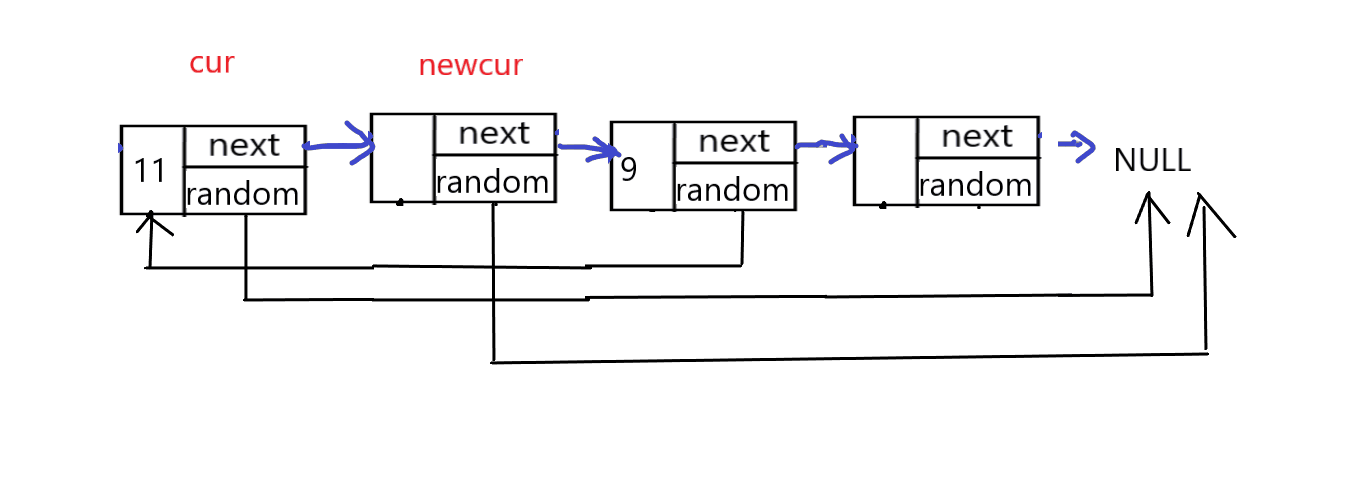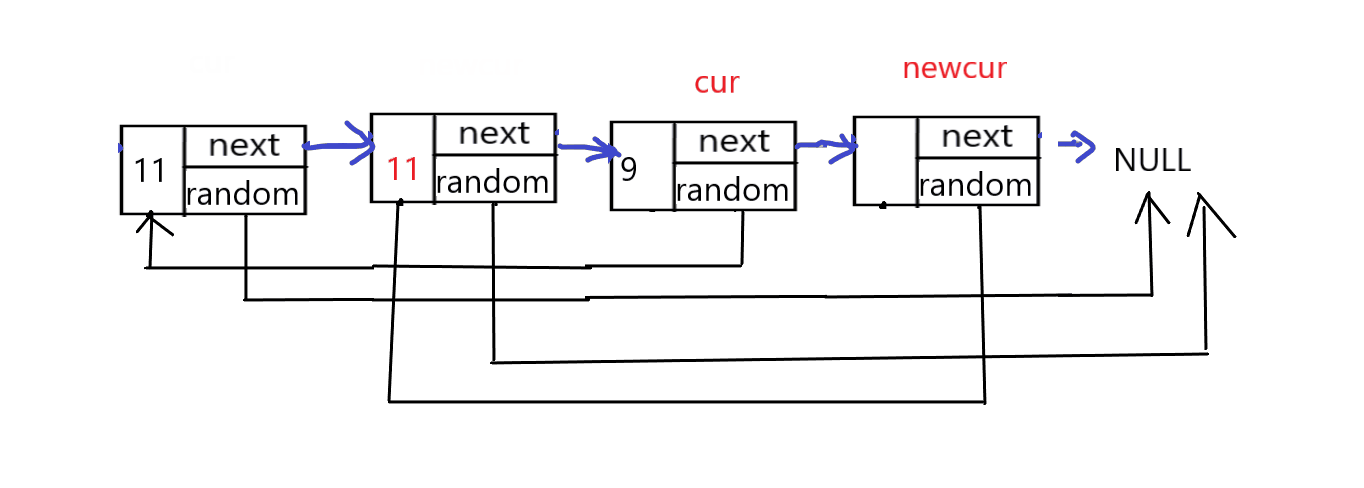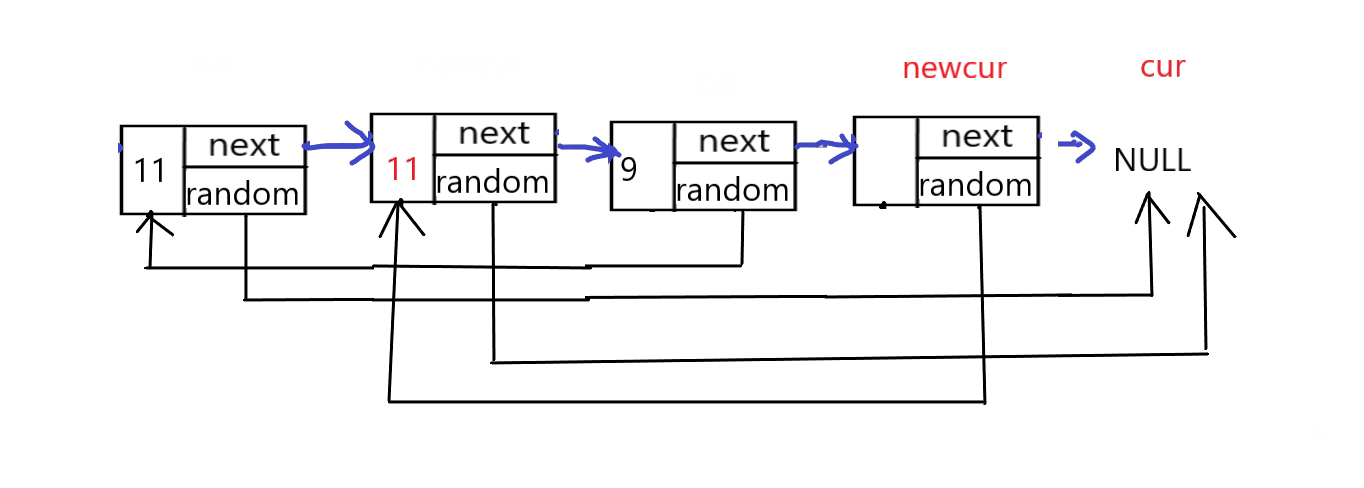
第二步，创建两个指针，cur和newcur分别指向原链表和新链表的节点，遍历链表，当原链表的cur节点的random指向非空节点时，新链表的指针newcur指针的random指向原链表cur节点的random的next节点。

最后一步，将链表复原。

代码实现

平民版：

struct Node* copyRandomList(struct Node* head) {
    if(head == NULL)
        return NULL;
 
    //复制链表
    struct Node* cur = head;
    struct Node* newprev = NULL;
    struct Node* newcur = NULL;
    struct Node* newhead = NULL;
    while(cur)
    {
        newcur = (struct Node*)malloc(sizeof(struct Node));
        if(cur == head)
        {
            newhead = newcur;
        }
        newcur->val = cur->val;
        newcur->random = cur->random;
        newcur->next = cur->next;
        if(newprev != NULL)
            newprev->next = newcur;
        newprev = newcur;
        cur = cur->next;
    }
 
    //对照原链表建立random链接
    newprev = newhead;
    while(newprev)
    {
        cur = head;
        newcur = newhead;
        while(newprev->random != cur)
        {
            cur = cur->next;
            newcur = newcur->next;
        }
        newprev->random = newcur;
        newprev = newprev->next;
    }
    return newhead;
}

贵族版：

struct Node* copyRandomList(struct Node* head) {
    if(head == NULL)
    {
        return NULL;
    }
    //在原链表之后插入节点
    struct Node* cur1 = head;
    struct Node* cur2 = NULL;
    while(cur1)
    {
        struct Node* newnode = (struct Node*)malloc(sizeof(struct Node));
        newnode->val = cur1->val;
        newnode->next = cur1->next;
        newnode->random = NULL;
        cur1->next = newnode;
        cur1 = cur1->next->next;
    }
    //建立新节点之间的联系
    cur1 = head;
    struct Node* newhead = head->next;
    while(cur1)
    {
        cur2 = cur1->next;
        if(cur1->random == NULL)
        {
            cur2->random == NULL;
        }
        else
        {
            cur2->random = cur1->random->next;
        }
        cur1 = cur1->next->next;
    }
 
    //拆分两个链表
    cur1 = head;
    while(cur1)
    {
        cur2 = cur1->next;
        cur1->next = cur2->next;
        if(cur2->next != NULL)
        {
            cur2->next = cur2->next->next;
        }
        cur1 = cur1->next;
    }
 
    return newhead;
}